自然対数も有理数で近似したい
こんにちは。対数表が使えない冪乗の比較の問題で二進対数を愛用しているNayuta Itoです。
最近はその手の問題の初手が
$3^{12} = 531441 > 524288 = 2^{19}$ より、 $\log_2{3} > \frac{19}{12}$である。
で固定されてきました。
イントロダクション
ところで私が二進対数を使用しているのは、単に$2$の冪乗が計算しやすいからです。数学の理論の上では何の優位性もなく、別に他の数字だっていいわけです。
では、数学的に最も自然な底は何でしょう。それはもちろん、自然対数の底、ネイピア数$e$ですね。
というわけで、この記事では小さい素数の自然対数を同じ分母の有理数で近似することを考え、最も都合のいい分母を探します。
以下では、底が省略された$\log$は全て自然対数を表すものとします。
$2$について考える
普段は底が$2$の対数で考えるので$2$を省略できますが、今回は$2$からきちんと考える必要があります。
$\log{2}$の連分数展開は
$$[0; 1, 2, 3, 1, 6, 3, 1, 1, \cdots]$$
なので、これを途中までで打ち切った分数を並べてみましょう。
$$1, \frac{2}{3}, \frac{7}{10}, \frac{9}{13}, \frac{61}{88}, \frac{192}{277}, \frac{253}{365}, \frac{445}{642}, \cdots$$
こう見ると、$10$か$13$が現実的なようです。
大きい素数を見てみる
$10$と$13$で、どちらが他の素数をよりよく近似できるか見てみましょう。
| $\times 10$ | $\times 13$ | |
|---|---|---|
| $\log{2}$ | $6.931$ | $9.011$ |
| $\log{3}$ | $10.986$ | $14.282$ |
| $\log{5}$ | $16.094$ | $20.923$ |
| $\log{7}$ | $19.459$ | $25.297$ |
| $\log{11}$ | $23.979$ | $31.173$ |
| $\log{13}$ | $25.649$ | $33.344$ |
| $\log{17}$ | $28.332$ | $36.832$ |
| $\log{19}$ | $29.444$ | $38.278$ |
| $\log{23}$ | $31.355$ | $40.761$ |
$10$は$2,3,5,11$でよい近似ができる一方、$13$は$3$の精度がよくないようです。
以下では、$10$を分母とした場合について考察します。
堆積
さて、$\log{2} \fallingdotseq \frac{7}{10}$がわかったので、こんな図を書きたくなります。
書かれている数字は$e^{\frac{1}{10}}$の何乗かを示すもので、時計回りに1つ進むと$2$倍、反時計回りに1つ進むと$\frac{1}{2}$倍になります。底が$e$なので、$e$倍の違いは無視しています。
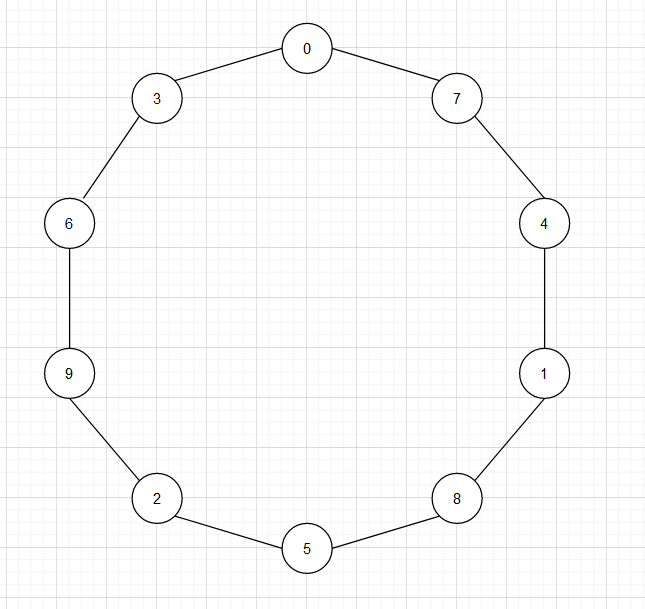The circle of doublings
$0$と$1$が近いのが気になりますが・・・仕方ないですね。
感想
指数・対数では人間の都合でしか出番のないと思っていた$10$が大活躍していたので、$10$のことを見直しました。
おまけ
何かのUIと、
何かのUI
何かの表と、
何かの表
何かの音源です。
https://soundcloud.com/nayuta-ito-521748543/5l2zzc1lnzhb
ご自由にお使いください。
