ええと、初記事です。
はじめに
はじめまして、にっくねーむと申します！
今回は自己紹介と、高2のときに(自称)見つけて以来Twitter(現$\mathbb{X}$)のヘッダーにしていた数式：
$$ (2n+1)!\sum^n_{k=0}\frac{(-1)^k{}_n\mathrm{C}_k}{n+k+1}=(n!)^2 $$
を見つけた経緯と、その組み合わせ的な解釈について書きたいと思います。
はじめての投稿ですので拙い部分も多々あると思いますが最後まで読んでくださると嬉しいです！！！
実際のTwitterのプロフ画面
自己紹介
ニックネーム：にっくねーむ
所属：東北大学文学部、作問サークル、ミステリ研究会
好きな食べ物：オムライス、チーズ系全般、寿司
ニガテな食べ物：ピーマン、ゴーヤ、梅干し、刺身こんにゃく
興味がある分野：日本近現代史(特に初期議会、元老政治)、数論、解析
趣味：日本史新書開拓、Web開発、ミステリ、数楽杯、TikZ(まいんさんに褒められました！！！)
おすすめのアニメ：よう実、ダークギャザリング、薬屋のひとりごと
得意なこと：無関係な事実同士をこじつけること
お問い合わせ：
$\mathbb{X}$→
@Nickname0628
LINEオプ→
「競技数学対策本部～やろうぜ！数楽( ´・∀・｀)～」
とまあこんなところでしょうか。なにかあったらいつでもDMどうぞ。
例のアレを見つけた経緯
ということで、ここからが本題です。すこーし冗長ですが我慢してください。
第1話 1/6公式を習う
僕は非進学校の文系だったので、数学Ⅱで1/6公式を習ったのは高2の終盤でした。ご存じかとは思いますが、1/6公式とは以下の公式です。
$$ \int^\beta_\alpha (x-\alpha)(x-\beta) \ dx=-\frac{1}{6}(\beta-\alpha)^3 $$
これ、問題を解いていると結構な頻度で使える便利な公式だとは思うんですが、なーんか物足りない感じしませんか？？そう、1乗$\times$1乗なんて汎用性に欠けるな、と思いましたよね？僕は思いました。そこで、$n$乗$\times$$m$乗まで拡張するのは流石に無理だと思ったので、$n$乗$\times$$n$乗で試してみよう、となったのが始まりです。
第2話 1/6公式の証明
教科書には(数Ⅲ範囲とされていた$\displaystyle\int(ax+b)^n \ dx=\frac{1}{a(n+1)}(ax+b)^{n+1}+C$は使えなかったので)ごちゃごちゃと書いてありましたが、僕は次のように示しました。かなり有名な証明ですが、自力で思いついたと錯覚したときの脳汁はすごかったですね。
\begin{eqnarray} \int^\beta_\alpha(x-\alpha)(x-\beta) \ dx &=& \int^\beta_\alpha(x-\alpha)\{(x-\alpha)+(\alpha-\beta)\} \ dx\\ &=&\int^\beta_\alpha(x-\alpha)^2+(x-\alpha)(\alpha-\beta) \ dx\\ &=&\left[\frac{1}{3}(x-\alpha)^3\right]^\beta_\alpha+(\alpha-\beta)\left[\frac{1}{2}(x-\alpha)^2\right]^\beta_\alpha\\ &=&\frac{1}{3}(\beta-\alpha)^3-(\beta-\alpha)\cdot\frac{1}{2}(\beta-\alpha)^2\\ &=&-\frac{1}{6}(\beta-\alpha)^3. \quad\Box \end{eqnarray}
第3話 $n$乗に拡張してみる
Twitterでこの等式を思いついた経緯を当てるクイズを出したところ、多くの人が$\displaystyle\int^1_0x^n(1-x)^n \ dx$から導いたのではないかと予想してくれましたが、残念ながら僕は工夫という言葉を知らないただのバk純情で素直なイイ子だったので、上の証明をそのまま$n$乗しました。つまり、
\begin{eqnarray} \int^\beta_\alpha(x-\alpha)^n(x-\beta)^n \ dx &=&\int^\beta_\alpha(x-\alpha)^n\{(x-\alpha)+(\alpha-\beta)\}^n \ dx\\ &=&\int^{\beta}_{\alpha}(x-\alpha)^n\Bigl\{(x-\alpha)^n+{}_n\mathrm{C}_1(x-\alpha)^{n-1}(\alpha-\beta)+\cdots+{}_n\mathrm{C}_{n-1}(x-\alpha)(\alpha-\beta)^{n-1}+(\alpha-\beta)^n\Bigr\}dx\\ &=&\int^{\beta}_{\alpha}(x-\alpha)^{2n}dx+{}_n\mathrm{C}_1(\alpha-\beta)\int^{\beta}_{\alpha}(x-\alpha)^{2n-1}dx+\cdots+{}_n\mathrm{C}_{n-1}(\alpha-\beta)^{n-1}\int^{\beta}_{\alpha}(x-\alpha)^{n+1}dx+(\alpha-\beta)^n\int^{\beta}_{\alpha}(x-\alpha)^ndx\\ &=&\Bigg[\frac{1}{2n+1}(x-\alpha)^{2n+1}\Bigg]^{\beta}_{\alpha}+{}_n\mathrm{C}_1(\alpha-\beta)\Bigg[\frac{1}{2n}(x-\alpha)^{2n}\Bigg]^{\beta}_{\alpha}+\cdots+{}_n\mathrm{C}_{n-1}(\alpha-\beta)^{n-1}\Bigg[\frac{1}{n+2}(x-\alpha)^{n+2}\Bigg]^{\beta}_{\alpha}+(\alpha-\beta)^n\Bigg[\frac{1}{n+1}(x-\alpha)^{n+1}\Bigg]^{\beta}_{\alpha}\\ &=&\frac{1}{2n+1}(\beta-\alpha)^{2n+1}+\frac{{}_n\mathrm{C}_1}{2n}(\beta-\alpha)^{2n}(\alpha-\beta)+\cdots+\frac{{}_n\mathrm{C}_{n-1}}{n+2}(\beta-\alpha)^{n+2}(\alpha-\beta)^{n-1}+\frac{1}{n+1}(\beta-\alpha)^{n+1}(\alpha-\beta)^n \end{eqnarray}
ここで、$n$の偶奇によって次のように場合分けされます。
(i) $n$が偶数のとき
\begin{eqnarray}
\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^ndx
&=&\frac{1}{2n+1}(\beta-\alpha)^{2n+1}+\frac{{}_n\mathrm{C}_1}{2n}(\beta-\alpha)^{2n}(\alpha-\beta)+\cdots+\frac{{}_n\mathrm{C}_{n-1}}{n+2}(\beta-\alpha)^{n+2}(\alpha-\beta)^{n-1}+\frac{1}{n+1}(\beta-\alpha)^{n+1}(\alpha-\beta)^n\\
&=&\frac{1}{2n+1}(\beta-\alpha)^{2n+1}-\frac{{}_n\mathrm{C}_1}{2n}(\beta-\alpha)^{2n+1}+\cdots-\frac{{}_n\mathrm{C}_{n-1}}{n+2}(\beta-\alpha)^{2n+1}+\frac{1}{n+1}(\beta-\alpha)^{2n+1}\\
&=&\Biggl(\frac{1}{2n+1}-\frac{{}_n\mathrm{C}_1}{2n}+\cdots-\frac{{}_n\mathrm{C}_{n-1}}{n+2}+\frac{1}{n+1}\Biggr)(\beta-\alpha)^{2n+1}
\end{eqnarray}
(ii) $n$が奇数のとき
\begin{eqnarray}
\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^ndx
&=&\frac{1}{2n+1}(\beta-\alpha)^{2n+1}+\frac{{}_n\mathrm{C}_1}{2n}(\beta-\alpha)^{2n}(\alpha-\beta)+\cdots+\frac{{}_n\mathrm{C}_{n-1}}{n+2}(\beta-\alpha)^{n+2}(\alpha-\beta)^{n-1}+\frac{1}{n+1}(\beta-\alpha)^{n+1}(\alpha-\beta)^n\\
&=&\frac{1}{2n+1}(\beta-\alpha)^{2n+1}-\frac{{}_n\mathrm{C}_1}{2n}(\beta-\alpha)^{2n+1}+\cdots+\frac{{}_n\mathrm{C}_{n-1}}{n+2}(\beta-\alpha)^{2n+1}-\frac{1}{n+1}(\beta-\alpha)^{2n+1}\\
&=&\Biggl(\frac{1}{2n+1}-\frac{{}_n\mathrm{C}_1}{2n}+\cdots+\frac{{}_n\mathrm{C}_{n-1}}{n+2}-\frac{1}{n+1}\Biggr)(\beta-\alpha)^{2n+1}
\end{eqnarray}
(i)，(ii)より
$$
\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^ndx=\sum^n_{k=0}\frac{(-1)^{n-k}{}_n\mathrm{C}_k}{n+k+1}(\beta-\alpha)^{2n+1}\tag{1}
$$
ここまで頑張ったところで、僕は困ってしまいました。確かになんかいいカンジになったけど！！シグマの計算だるい！！！！ということで、別のアプローチを考えることにしました。が、数Ⅱまでの範囲しかわからない僕にはなかなかいい方法は思いつきませんでした...
第4話 部分積分との出会い
そこで、恥を忍んで数学のN先生(僕とべるちゃその師匠とも呼ぶべきものすごいお方。数学オリンピック財団の人で、文系にもかかわらず僕がこんな風になってしまった黒幕。)に$\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^n \ dx$を簡単に表す方法はないか尋ねたところ、「漸化式チックに解けるね～」とニヤニヤと言われました。腹が立ちました。ただ、「積の微分公式を発展させる」というヒントを聞き出せたので頑張ってみることにしました。実は、これにとりかかる少し前に積の微分公式を自力で導けたことをドヤ顔で報告したので先生はそれを使えと言ってくださったのです。
$$ \{f(x)g(x)\}'=f'(x)g(x)+f(x)g'(x) $$
試しに、積の微分公式の両辺を積分してみました。ただし、$C$は積分定数。
\begin{eqnarray} \{f(x)g(x)\}'&=&f'(x)g(x)+f(x)g'(x)\\ \Longleftrightarrow\int\{f(x)g(x)\}' \ dx&=&\int \{f'(x)g(x)+f(x)g'(x)\} \ dx\\ \Longleftrightarrow \int f'(x)g(x) \ dx&=&f(x)g(x)-\int f(x)g'(x) \ dx+C. \quad\Box \end{eqnarray}
そう、皆さんご存じ部分積分です。上の証明は不定積分で書きましたが、当然定積分でも同様のことが成り立ちます。
$$ \int^\beta_\alpha f'(x)g(x) \ dx=\Bigl[f(x)g(x)\Bigr]^\beta_\alpha-\int^\beta_\alpha f(x)g'(x) \ dx $$
こうして、数Ⅲをやっていないのに部分積分は知っているという奇妙な人間が誕生したわけです。さて、部分積分を使って$\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^n \ dx$を考えていきます。
部分積分を与式に繰り返し適用することで、
\begin{eqnarray}
\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^n \ dx
&=&\int^{\beta}_{\alpha}\Biggl\{\frac{1}{n+1}(x-\alpha)^{n+1}\Biggr\}'(x-\beta)^n \ dx\\
&=&\left[\frac{1}{n+1}(x-\alpha)^{n+1}(x-\beta)^n\right]^\beta_\alpha-\int^\beta_\alpha\Biggl\{\frac{1}{n+1}(x-\alpha)^{n+1}\Biggr\}n(x-\beta)^{n-1} \ dx\\
&=&-\frac{n}{n+1}\int^\beta_\alpha(x-\alpha)^{n+1}(x-\beta)^{n-1} \ dx\\
&=&\frac{n}{n+1}\cdot\frac{n-1}{n+2}\int^\beta_\alpha(x-\alpha)^{n+2}(x-\beta)^{n-2} \ dx\\
&=&-\frac{n}{n+1}\cdot\frac{n-1}{n+2}\cdot\frac{n-2}{n+3}\int^\beta_\alpha(x-\alpha)^{n+3}(x-\beta)^{n-3} \ dx\\
&\vdots&\\
&=&(-1)^n\frac{n!}{\frac{(2n)!}{n!}}\int^\beta_\alpha(x-\alpha)^{2n}(x-\beta)^0 \ dx\\
&=&(-1)^n\frac{(n!)^2}{(2n+1)!}(\beta-\alpha)^{2n+1}\tag{2}
\end{eqnarray}
後から知りましたが、これはベータ関数(第一種オイラー積分)をガンマ関数(第二種オイラー積分)を用いて表示したものでした。
$(2)$で示した等式よりももっと一般に、非負整数$m,n$において次の等式が知られている。※区間の変換等は割愛します。
$$
\int^\beta_\alpha (x-\alpha)^m(x-\beta)^n \ dx=(\beta-\alpha)^{m+n+1}(-1)^n\int^1_0 t^m(1-t)^n \ dt
$$
ここで、ガンマ関数の表示を用いると、
$$
\int^1_0 t^m(1-t)^n \ dt=B(m+1,n+1)=\frac{\Gamma(m+1)\Gamma(n+1)}{\Gamma(m+1+n+1)}=\frac{m!n!}{(m+n+1)!}
$$
ゆえに、
$$
\int^\beta_\alpha(x-\alpha)^m(\beta-x)^n \ dx=\frac{m!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}
$$
いよいよ物語はクライマックスに突入します。
最終話 運命の赤いイコール
さて、$\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^n(x-\beta)^n \ dx$をいいカンジに表すという当初の目的は達成されたわけですが、ここであることに気づきました。$(1)$と$(2)$イコールでつなげられるやん、と。そしてつなげてみた結果得られたのが"アレ"だったわけです。
$(1),(2)$より、
$$
\sum^n_{k=0}\frac{(-1)^{n-k}{}_n\mathrm{C}_k}{n+k+1}(\beta-\alpha)^{2n+1}\textcolor{red}{=}(-1)^n\frac{(n!)^2}{(2n+1)!}(\beta-\alpha)^{2n+1}
$$
すなわち、
$$
\Large
\boxed{(2n+1)!\sum^n_{k=0}\frac{(-1)^k{}_n\mathrm{C}_k}{n+k+1}\textcolor{red}{=}(n!)^2}
$$
このようにして僕のヘッダーは誕生したわけです。
まあ、最初はこんなに綺麗じゃなかったんですけどね.....
https://x.com/Nickname0628/status/1767535594140500028
https://x.com/Nickname0628/status/1768975738286526777
](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FaZXghZQBVrOgexzTf4gg.png?alt=media)
あの日の悲しみ(シグマの上端で嘘ついてる)
](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FjkaBChzfVpdDMvkkD6fA.png?alt=media)
あの日の苦しみ(-1の指数嘘ついてる)
過去ツイ見てたらあまりにイタくて虚しくなった。なお、N先生が教えてくださったのですがこの等式は高階差分を用いて示すこともできるそうです。
組み合わせ的な解釈の考察
さて、この等式について僕のオプ(上述)で話していた時、「やっぱ組み合わせ的に解釈してみたいよね～」みたいな話になりました。あの頃は全然思いつきませんでしたが、今になって少し考えたことを書いてみます。
ただし、ここから先には論理的な誤りが含まれる可能性が多分にありますのでご注意ください。
赤玉が$n$個, 青玉が$n$個、黄玉が$1$個で計$2n+1$個の玉がある. これらの玉を一列に並べるとき, すべての赤玉が黄玉の左側にあり, かつすべての青玉が黄玉の右側にある確率を求めよ.
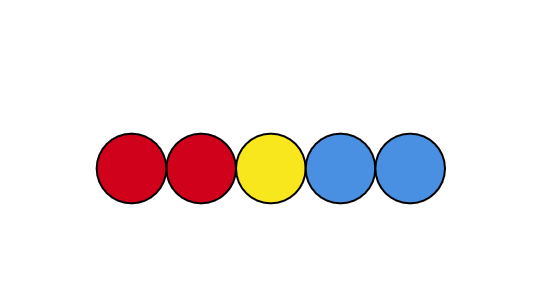n=2の時の例
この問題について考えてみます。$2n+1$個の玉の並べ方は全部で$\displaystyle\frac{(2n+1)!}{n!n!1!}$(通り)です。一方、すべての赤玉が黄玉の左側にあり, かつすべての青玉が黄玉の右側にあるような並べ方は明らかに1通りしかありません。よって、求める確率は$\displaystyle\frac{1}{\frac{(2n+1)!}{n!n!}}=\frac{n!n!}{(2n+1)!}$です。
少し別の見方をしてみましょう。(ここからがアヤシイところ)
$n$個の青玉がすべて黄玉の右側にある事象を$B$、赤玉$i \ (i=1,2,\dots n)$が黄玉より右側にある事象を$A_i$とします。
すると、求める確率は$P(B\cap\overline{A_1}\cap\overline{A_2}\cap \cdots \cap\overline{A_n})$となりますね？(青玉が黄玉の右にすべてあり、かつ黄玉の右に赤玉が1つも並ばない確率。)
一方これは、包除原理を用いることで、$\displaystyle\sum_{k=0}^n (-1)^k\sum_{\substack{I \subset \{1,2,\dots,n\} \\ |I| = k}}P\bigl(B \cap \bigcap_{i \in I} A_i \bigr)$(ただし、$k=0$のときは空集合なので$P(B)$)と表すことができます。これが実は、$\displaystyle\sum^n_{k=0}\frac{(-1)^k{}_n\mathrm{C}_k}{n+k+1}$に等しいのではないか、というのが僕の主張です。今のままだとチンプンカンプンだと思うので、少し実験しましょう。
$n=2$の場合で実験
求める確率は$P(B\cap\overline{A_1}\cap\overline{A_2})$です。包除原理より、これは$\displaystyle\sum_{k=0}^2 (-1)^k\sum_{\substack{I \subset \{1,2\} \\ |I| = k}}P\bigl(B \cap \bigcap_{i \in I} A_i \bigr)$すなわち$P(B)-\{P(B\cap A_1)+P(B\cap A_2)\}+P(B\cap A_1\cap A_2)$に等しいことがわかります。これらを順にみていきましょう。
(i)$k=0$のとき
$P(B)$の値を求めます。黄玉が1個、青玉が2個あるとき(赤玉は1個も選ばない)に黄玉が一番左に来る確率なので、
$$
P(B)={}_2\mathrm{C}_0\cdot\frac{1}{\underbrace{2}_{\text{青玉の個数}}+\underbrace{0}_{\text{赤玉の個数}}+\underbrace{1}_{\text{黄玉の個数}}}=\frac{1}{3}.
$$
(ii)$k=1$のとき
$P(B\cap A_1)+P(B\cap A_2)$の値を求めます。黄玉1個、青玉2個に加え赤玉2個の中から1個を選んだ計4個を並べる際に、黄玉が一番左に来る確率なので、
$$
P(B\cap A_1)+P(B\cap A_2)={}_2\mathrm{C}_1\cdot\frac{1}{2+1+1}=\frac{1}{2}.
$$
(iii)$k=2$のとき
$P(B\cap A_1\cap A_2)$の値を求めます。黄玉2個、青玉2個、赤玉2個の計5個の玉を並べる際に、黄玉が一番左に来る確率なので、
$$
P(B\cap A_1\cap A_2)={}_2\mathrm{C}_2\cdot\frac{1}{2+2+1}=\frac{1}{5}.
$$
(i),(ii),(iii)より、求める確率は
$$
P(B\cap\overline{A_1}\cap\overline{A_2})=\sum^2_{k=0}\frac{(-1)^k{}_2\mathrm{C}_k}{2+k+1}=\frac{1}{3}-\frac{1}{2}+\frac{1}{5}=\boxed{\frac{1}{30}}.
$$
他方、$\d\frac{2!2!}{(2\cdot2+1)!}=\frac{1}{30}$であり、なんか一致していそうです。
$n \geq 3$でも同様に帰納的に考えることで、包除原理を用いた確率の求め方が$\d\sum^n_{k=0}\frac{(-1)^k\C{n}{k}}{n+k+1}$となり、直接数えた確率の求め方が$\d\frac{(n!)^2}{(2n+1)!}$となるため、両者は等しいことから等式が組み合わせ的に解釈できるはずです。多分。
これはこの前べるちゃそと食べたラーメン。関係はない。
おわりに
いかがだったでしょうか？下手な文章をだらだらとすみませんでした。他の方の記事に比べて随分とレベルが低いものになりましたが、ご容赦ください。今思い返しても、上の組み合わせ的解釈はどこかしらで嘘をついているような気がするのでもっと良い解釈があったら教えていただきたいです。(記事に掲載させていただきます。)
最後になりますが、等式の発見経緯をTwitter上で考察してくださった方々、色々と教えてくれたN先生、一方を$n$から$m$に変えたときの考察を手伝ってくれたべるちゃそ、そしてなにより、ヘッダーを描いてくださったことでのらりくらりと記事を書く書く詐欺を続ける道を断って記事を書くいいきっかけを作ってくださった地理奈(
@Tiri7_Ma1tha_
)さん、ありがとうございました。
怠惰な僕が次の記事を書くとは思えませんが、もし書くとしたら$\mathrm{\LaTeX}$や$\mathrm{Ti}k\mathrm{Z}$関連の記事か、数楽杯に関する記事だと思われます。それではまた。
