コラッツ予想の数列の一般項について

ボトムアップ方式で、すなわち、すべての正の整数が最終的にコラッツ計算を施すと1になることを証明する代わりに、1がすべての正の整数に逆計算でつながることを証明したいと思います。

その図において、偶数だけ、奇数だけをそれぞれ考えると、その並びに規則性があることに気づきました。

そこで、コラッツ計算とは逆に、s,tがすべての正の整数をとるとき、偶数を一つの式、奇数を二つの式で表すことを考えました。
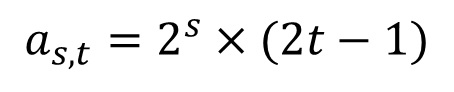偶数式
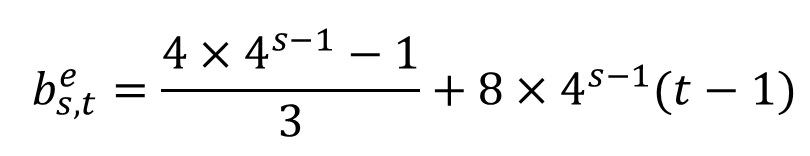奇数式e
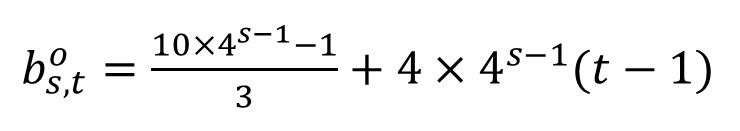奇数式o

次に、縦にs、横にtをとって、一般項の値を計算して表にすると、それぞれ次のような値になります。
（奇数は、3倍して1を足したときに、奇数になるまで2で割る回数が偶数回か奇数回かで、式が異なります。グレーの行とホワイトの行と交互に示します）
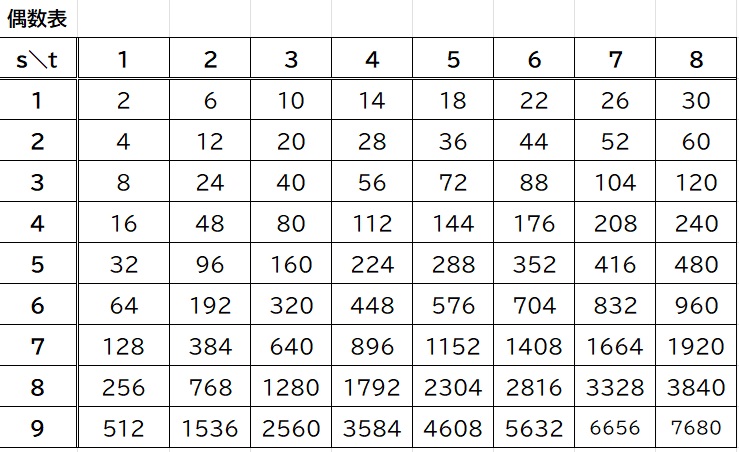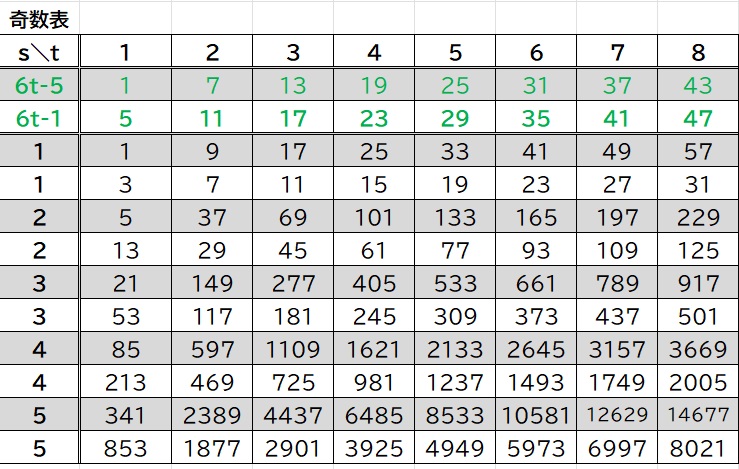偶数表
奇数表

この表の値は、調べてみると、すべての偶数、奇数が表せそうですし、重複がありません。
そして、偶数表にも、奇数表にも、縦にコラッツ計算があらわれています。（奇数は、縦の、グレーのみ、ホワイトのみを見ると、奇数の枝がそれぞれあらわれています。グリーンの数が、その列の枝が連結される数です）
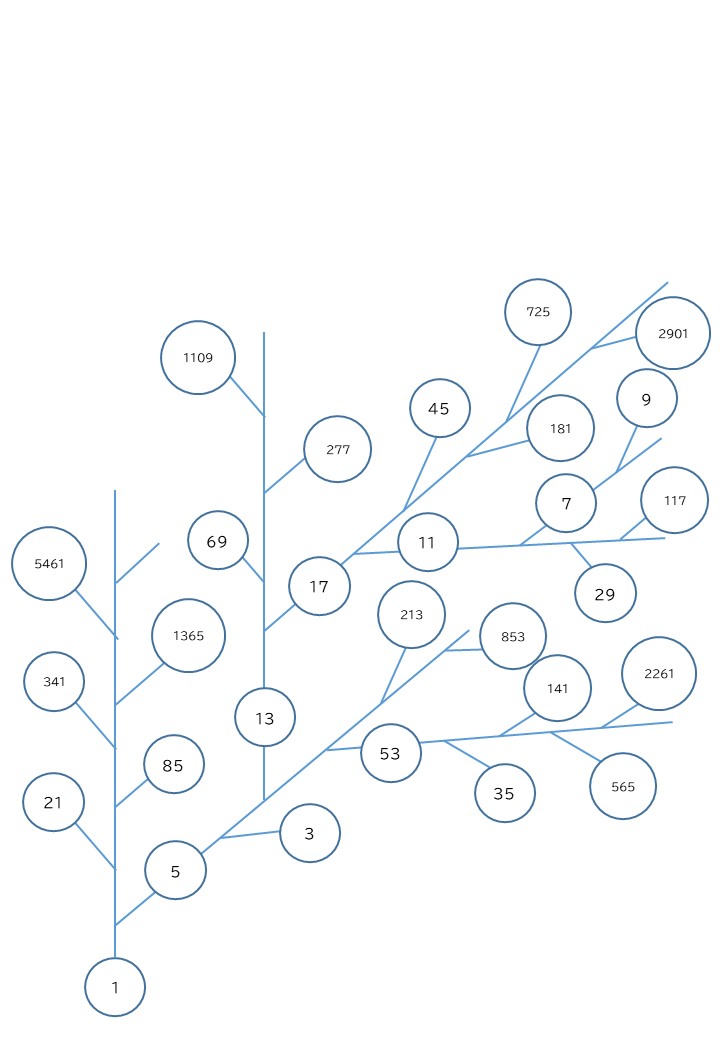奇数のみのコラッツツリー

1を起点として、すべての正の偶数、奇数が、これらの3つの一般項で示される数列によって並ぶので、コラッツ計算により、すべての正の整数は1に到達すると言えると思いました。
（これらは別の媒体でも文章化し、まとめています。数学的帰納法による証明にもチャレンジしています https://sugakunoheya.blog.fc2.com/blog-entry-24.html）