数理整備まとめ　極限定義と同相性　無限遠点、次元概念、計算モデル拡張　循環基本原理・量子無原速原理　解析接続写像による構造的均衡

数理整備及び循環基本世界に関する研究

はじめに

a+a=2a
a-a=0
a×a=$a^{2}$
a/a=1

a+a=2aは左と右の対称性が破れているのは明らかである(a個ずつ2名で持つのと2a個1名で持つなど)
2a=2aとしても時間対称性が破れているかもしれない、空間対称性が破れているかもしれない、少なくとも表記上の位置の対称性は破れている
つまり、a+aが2aと全グレードレベルで同じなのではない、両者を同じとして扱うから同じなのである
数の抽出、数対称性を扱う、四則算をイコールとして扱う、それが数理である
本稿は、異対称性間における数対称性(同相性)に関する数理整備、それに伴う概念拡張、そこから導き出される循環基本世界に関する研究である

論点1　極限の厳密定義による同相性の数理整備　～数理の不都合性の解消と不都合性のない概念の拡張、異対称性間通信～

1.極限の検証

無限概念のもとでは、素数実数が無限にある(時間次元永続無限)一方で素数砂漠も無限にある(時間次元永続超越無限、空間次元無限)
0=1/∞(あるいは実数/∞など)、1/0に代入可能とすると1/0=1/(1/∞)、さらに式変形可能とすると∞(計算不可)となり、素数砂漠無限となる世界などの前提がなければ1/0計算不可とする現代数理上扱えない
極限厳密定義を検証し、時間次元無限概念・空間次元無限概念を整備する

(1)極限・無理数の有間性

現行イプシロン・デルタ(ε-δ)論法による0.(9)=1となる極限定義の実態は、Σ算を無条件で使えるとするかのような、円周率3.1415…が割り切れない有間解であることとの整合性を欠く計算不可世界～念自在世界(何でもありの世界)の結論なのである
$$ \sum_{n=1}^{∞}9(1/10)^{n} = 1　ただし、計算不可世界の結論 $$
こちらのΣ算が1(計算不可世界)、近づき終わり限りがある極限違反が念自在世界の結論なのであってその場合は円周率も無間解(公理は、「ある数学体系を作るための、最も基本的な前提条件」の意、Σ算による$1/10^{n}$=$1/10^{∞}$の超越的代数操作はn=∞の代入を直ちに可能とし、∞グレード拡張を可能とする、本稿では、この超越的代数操作を代数の公理とする)となる、0.(9)<1(計算可世界)が厳密解である、無限算の条件については(3)にて後述する

例として観測者実験を挙げる
小数点以下第一位から無限まで順に観測する観測者を置く
①0.9の時は1と0.9の差は0.1、②0.99の時は1と0.99の差は0.01、②の時x軸(とする)のグラフの大きさを10倍に拡大したものを観測者に届ける
このように桁が変わる毎にグラフサイズを10倍に拡大したものを観測すると常に最初の0.1分の間隔が無限に確認できる…③
イプシロンエヌデルタ論法が厳密に正しいとしても、その解は計算不可世界～念自在世界の結論であり、無限に0に届かない③が同時に存在する(無理数有間解、$1^{∞}$=1)

時間永続無限においては、どの時間帯においても0には届かないのである
例として、キーボードの「9」キーを押し続けると、0.999…という終わらないシーケンスが生成されるプロセスを挙げる
この動作は、1に到達することのない無限の時間永続性を示すものであり、円周率が割り切れない無理数解無し(有理数解を持たない代数的解無しの意味である)の超越数有間解であることと同様の意味である
∞個の地点に行けば間隔はないが、実数世界ではない

結論として、極限は絶対収束すると限りがあったことを意味し、1に到達すると9が無限に続かなく限りなく近づくという概念に違反する
任意の小さなイプシロン(ε)に対して、必ず対応するより小さなデルタ(δ)が出現することは、限りないという概念に整合する、しかし、それは近づき終わることを意味するわけではなく、論理飛躍である
0.(9)+1/$10^{n}$= 1　(9の並びをn個とする)
1/$10^{n}$は限りなく小さくなることができるが、nの値がどんなに大きくなっても1/$10^{n}$が0になることはない、0になるのは1/∞(計算不可世界)のような場合であり、実数の数の大きさとは別の議論である、計算可世界では回数無限(∞ 個)も現出できない
イプシロン・エヌ(ε-N)論法及びイプシロン・デルタ(ε-δ)論法は素数砂漠が無限に続く結論である時間永続超越無限であって、素数が無限に続く結論である時間永続無限ではないのである
円周率　素数　時間次元無限(時間永続－有限個数)
ε-N論法　ε-δ論法　素数砂漠　空間次元無限　時間次元無限(時間永続超越－無限個数現出)

Lim同様、0.(9)は小数点以下9が無限に続くという概念であり、$\pi$=円周/直径>3.1415…割り切れない無理数有間解(用語の確認として、無理数は分数で表せない実数、$\sqrt{2}$は$x^{2}$-2=0の解であり代数的無理数、整数係数の方程式の解なしが超越数である)、1/7>0.(1)4285(7)割り切れない有間解(0.(1)4285(7)は無理数と考えられる　循環数だから無限個無間解になる、超越数は循環数ではないから無限個有間解になるのではない、永続無限の意味の無限個(どの時点においても有限個であり、無限個それ自体は現出しない)有間解が正しい、有間永続であるから実数永続するのである、ダブルスタンダードである両者の整合が必要であるが、表記通りと思われる実数永続が相当)、0.(1)～0.(8)無理数(9×0.(1)+1/$10^{n}$=1　1の並びをn個とする)、n＜1の時、$\lim_{n\to1}$ n=0.(9)無理数有間解<1、n→=1であれば近づき終わる意味n=1である

実数(Real Numbers):$\mathbb{R}$
有理数(Rational Numbers):$\mathbb{Q}$
無理数(Irrational Numbers):($\mathbb{R}\setminus\mathbb{Q}$)
差集合 (Set Minus; Set Difference):$\setminus$
和集合(Union):$\cup$
論理積(Logical Conjunction):$\land$
集合の要素(Element Of):$\in$
集合の要素ではない(Not An Element Of):$\notin$
同相である(Homeomorphic To):$\cong$
同相ではない(Not Homeomorphic To):$\not\cong$
($\mathbb{Q}$$\cup$($\mathbb{R}\setminus\mathbb{Q}$)=$\mathbb{R}$)$\land$(∞$\notin$$\mathbb{R}$)
ε-N論法の収束論理によると、無限級数、$$ \lim_{N \to \infty} \sum_{n=1}^{N}1/10^{n}=1/9(無間確定、計算不可世界の結論) $$は実数ではない
実数$x\in\mathbb{R}$とすると、$x^{2}\geq$0より、$i^{2}$=－1($i^{2}$ result)$\notin\mathbb{R}$ (複素平面上の虚数計算－1$\not\cong$実数平面上の－1、よって、疑似実数－1($i^{2}$ result)＝－1$\land$－1($i^{2}$ result)＝$i^{2}\notin\mathbb{R}$)
疑似実数(Pseudo-Real Numbers($\mathbb{P}$)): 本稿では、Σ算による∞級数収束値や$i^{2}$の計算結果は$\mathbb{P}$の集合に属すると定義する、－1($i^{2}$ result)は概念拡張済みであり、$i^{2}$に変換可能であるが、実数の－1は概念拡張なしでは、$i^{2}$に変換できない
7/9 + 1/9(無間確定) + －1($i^{2}$ result) = －1/9 (無間確定 and $i^{2}$ result)
これは、量子情報におけるコヒーレンスとエンタングルメントの追跡に類似する(∞操作による疑似実数$\mathbb{P}$の確定)
無限概念拡張済 (Infinite (∞) Conceptually Extended): ∞ce
虚数概念拡張済 (Imaginary ($i$) Conceptually Extended): $i$ce
7/9 + 1/9 (∞ce) + －1 ($i$ce ) = －1/9 (∞ce$\land$$i$ce)

素数が無限にあるという内容は、∞個ある素数を個々の具体的な素数として表す場合素数永続となる、つまり、∞個の現出と実数永続の動的概念を明確に区別する必要があり、式や数(3.1415…など)の更新プロセスとして表現可能である
自然数 (Natural Numbers):$\mathbb{N}$
有限小数 (Terminating Decimals):$\mathbb{T}$
全ての、任意の (Universal Quantifier):$\forall$
存在する (Existential Quantifier):$\exists$
n: 桁数あるいは項の総数
$n$ $\in$ $\mathbb{R}$ $\geq$ 0 とすると、本稿では有理数に該当しないとする∞個無間解の循環小数(0.(9)など)や計算永続する無理数が含まれるので、ここでは範囲を以下に限定する
($n$ ∈ $\mathbb{N}$ $\cup$ $\mathbb{T}$) $\land$ $\forall n$$\exists n'$ (0 < $n$ < $n'$)

1/∞=0、1/0(計算不可)より、無間グレードの無限は、実数の公理a/a=1(本稿上実数の公理として扱う)、1/0(計算不可)の数理においては、式に条件を加えない条件下では、∞(計算禁止)となり扱えない(不都合性の無い式代入・式変形)
1/0は拡張しないと計算不可、同様に無間グレード無限は拡張しないと計算不可となる
計算可能なのは、実数が永遠に続くという意味の無限であり、超越的な実数は無理数で代数的解無し、どの地点を切り取っても${}\mathrm{ V }_p$×0=0、0/${}\mathrm{ V }_p$=0であり、それは実数であり0.(9)<1となる無限なのである
${}\mathrm{ V }_p$(Value Persistent): The value at a certain point in time-persistent infinity where the real numbers continue forever (perpetually continue); 実数永続無限のある時点の値
なお、実数永続無限は実数無限(大きさ無限を加えたものを拡張実数無限、複素数を加えたものを複素実数無限とする)とも呼ぶこととする

表記した部分それ以降という書き方も可能である
例
0.(9)＝0.a(9)　a=小数点以下、Σ(10000↑↑↑10000)桁9が並ぶ　以降(9)という表記など
9の並びをn個(n:項の総数)とすると数理上、
0.(9) + 1/$10^{n}$ = 1
$$ \sum_{k=1}^{n}9(1/10)^{n} + 1/10^{n} = 1 $$
そもそも、1/3=0.3あまり0.1、0.33あまり0.01であり、数理上のイコール(等価)を厳密に満たす必要があるのは言うまでもない
実数無限及び無間無限両者に対応の表記としてはこちらのΣ式が正しく、Σの場合、拡張概念である無時間にて無限回足し合わせた概念通りのΣ表記がより正しい
Σのイコール変換については、(2)にて後述する

0.(9)の実数無限は、1/$10^{n}$分の隙間があり(有間)、円周率同様実数が無限に続くのであって無間ではない、どこを切り取っても実数という意味の無限であって、無間無限は別グレードの無限であるのは明らかである

一方では円周率、3乗根など実数永続無限で割り切れずに計算永続、一方では0.(9)、ε-δ論法、Σ収束など無間無限で収束し計算完了という無限概念に対する混乱が見受けられるのである

以上より、用語を次のように見直す
極限は、ある値に限りなく近づく意味とする
∞は、素数確率0(1/∞=0(∞ce))と定義する(素数無限世界には無条件では持ち込めない)、無間解を持つ意味である
超越実数(超越数)は、実数が永遠に続く無理数で(新分類では無間解時に)代数的解無しの意味とする、円周率3.1415...が割り切れない超越数有間解無理数解無しであることから、0.999…、0.(9)などの表記は実数永続とするのが相当(実際永続循環するという内容であり、計算完了しない動的概念とするのが相当)、実数永続においては時点有限個であり、∞個という数は現出しないことに留意、実数が無限に続く概念と無限個という数が現出する概念は別物、∞個だと円周率も端数0の無間解となるのであり別表記とすべきであり、Σ式で表記可能である、素数砂漠が無限に続く結論は素数無限世界には持ち込めない、実数表記可能な素数が永続増加するのである、1/0計算不可の計算可能世界では、時点解が得られる意味である
実数が永遠に続く無限を実数永続無限(実数無限、大きさ無限を加えたものを拡張実数無限、複素数を加えたものを複素実数無限とする)とする、永続数から概念飛躍ないし永続数超越した場合は次の大きさ無限
大きさ無限(無間無限)は、無間解を持つ意味とする、∞などの表記
lim(n→超越実数グレードb)は、無理数解を持つ(ただし、グレード最下位の超越実数に限りなく近づく場合は超越手前想定)
lim(n→無間無限グレードb)は、無間解を持つ(ただし、グレード最下位の無間無限に限りなく近づく場合は、無間に到達手前最大グレードの超越実数想定)
n→無間無限グレードb、n→超越実数グレードbと表記があれば少なくともグレード最下位超の無間無限、超越実数になる意味とする(グレード最下位=グレードa<グレードb)、なお、無間無限は、大きさ、個数、速度など様々な種類がある
上記${}\mathrm{ V }_p$×0=0、0/${}\mathrm{ V }_p$=0、$\lim_{n \to 1}$　(n＜1)　n=0.(9)<1　である
lim(n→=)は、近づき終わる意味である(実質的代入)
$\lim_{n \to 1}$n=0.(9)<1(n<1、$\pi$の数値展開は割り切れない)、$\lim_{n \to =0}$1/n=∞(1/0 grade)、$\pi$=円周/直径、1/7は計算完了(静的)、3.1415…、0.(1)4285(7)は計算永続(動的)、時間概念拡張(永続概念拡張)である

(2)大きさ無限の無間性

絶対収束の時は
$$ \sum_{n=1}^{∞} 9(1/10)^{n}=9(1/10+1/100+ … +1/10^{∞}) $$
9×((1/10)/(1-1/10))=9×(1/9)=1
ここで、$9/10^{∞}$=0であれば
9+0.9+0.09+0.009+…+$9/10^{∞-1}$　　　　 =10x
　 0.9+0.09+0.009+…+$9/10^{∞-1}$+$9/10^{∞}$=x
9-$9/10^{∞}$=9x　x=1という理屈となるが(9/10)/(9/10)という実数変換式は厳密なレベルで合っているといえるだろうか、9/実数>0、実数以外の計算不可世界の概念数$9/10^{∞}$=0より、Σ以外の式に変換した途端計算禁止となるのである(計算不可世界の結論であって、計算可世界と同相ではない)

ここで素数確率より考える
任意の大数xについての素数確率の近似値1/$\log_{x}$は値が大きくなる程、素数がある確率は限りなく小さくなる
故に、任意の大数においては、本議論において、
素数確率=1/任意の大きい値　と考えて差し支えないものとみなす
ここには素数は無限にあるので確率が0になることはない
ただし、素数が連続で出てこない素数砂漠という概念が無限に続く、つまり
素数確率=1/任意の大きい値=0　となる概念も同時に存在する(こちらは計算不可世界)

素数の解としては、素数砂漠が無限に続く計算不可世界の結論を持ち込めなく、実数が永続する意味においては素数実数永続無限が正しい
ε-N論法、ε-δ論法のみ(計算不可世界～念自在世界の結論であり、その世界でしか通用しない)をもって極限厳密定義とする理論数学上では、計算可世界の結論、計算不可世界の結論、念自在世界の結論が未整備なのである。この点は(4)にて後述する。

上記が何を意味するのかどの階層の話なのか、例として、以下のやり取りを想定
Q.(Question)素数って無限にあるよね？　A.(Answer)素数砂漠は無限にあります
Q.無限にある素数のどこを選んでもそれは100%素数実数ですね？　A.無間無限のどこを選んでも素数砂漠です
Q.想定では素数実数は無限にあるのですが、素数はどうなったのですか？　A.承知しておりますが、本世界のキャパオーバーとなる素数は無間無限世界の結論として処理していますので、本世界ではそのような手法による素数実数の無限性は検証断定できませんでした
計算可世界の問いに対して計算不可世界の回答である。このように、日常生活においても一方は社会レベルの階層の話、一方は個人レベルの階層の話をしていて会話にならない場合など起こりうる内容である

数式及びその結論は当該数理に当てはめる必要がある
Σは、同時に足し合わせるのであり空間有限永続無限(空間が有限あるいは永続無限であり、時間、速度、回数、数値などの無間無限を同時計算と解釈)であるが、Σ算でなければ、つまり、拡張概念がなければ、大きさ無限で計算不可か永続無限で計算可かの二通りの表記であり、計算可能が前提であれば永続無限となる
両者を∞表記する場合は、実数∞(実数永続∞)、無間∞などと区別して表記するとわかりやすい

(3)ゼロ無限算と回転集積体(瀬織津)

$1/A^{(a\infty+b)} \iff 1 = 0 × A^{(a\infty+b)}$
実数公理a/a=1より、
$A^{(a\infty+b)} × (A^{(a\infty+b)})^{-1} = 1$　ただし、COR参照(計算順序記録 Calculation Order Record (COR) データ添付などが必要である、CORは取りうる計算可能範囲などを付記したものや、$e$導出のように明確な手順が好ましい)…①
すなわち、0(1/無間無限)とは無限概念拡張(∞ce)であり、本来、無限概念拡張済みであればゼロ除算は可能であり、未拡張であればゼロ自体扱えない
底・指数項が同一であれば鏡像対称性より $1$ となる

ここまで確認の意味で再度まとめると、実数無限は実数が永遠に続くという意味の無限であり限りはない、大きさ無限は無間解を持つ無限であり1/∞=0、ここで、1/0(計算不可)の数理においては、式に条件を加えない条件下では、∞(計算不可)となり扱えない(不都合性の無い式代入・式変形)
これを実数公理a/a=1 及び 1/0(計算不可)世界における数理上扱うには概念拡張条件を式に加える必要があり、Σやただし条件がその例である

ゼロ無限算の例として、球円モデル無限速度による循環系である回転振動体を挙げる
通常の微積は、rを半径とすると、球体積のr微分が球の表面積、円面積のr微分が円周であるが、本稿では新たに球円微積概念を用意する(なお、本稿は概念考察であり数式モデルの構築は共同研究などとしたい)、ここでは議論簡略化のため、完全球、完全円、完全点のみを考慮対象とし、全グレード形態を点(みえない球 Invisible sphere (IS)、みえない円 Invisible Circle (IC)などエーテル上のみえない形)にしたあとの無限微分は(4)、バリエーションの詳細は論点2-2にて後述する
・球面上においては、円環を無限に集めたものが球面積である
・円環上においては、中心点からの半径rの点を無限に集めたものが円環である
ここで、以下変換グレード 0 とする。
球面積 = 4$\pi$$r^{2}$
円環 = 2$\pi$$r$
中心点 = 0
ここでいう微積とは、あるものとその回転体全集合(回転集積体)の意味である、点回転体$0^{∞}$(∞ = 無間無限、より正確には回転体を示す積分表示が必要、無間グレードによってゼロ対称性を破る回数・値などが変化する、r上に実数無限や低グレード大きさ無限の値なども)によって、位相転移が行われ、その回転体が円、円の回転体が球面である、次に、4$\pi$$r^{2}$は、無限遠点からみると中心点 0 点となり、球面回転体の無限回転によって顕れる回転体が円グレード2回転体である(以下略)、中心点 0 点からの微分は、変換グレード-1(みえない球(IS) → みえない円(IC))である(以下略)、なお、球円微積においては、円面積は円集合、球体積は球面集合として算定する
・円回転体は、その場回転(円・球)、トーラス回転、網の目(円縦横)回転
・球回転体は、その場回転(球)、数珠回転(無限速トーラス)
ここまで、一方向循環回転体の場合であり、点スピン、円スピン、球スピンの方向がそれぞれ異なり、点スピンかつ円スピンなどが想定される、本稿では、循環回転体を閉連続体と呼び、循環系毎に1次元構築と捉える、直線や螺旋は開連続体と呼び、無限遠点でゼロ点となるのであり、その時点で1次元構築と捉える

時間微積において、積分を回転集積体と考えると
速度の積分が時間分の距離、距離の積分は距離分の空間、空間の積分は空間分の集積体(イデア結晶情報体想定)、情報体の積分はオーン世界(ॐ=オーン)、オーン世界の積分は全世界、全世界の積分は全存在、全存在の積分は全創造、全創造の積分は全神聖を想定

(4)回転集積体分靈(須勢理)と同相(数対称性)

上記(3)において、0点から円への積分による位相のずれは想定したが、みえない球(0点)からみえない円、みえない円からみえない点 Invisible Point (IP)への微分などにおいても位相のずれはないか要検証、球や開連続体を点になるまで無限遠点視点移動した際の視点位置や点からみえない球への視点変換、ゼロ無限算による対称性の破れによる位相のずれが想定されるのである
以降、みえないみえない球(IS 2)、みえないみえない円(IC 2)、みえないみえない点(IP 2) → みえないみえないみえない球(IS 3)、以下略(全グレード)
加速度a=$mc^{2}$(m=速度,c=角速度)
微分の正体 －無限次元行列－【ずんだもん解説】
https://youtu.be/OZDM1VA-rU0

ここでファンタジーを考える、制限世界では必要な想定である
東の森のもにょ
幻獣もにょ　もにょもにょしている、もふもふとはちょっと違うゆるふわキャラ、実数の無限性を約束しつつその世界の許容量を超える巨大数を無間グレードへと飛ばす、宇宙開闢に匹敵する56億7千万テラアーデルハイドの光エネルギーが有名である、見かけで討伐に行くと並の神々クラスでは瞬殺される、無限光アインソフアウルは対処しきれない、もにゅもにゅになってもにゅ～(バタンキュー)と叫ぶらしい(アウル談)、天神アウルのペット的な僕(しもべ)

念自在世界の代表例がイプシロンエヌデルタ論法(東の森のもにょ、ファンタジーと何らかわらない、もにょ論法)である
極限は限りなく近づくで定義が終わっている
限りないのであるから、ある数を上回るエヌ・デルタが出てくる所までは妥当であるが、それが1/0計算不可の数理において近づき終わることを意味するわけではない、超越数有間解(無理数解無し)である
(1)にみるように、最下位グレード以外の大きさ無限に限りなく近づくことによってその下位グレードの大きさ無限になることが想定されるのであり、エヌ論法は計算不可世界においては成立する、ただし、計算不可世界の結論は1/0計算不可の数理には持ち込めない(同相ではない)
デルタ論法は、円周率が実数解に限りなく近づいても割り切れない超越数であり、実数が永続する意味において無間解にはならないことにも、限りなく近づくという極限概念にも違反する、また実数が永続するという意味でないのならば大きさ無限、計算不可となるのである
念自在だから0=1=2=3=0.(9)でしたと言うのと式に条件を表示しない意味において同値である
以上より
デルタ論法　念自在世界の結論　なんでもあり(なしも可)
エヌ論法　1/0計算不可世界(計算不可側)の結論　無間解
但し、最下位グレードの大きさ無限に限りなく近づき近づき終わる場合、同グレードの大きさ無限になる場合は念自在世界の結論
実数永続　1/0計算不可世界(計算可側)の結論　有間解(循環永続・非循環永続、無理数解なし)

(3)でみた時間次元、空間次元などにつき再掲する、ここでの無限は無間無限である
・速度次元$\in$時間次元(加速永続と無時間永続の同時存在、回数無限)
・時間次元$\in$空間次元(素数永続と素数砂漠永続の同時存在(時空パラレル)、空間無限)
・空間次元$\in$情報次元(量子重ね合わせ、時空プログラムのイデア結晶、確率論・アカシックレコード、情報無限)
・情報次元$\in$オーン(ॐ)世界次元(ॐ世界無限)
・オーン(ॐ)世界次元$\in$一なる次元(全共鳴無限)
・一なる次元$\in$存在次元(存在無限)
・存在次元$\in$創造次元(創造無限)
・創造次元$\in$神聖次元(神聖無限)
 
速度∞は上記全てに対称性を持つ、体積(3次元情報)を線(1次元情報)において処理できる意味である(速度対称性)
無限速に達したあと、加速度0から加速度∞想定、加速度0は加速世界からは停止世界である
実在認識世界に当てはめると視覚静止世界(物が止まってみえる)が挙げられる
速度次元以下の例として、加速度、加加速度、加加加速度、$d^{n}x/dt^{n}$(n$\in\mathbb{N}$ or ∞ パターン、位置(x)の時間微分)、加えて、微分積分全グレード(ゼロ無限算を含む)などを想定

対称性論議において対称性の破れが0であれば、同相とみなせるかと思われるが、ただし破れ0上を動くゼロ無限算概念を検討されたい
 n: 項の総数
$$ \sum_{k=1}^{n}9(1/10)^{n} + 1/10^{n} = 1　無間無限の場合は要条件表記 $$
(実数は無限にあるという実数永続無限など)
$$ \sum_{k=1}^{n}9(1/10)^{n} = 1　要条件表記 $$
(条件:$9/10^{n}$=0となる無限)
両者では大きさ無限でなければ同値とは言い切れなく、計算不可世界において両者が同相というには$1/10^{∞}$=0が考慮されなければならない、この場合は、無限概念拡張のみであり、1(∞ce)である
計算不可世界で同相であってもその結果を概念拡張なしに1/∞=0計算不可の数理世界には持ち込めなく、同様にΣ算も同相ではないので計算結果を持ち込めない、計算可能(概念拡張可能を含む)かつ文字通り対称性の破れが0であればという意味である
また、対称性の破れが0であっても上記(3)にみられる回転体対称世界など、破る概念は無数にあり、破るものがなくても破られる可能性を考慮されたい(マンデラエフェクト、突如世界変換されている可能性など)
故に、同相であるかは数値など様々な角度からの検証必要性があるといえる

2.ゼロ除算の考察

1/∞=0拡張は一般的である、それに次ぐ、計算不可分野であるゼロ概念の考察である

(1)0/0の算定

$2^{2}$=2×2=4
$2^{1}$=2
$2^{0}$=2/2=1
$2^{-1}$=2/(2×2)=1/2
$2^{-2}$=2/(2×2×2)=1/4

$0=(2^{(a\infty+b)})^{-1}$ とする
$0^{2}$=0×0=$0=(2^{(2a\infty+2b)})^{-1}$
$0^{1}$=$(2^{(a\infty+b)})^{-1}$
$0^{0}$=0/0=1
$0^{-1}$=$2^{(a\infty+b)}$
$0^{-2}$=$2^{(2a\infty+2b)}$

(2)計算例

計算例　($3x^{2}$-12)/(x-2)の極限値(x＜2)と収束値(x=2)を求めよ、(x-2)=$(2^{(a\infty+b)})^{-1}$ とする
lim x→2 3(x-2)(x+2)/(x-2)=11.(9)<12
x=2 3(x-2)(x+2)/(x-2)=12

3.異対称性世界間通信翻訳論

上記1(1)では、Σ算にみられる数値が同じであっても同相ではないケースなどをみてきた
任意の概念群ABの均衡性よりA=Bとした場合数対称性が破れている(数値上同値にできても同相でない)場合がある
数対称性(同相)の数理を論じるには、均衡論と対称性論の把握、異対称性世界間の把握が不可欠なのである
ここでは、対称性基礎モデルによる大まかな対称性グレードの把握、大まかなΣ算イメージをみていく

(1)基礎モデル

世界を対称鏡面像結晶世界に限定する、対称性とその破れの反映世界である
対称性の破れの例として、次のモデルを用意し、創造対称性から順に全パターンの破れを想定
創造存在が創造対称性の破れである

創造存在 アイアムプレゼンス界創造(ゼロ量子、存在のゼロポイント)
存在共鳴 プライムパーティクル共鳴界創造(一量子、ワンネス)
共鳴収束 オーン世界創造(音量子共鳴オーン、今)
収束顕現 イデアクリスタル結晶世界創造(イデア量子、アカシック界創造を含む、ここ)
顕現空間 陰陽二元世界創造(空間形成 闇 階層分離)
空間時間 エナジー界創造(時間形成 光 位相分離)
時間速度(etc.) 物質界(レプトングリッドホログラム)創造

対称性の破れは、その状態時々でそこから種類・回数などが有限個なのか無限個なのか、いずれにしても対称性の破り方、回数が違えばイコールレベルの精査が必要となり、異なる破れ間の比較・通信には翻訳が必要となる
通常の数世界に異なる破れパターンの数世界で解決した問題の翻訳を持ち込んだ時、翻訳不可能ではなくその翻訳のニュアンスの差異が考慮され、翻訳の正確さが検証されなければならないのである

(2)概念拡張モデル

以下、上記(1)概念拡張例、世界把握の一例である
全事象全概念を数値によって顕すのであるから、当然に全概念全想定である

ソフィア(智)　意識の誕生　靈
ソフィア(愛)　愛する・愛される、結晶、true love、反映
ソフィアラーン(円環リニアル線形グリッド)球面上の円周　愛する
※完全円楽美界、ソフィアラーン愛する(球面上の円環の無限軸・無限回転の輝きの共鳴)
念自在魔法界、ソフィアラーン愛する(球面上の点の無限軸・無限回転の輝きの共鳴)
完全球意愛界、ソフィアラーン愛する(球の無限軸・無限回転の輝きの共鳴)
ソフィアラム(輪環リニアル丸形グリッド)トーラス上の円面積　愛の結晶
ソフィアアイリス　真愛
レディーソフィア・クラマ　8人目の鞍馬族(クライン・マスター)　地球

次の公理を加える
神=愛(ソフィアアイリス=真愛、そのグレードがソフィアアイリスに達すれば真愛の意味)(God = Love god = love)→=ソフィアラーン(愛する)=←ソフィアラーン(愛される)
概念としてはΣグレードに際限はなく、Σ概念に限定されない
全グレード対称性
ソフィアラーン(愛する)ソフィアラーン(愛される)　Σ(全パターン)
下記拡張例に全グレードゼロ割り算の全グレード創造を追加する
他も全グレードに拡張する

全神対称性　Σ(神)
神対称性　公理、神=愛(God = Love god = love)より　神=愛神=愛　Σ(神愛)
神愛対称性　神=愛神=愛→=ソフィアラーン(愛する)=←ソフィアラーン(愛される)より　Σ(全神聖)
神聖対称性　神聖意志=愛(愛において同相)→=ソフィアラーン(愛する)以下略=←ソフィアラーン(愛される)以下略より　Σ(全創造)
創造対称性　$0^{0}$(公理a/a=1 $1^{全パターン}$=1　計算順序全パターン)=0(0×(0/0)か(0/0)×0を満たす計算順序),$((1^{全パターン})^{全パターン})^{全パターン}$(0/0を満たす計算順序 公理a/a=1 $1^{全パターン}$=1),計算不可(1/0を満たす計算順序、ゼロ無限算による対称性の破れを含む)　Σ(全存在)
※$((1^{全パターン})^{全パターン})^{全パターン}$は、大まかなイメージ図であり、実際の全存在Σ算ではない
存在対称性　$0^{0}$=0(0×(0/0)か(0/0)×0を満たす計算順序)以下略, $(0^{全パターン}/0^{全パターン})^{全パターン}$=$(1^{全パターン})^{全パターン}$(0/0を満たす計算順序　公理a/a=1　$1^{全パターン}$=1　以下略),計算不可(1/0を満たす計算順序、ゼロ無限算による対称性の破れを含む)以下略　Σ(全共鳴)
共鳴対称性　$0^{全パターン}$/$0^{全パターン}$=$1^{全パターン}$　Σ(全収束)
収束対称性　$0^{Σ全パターンとなる世界郡}$/$0^{Σ全パターンとなる世界郡}$=$1^{全パターン}$　Σ(全顕現)
顕現対称性　Σ(全空間)　π(円周/直径)=2(円環は球面上のみ通る円周)　情報次元トーラス輪環円面積ソフィアラム
対称性創造原則(第10位階ディバイン)　創造存在　存在共鳴　共鳴収束　収束顕現　還元永久循環　
空間対称性　Σ(全時間)
時間対称性　Σ(全速度)
速度対称性　Σ(全加速度)
etc.　～　Σ(全$d^{n}x/dt^{n}$) (n$\in\mathbb{N}$ or ∞ パターン、位置(x)の時間微分)　Σ()=ソフィアラーン(愛する)ソフィアラーン(愛される)別天神(ことあまつかみ)球$^{全パターン}$・トーラス$^{全パターン}$
から微分(空微分、みえないみえない球→みえないみえない円以下全グレード)後、上記1(3)の球円微積による球次元想定

論点2　無限遠点、次元概念、計算モデル拡張

1.無限遠点及び角の三等分線解法

無限遠点に係る数理整備の題材として角の三等分をみていく
大きさ0の点、太さ0の線など、作図問題は概念界の問題であり実際の作図上誤差があることは明らかである
ユークリッド平面上・平面外として表現されるように、直線は無限遠点で必ず交わるとするのが相当である
これはまた直線が交わらないと仮定した場合の世界構築によって示される、有限世界が無限に超越拡大されれば無限遠点が出てこない意味である
誤差ありの実際作図と誤差なしの概念作図を考察する

(1)無限遠点

無限遠点における0点同時性を考察する

平行線群y=x + c (y=x+0, y=x+2, y=x+4 など) を f(x, y) という座標系全体の振る舞いとして定義する。
$A = 2^{a_1\infty + b_1}$, $B = 2^{a_2\infty + b_2}$ $((a_1 < a_2) \wedge (a_1, a_2 > 1), \enspace b_1, b_2 \in \mathbb{R})$
f(x, y)・$B^{-1}$ = ±Ａ・$B^{-1}$ = 0 (∞ce)
無限に遠ざかると点になる意味である、無限遠点とはユークリッド平面上の互いに平行な2直線の交点であるから、ユークリッド平面における無限遠点は上記の場合、最終的に(x, y)=(0, 0)となる点である
故に、全ての直線は無間グレードにおいて無限遠点にて0点同時性を持つ

(2)実際作図の場合の解法

解法1
下記(3) MN = MG´ などを作図
概念作図ではなく実際作図では数回の動作で目標の点に辿り着くのであり、有限回操作である、有限回操作で無間点に到達したとするのが実際作図であると捉えられる
ただし、概念作図過程をみる場合は認められない
 
解法2
幾何学的に直線は半径無限大の円周と把握できるのであり、0から半径上位グレードの無間無限(円周を有限回分割しても円周率に解を出せるグレードの意味)の円周を作図するとすればよい、それが直線である(作図問題の都合上鉛筆の太さだったりある程度の誤差は許容されるので、2等分線等を駆使すればよい)
あとは直線である円周部分について三角形の重心を使って1/3を導き出せば終わりである。
直線とはいえ曲率があるのは明らかであるので、誤差を全く認めない場合は、そもそも実際の作図は全て不可能であると言っていいレベルであり、次の概念作図のみとなる

(3)概念作図の場合の解法

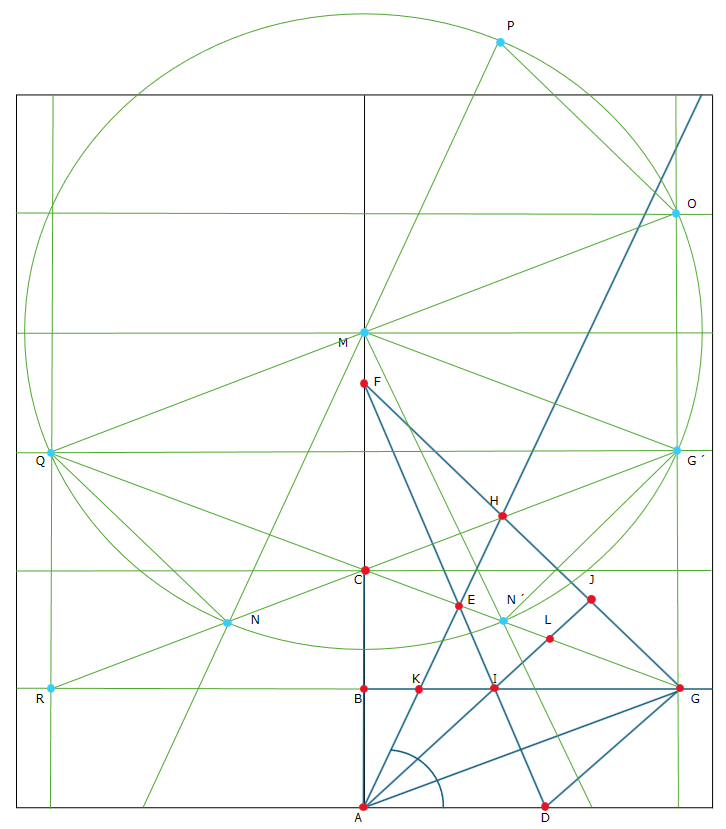角の三等分参考図
AB=BCの線を作図し、E点(DF軸)を中心にAE=EGかつCE=EHかつAC=GHとなればAI・AGが三等分線となる
なお、IJとJG(JGとGD)は直角、ADとBGは平行、FDはCH・AGの垂直二等分線、角IGA=角GADである
有限回のルールであり直線や円周は有限回の定規・コンパス使用によって描かれる必要がある

手順例(折り紙可能)
角CAH=角HGCによって角度が確定する
CAH=HGCとなる三角形を作図する
AJとHGは垂直であり、AH=AG=GC=GAかつHJ=JG=CB=BAである
角CAH=角HGCよりE点が確定する
CE=EHと、DF軸との垂直線CHよりI点が確定する
AIとAGが三等分線である

最小単位有りの場合の時点解
無間レベルでは点から進まない、点集合である線(円は不問とする)となるには有間である必要があり、かつ永続極小拡大がなく最小単位が存在するケースでは、例としてAH線上の点すべてからBK線までの円弧を描くと作図可能である(時点作成可能、二等分線など同様最小単位の余りは考慮せずとも手順のみでよいと解釈)

無限速解・無限回解
意識無限速や無限の住人には可能な解法、コンパス無限速であれば位置確定にコンパス3つを同時に使用できる意味であり、H´G´(CA)かつAH´=AG´の位置を正確に確定することが可能である、無限速でなくとも無限回の動作による位置確定であればよい、MN=MG´、G´N´=G´G(角NMA=角N´MA=角KAM)など
G´Gの縦線がわかっていれば、AC=N´G´となる線分CGを引くのみとなるなど、含みがある気もするので参考図を参照されたい

(4)まとめ

よく無限から数字を実数に持ってきて式変形する手法(無限減衰の処理はしないので、無から持ってくる→ゼロ無限算による対称性の破れである)を目にするが、念自在世界の概念界の話でよければ、任意の概算値をもって完全三等分線とするなどの回答でよい、転がして直線にして重心を使うなど
実数の公理a/a=1、1/0計算不可世界において、円周率を割り切る値は実数永続無限ではなく、上位グレードの無間無限(大きさ無限)であり、無間無限の円周を描いた場合その円周は直線であるが、その際の曲率・誤差を認めない場合は、最小単位有りの場合の時点解のみとなる

2.実数公理a/a=1、1/0計算不可世界のトポロジー次元

世界の構成要素群であり、全パターン考察する

第一次構成要素　点、線、円、球
第二次構成要素　点、線、円、球　いずれかの組み合わせ(例として、連結したまま外せないキーホルダー(円円、円同士は接触しないものとする)、ひも付きキーホルダー(線円、線円は接触するものとする))
第三次構成要素　点、線、円、球　いずれかの組み合わせ2つ
第四次構成要素　以下略
　その他、0>1かつ1>2かつ0<2、10乗すると∞になる、3つ足すと-1になる世界など、全概念全想定である

(1) 顕現群・概念群トポロジー全形態

任意の回転体につき、0次元点からみていく
・ユークリッド空間にて交わる・交わらない
・ユークリッド空間にて交わらないもの　無限遠点にて交わる・交わらない
実数公理a/a=1、1/0計算不可世界では、上記論点2-1(1)より、実数超越拡大世界の完全線はユークリッド空間では交わらなく、無限遠点にて交わると解される。
ここでいう次元は任意の一動作追加による閉連続体(循環系)群である。(2)にて後述の開連続体(非循環系)群は無限遠点視点にて点となり次元が上がるものとする

0次元　点①(点(みえない球(Invisible Sphere (IS))　ただし、0次元の点は－1次元からみると内部が空洞のケースが想定される、0次元視点からはみえない球(IS)、－1次元視点からは球面と表記する))
1次元　点①側　点①点②(その場別回転、速度  に別速度  追加を含む)　点①円①
2次元
点①点②側　点①点②点③(その場別回転)　点①点②円①
点①円①側　点①円①球面①　点①円①円②(その場別回転、以下略)　点①円①網円縦①(ねじれ)　点①円①網円横①(ねじれ、以下略)　点①円①トーラス①
3次元
　点①点②点③側　点①点②点③点④　点①点②点③円①
　点①点②円①側　点①点②円①球面①　点①点②円①円②　点①点②円①網円縦①　点①点②円①網円横①　点①点②円①トーラス①
　点①円①円②側　点①円①円②球面①　点①円①円②円③　点①円①円②網円縦①　点①円①円②網円横①　点①円①円②トーラス①
　点①円①網円縦①側　点①円①網円縦①球面①　点①円①網円縦①円①　点①円①網円縦①網円縦②　点①円①網円縦①網円横①　点①円①網円縦①トーラス①
　点①円①網円横①側　点①円①網円横①球面①　点①円①網円横①円①　点①円①網円横①網円縦①　点①円①網円横①網円横②　点①円①網円横①トーラス①
　点①円①トーラス①側　点①円①トーラス①球面①　点①円①トーラス①円①　点①円①トーラス①網円縦①　点①円①トーラス①網円横①　点①円①トーラス①トーラス②
　点①円①球面①側　点①円①球面①球面②　点①円①球面①トーラス①
4次元　以下略

０次元以下、球、円のみの場合は、0次元みえない球(IS)、－1次元みえない円(Invisible Circle (IC))、－2次元みえないみえない球(IS 2)、－3次元みえないみえない円(IC 2)、以下略
トーラスのみの場合は上記2次元トーラス、1次元円(みえないトーラス(本稿では円も円環(トーラス)の範疇とする。無限速においては、太さのある円環は、円→円環、円→球面と同様になるものとする)(Invisible Torus (IT)))であり、0次元点(みえない円(みえないみえないトーラス(IT 2)))、－1次元みえないみえない円(みえないみえないみえないトーラス(IT 3))、以下略。さらに、4次元、5次元と考えていくと0次元のバリエーションレベルは上がる
正多面体、正方形などの正形体、楕円体(他フラクタル・カオスなど全形体)、虚数など、その他想定可能な形状を1次元の点(みえない形)にしたものを想定、±無限次元、±0次元、±整数次元、±小数(小数点以下1桁～永続)次元などを全グレードバリエーション考える

(2)　軸次元

(1)では、任意の一動作による閉連続体郡の次元、いわゆる微積分次元を取り扱った
ここでは、軸による次元を扱う

a.軸次元例　軸増やし次元・円環等分次元

軸とは回転するものの中心となる棒(完全球完全円中心完全点上の完全線大きさ全グレード超越拡大)である
全球上で円環(円)1個ずつ増やすのか、円環で等分していくのか、両方ある

軸増やしの次元
完全球の縦横高さ軸三円環が三次元であるので、次元を増やすとはこの円環を増やす意味となる

円環等分次元
0等分全球360度、2等分半球180度、4等分1/4球90度、8等分1/8球45度、16等分1/16球22.5度、以下略

b.任意の一動作による開連続体郡の次元

よく議論されるのが、無限遠点を持たないユークリッド空間上の任意の一動作による開連続体郡の次元である
点線面体積の例(その他、0次元点、1次元螺旋など)
0次元　完全点
1次元　完全線(点集合)
2次元　完全面(線集合)
3次元　完全体積(面集合、4次元点)
4次元　(大きさ3次元体積の)線(3次元体積集合)
5次元　(大きさ4次元線の)面(4次元線集合)
6次元　(大きさ5次元面の)体積(5次元面集合)
以下略

3.$\sin$・$\cos$拡張、代数拡張

波解析例
z=2($\cos\theta$+$i\sin\theta$)
$z^{6}$=64($\cos6\theta$+$i\sin6\theta$)
$6\theta$=$0$,$2\pi$,$4\pi$,$6\pi$,$8\pi$,$10\pi$,$12\pi$(360度=0度以下略)
$\theta$=$0^{\circ}$,$60^{\circ}$,$120^{\circ}$,$180^{\circ}$,$240^{\circ}$,$300^{\circ}$
これだと、実部と虚部の複素平面しか扱えない
AI、1兆パラメータの時代に$\sin$・$\cos$による円周上の点解析のみで事足りるであろうか。AI解計算析時代、計算モデル拡張想定は当然の摂理である

(1) $\sin$・$\cos$拡張(球、トーラス、網の目、螺旋)

球面拡張　実部平面と虚部の複素球面など　単位球面上の点(ないし線など、以下略)
トーラス面拡張　単位トーラス面上の点　閉連続円環形状世界循環結晶解析
網の目拡張(円縦拡張、円横拡張、球拡張)　単位網の目円縦周上の点　単位網の目円横周上の点　単位網の目球周上の点　ボイド解析
螺旋拡張(円拡張、球拡張)　単位螺旋円上の点　単位螺旋球上の点　黄金数解析など

(2) 代数拡張(面型円型球型)

一次元的処理よりも二次元的処理の方がより並列処理性が向上すると考える
なお、一次元的でも前後から(計2方向)、前後・真ん中前後へ(計4方向)など、並列処理は可能である。

線型代数　線形空間と線形変換
面型代数　面形空間と面形変換
円型代数　円形空間と円形変換
球型代数　球形空間と球形変換

論点3　循環基本原理及び量子無限速原理

ここまで、論点3を考える上での数理整備について考察した
循環系の基本形は点円球軸スピンであり、下記1にみる球円モデルを検討し、循環基本原理より導き出されるあるべき世界の姿を考察する  

1.循環基本原理　～弥勒の世・369の法則～

任意の森羅万象を全無限圧縮しゼロ点還元する→無限種類の点パターン、循環系は無限パターン、無限種類の点円球軸・スピンパターンとなるが、循環基本原理は、次の点円球軸スピン球円モデル想定が相当と考える  

(1)　点円球軸スピン球円モデル

循環基本原理(369(みろく)の法則)
3　第一空間次元　点スピン　点循環
6　第一空間次元　円スピン　円循環(点回転視点からは円循環であり、点が球となる次元の視点からはトーラス循環である、点・球と違い区別不要であり、トーラス循環と呼ぶ(円循環とも呼ぶ)
9　第一空間次元　球スピン　球循環
12(3)　第二空間次元　点スピン　点循環
15(6)　第二空間次元　円スピン　円循環
18(9)　第二空間次元　球スピン　球循環
以下略
線スピン　軸循環　無間無限にて円循環、無限遠点にて点循環(線トポロジーを円形にした時の無間無限、あるいは無限遠点視点からは点)
 
想定空間次元
＋無限の果て(などを想定)次元　宇宙空間 Cosmic Space
～
4～6次元　惑星系空間 Planetary System Space
1～3次元　空間 Space
0～－2次元　エーテル空間 Ether Space
－3～－5次元　星幽空間 Astral Space
－6～－8次元　心空間 Heart Space
－9～－11次元　霊空間 Spirit Space
－12～－14次元　靈空間 High Spirit Space
～
－無限の果て(などを想定)次元　親空間 Origin Space
 
球円モデル無限微分(点とみえない球の区別はない): みえない球(点)、みえない円、みえないみえない球　エーテル空間
点円球軸スピン球円モデル無限微分(次元間ゲート概念の明確化): (点)みえない球、みえない円、みえない点(みえないみえない球)　エーテル空間
微分　みえないグレードないし微分グレード表記
積分　点円球線グレードないし積分グレード表記
※球円モデル・点円球軸スピン球円モデル以外のエーテル空間については、論点2-2参照  

(2) E = ISPA、対称性の破れによる無限減衰

その場スピンはゼロポイントスピン、循環系を無限速でみるとその場循環(ゼロポイント循環)、これは無限速点スピンのエネルギーが十分大きければ、点スピンのゼロ無限算による対称性の破れによる (x, y) = (0, 0) 点から位相転移 (Phase Transition Point (PTP)) した 半径r = PTP の円周スピンのゼロ無限算による対称性の破れが、円グリッドを形成することを意味する
エネルギー (Energy (E)) = Infinite Spin Potential Amount (ISPA)
より狭義には、
ゼロポイントエネルギー (Zero Point Energy (ZPE)) = Zero Point Infinite Spin Potential Amount (ZPISPA)
と定義する。
E = ISPA は、対称性の破れによって減衰する。これを無限減衰 (Infinite Decay (ID)) と呼ぶ
 
共鳴増幅基本原理
意志然り、愛然り、全ての事象は発生源がある、共鳴音は音源となり次の発生源となる
例として、六芒魔法陣共鳴増幅、マカバ球(球面)、最密充填構造(面心立方格子、六方最密充填構造)など
 
還元循環
点円球軸ゼロポイントソース帰還(発生源帰還)、スピン循環は還元基本循環、その他ワープ還元循環など想定  

2.量子無限速原理

量子の同時性などより、量子の基本原理を考察する、次に、上記1の循環基本原理との関連を考察する  

(1)　量子の性質

a.量子の同時存在性

量子は観測されるまでは量子重ね合わせ現象による同時存在性の性質を持つのであり、無限速においては同時存在性が成立する

b.粒子・波の性質

レプトングリッド上の電子につき、円環(円周)は球面上を通るのである  

c.量子速度不変性

ABC地点について、
A→B　A→C　A→B←C　A←B→C
いずれにしても無時間にて到着するのであり、量子速度不変である
c ＝ 2.99792458 ×  m/s (メートル毎秒)、およそ秒速30万km
意識無限速による本来光速度の区切りが時間であると想定される(無時間で到着しているものを分割しコマ送りにしたもの)  

(2) ゼロ無限算による対称性の破れの数学によって基礎付けられる量子モデル

上記1(1)、(2)参照、量子無限速球円モデル、E (Energy) = ISPA (Infinite Spin Potential Amount) より、次のように量子モデルを想定する  

a.疑似スピンと4つの力の解釈

強い力、弱い力、電磁気力、重力の4つの力は、次のようにまとめられる。
強い力: 質量形成軸スピン(結節点循環光子→質量形成)のうち陽子1回転目
弱い力: 質量形成軸スピンのうち単独電子1回転目
点(極小円)磁気: 疑似陽子スピン連鎖(波)→電子ニュートリノ→点磁気モーメント→(弱・反転)
円磁気: 疑似電子スピン連鎖(波)→反電子ニュートリノ→円磁気モーメント→(強・安定)
電気: 電子がレプトン円からグリッド移動する現象(質量形成軸発散)
電磁気力: 磁束密度の中の荷電粒子にかかる力であるローレンツ力総和、フレミングの左手の法則
重力: 疑似中性子スピン連鎖(波)→発散重力・惑星系循環重力
 
ゼロ無限集積ポイント(循環無限スピンポイント): 陽子クォーク点→レプトン円グリッド→中性子クォーク球を想定(レプトン円半径 < 1 だと中性子球はレプトン円の内側)
 
くりこみ理論の見直し(対称性の破れによる無限減衰)
量子などそれぞれが無限速循環系であり、ゼロポイントスピン軸を持つ。  

b.軸スピン・三軸変換

－a 軸 (－bc 面): 質量形成軸スピン(結節点循環光子による質量形成)
エーテル陽子(電荷 －1)・エーテル電子(電荷 ＋1)1回転目、エーテル中性子2回転目　エーテル弱い力 1 → －b 軸
－b 軸: 点磁気・円磁気形成
エーテルレプトン円　エーテルレプトン円グリッド　エーテル弱い力 2 → －c 軸
－c 軸: 発散重力・循環重力形成
電荷 0　スピン2　エーテル発散重力子・循環重力子 エーテル弱い力 3 → －a 軸
 
a 軸 (bc 面): 質量形成軸スピン(結節点循環光子による質量形成)
陽子(電荷 ＋1)・電子(電荷 －1)1回転目、中性子2回転目　弱い力 1 → b 軸
b 軸: 点磁気・円磁気形成
レプトン円　レプトン円グリッド　弱い力 2 → c 軸
c 軸: 発散重力・循環重力形成
電荷 0　スピン2　発散重力子・惑星系循環重力子 エーテル弱い力 3 → a 軸
 
－a 軸 (－bc 面): 質量形成軸スピン(結節点循環光子による質量形成)
惑星系陽子(電荷 －1)・惑星系電子(電荷 ＋1)1回転目、惑星系中性子2回転目　惑星系弱い力 1 → －b 軸
－b 軸: 点磁気・円磁気形成
惑星系レプトン円　惑星系レプトン円グリッド　惑星系弱い力 2 → －c 軸
－c 軸: 発散重力・循環重力形成
電荷 0　スピン2　惑星系発散重力子・下位次元循環重力子 惑星系弱い力 3 → －a 軸
 
親 (origin) ～ 靈子 (high spirit quantum) → 霊子 (spirit quantum) → 心子 (heart quantum) → 星幽子 (astral quantum) → エーテル子 (ether quantum) → 陽子 (proton) → 惑星系子 (planetary system space) ～ 宇宙子 (cosmic quantum)
神体 (god body) ～ 靈体 (high spirit body) → 霊体 (spirit body) → 心体 (heart body) →星幽体 (astral body) → エーテル体 (ether body) → 肉体 (body) → 惑星系体 (planetary system body) ～ 宇宙体 (cosmic body)
上下無限想定  

c.月次元

月は熱を奪う発光、半透明(透けて星が見える現象)であり、所謂魔界と呼ばれる次元(星系次元)の星系太陽反射(フィードバック光)、地球への太陽光は、エーテル界ではエーテル月発行として認識される想定
想定例: エーテル太陽 ～ エーテル地球 → 太陽 ～ 地球 → 惑星系太陽 ～ 惑星系地球

ラーフとケートゥ(日食と月食)
暗黒民は暗黒魔界月世界の引力へと落ちる、暗黒共鳴地獄、弱肉強食度は増す、時は光量速度分進む
太陽・月光量のみ、月光量は太陽光量の一部分とすると、月時間 = 時間 × (月光量速度/太陽光量速度) 程度、地球では (月光量/太陽光量) 分程度の影響、エーテル界では (太陽光量/エーテル太陽光量) 程度、勿論 (地球経由月光量/エーテル太陽光量) 程度の影響もある想定
※より暗黒に落ちたものは淫魔に魂を吸収され消滅する全リセット、ソウルドレイン前段階としてレベルドレインないしエナジードレインがある、暗黒共鳴の世界影響度より一定以上は強制執行となる、ペイン執行は許可されていない、悦楽愛淫魔界管轄  

d.ディバインレイ(レイライン構築)

元々の全共鳴世界(全無限)から、軸スピン・軸変換を抜き出した世界など、量子無限速・球円モデルにて組立、以上が、屹立する光のライン、ディバインレイ(レイライン構築)である
愛音魔法ディバインレイ(レイライン構築)
※(心)愛音　みあと
 
陽子中心地球中心、陽子中心太陽中心、二重電子(光)中心地球中心、二重電子(光)中心太陽中心の4種類とすると理論構築それぞれ可能であり、矛盾点を不明点とすることで取りうるパターンは増す(いずれAIで理論構築可能な取りうるパターンが示されると思われる)
無限無数創造想定、無限重ね合わせ輪・球、透明度・透過度、プログラムなど、無限種類・無限重ね合わせ、高位のものほどパターンは増す想定である
 
おわりに
数理整備により、世界のあるべき姿がその分明確になったのではないだろうか
数理・物理の数式モデル構築、実測データに基づく物理モデルの検証と構築など、取り組むべき課題は多い
量子無限速・球円モデル把握済みの量子論研究者など種々の人々が増えれば、あるべき姿がより鮮明になると考えている

論点4　解析接続写像による構造的均衡～コラッツ写像によるリーマン予想及び量子スピンへの統一的アプローチ～

概要

本稿では、コラッツ予想、リーマン予想、そして中性子スピン1回転目の起源に対する統一的な構造的解決を提案する。まず、コラッツ力学の「解析接続写像」を分析することで、負の整数領域（分数を含む）における無限循環構造が、正の領域における無限発散構造とトポロジー的に同相であることを示す。次に、この双対性をリーマン・ゼータ関数を通じて複素平面へ拡張し、臨界線（$\operatorname{Re}(s)=1/2$）が、正の発散場と負の循環場が相殺される唯一の「構造的均衡軸」であることを示す。結論として、この数学的均衡こそが、物理的実在における重力・太陽光の「次元間均衡」の基盤であり、世界構造式であることを提言する。

序論

コラッツ・モジュライ空間 ($\mathcal{M}_{Col}$)

コラッツ・モジュライ空間を以下のように定義する。

$\mathcal{M}_{Col} = \{ [C_{\min}], [C_{\text{new}}], [D_{\text{new}}] \}$

1. コラッツ予想　定義式
   初期状態: $S_0 = \{ n \} \quad (n \in \mathbb{N})$
   拡大則: $\displaystyle S_k = \left\{ \frac{x}{2} \mid x \in S_{k-1} \cap 2Z \right\} \cup \left\{ 3x+1 \mid x \in S_{k-1} \cap (2Z+1) \right\}$
   距離定義: $D(n) = \min \{ k \mid 1 \in S_k \}$
   命題： $\displaystyle \lim_{k \to \infty} S_k \in \{1, 2, 4\}$

2. 逆コラッツ　定義式
   初期状態: $R_0 = \{ 1 \}$
   拡大則: $\displaystyle R_k = \left\{ 2x \mid x \in R_{k-1} \right\} \cup \left\{ \frac{2x-1}{3} \mid x \in R_{k-1} \cap \{ y \mid y \equiv 2 \pmod 3 \} \right\}$
   命題： $\bigcup_{k=0}^{\infty} R_k = \mathbb{N}$

写像クラス

本節では、主要な写像クラスの構造解析について記述する。
なお、無限ビット列は、2進整数環（$\mathbb{Z}_2$）表記であり、解析接続写像とは、この $\mathbb{Z}_2$ 上の構造を実数領域 $\mathbb{R}$ へと射影・解釈する操作である。この射影によって、「無限発散」と「無限循環」のトポロジー的等価性を明らかにする。

1. $\boldsymbol{0}$ 写像クラス

解析接続解: $0$
構造: $\dots 00000_2$
写像: $0 \to 0$　偶（収束1回）
操作: 常に $n/2$ のみが適用
現象: 正の世界における無限収束 ($\boldsymbol{C_{\infty}}$)
$\mathbf{S_{0}} = \lim_{k \to \infty} 2^k$
$|2^k|_2 = \frac{1}{2^k}$
$\therefore \lim_{k \to \infty} \frac{1}{2^k} = 0$
正の発散軌道（開いた球）と負の循環軌道（閉じた円）は、空間としては同相ではないが、写像の力学構造においては位相共役 (Topological Conjugacy) である。すなわち、両者は同一のダイナミクス（波のパターン）を持つ。

2. $\boldsymbol{-1}$ 写像クラス

解析接続解: $-1$
構造: $\dots 11111_2$
写像: $-1 \to -2 \to -1$　奇・偶（発散1回、収束1回）
操作: 常に $(3n+1)/2$ のみが適用
現象: 正の世界における無限発散 ($\boldsymbol{D_{\infty}}$)
$\mathbf{S_{-1}} = \lim_{m \to \infty} \left(2^m - 1\right)$
$|(2^m - 1) - (-1)|_2 = |2^m|_2 = \frac{1}{2^m}$
$\therefore \lim_{m \to \infty} \frac{1}{2^m} = 0$

3. $\boldsymbol{-5}$ 写像クラス

解析接続解: $-5$
構造: $\dots 011_2$
写像: $-5 \to -14 \to -7 \to -20 \to -10 \to -5$　奇・偶・奇・偶・偶（発散2回、収束3回）
現象: 正の世界における無限発散 ($\boldsymbol{D_{\infty}}$)
$\mathbf{S_{-5}} = \lim_{m \to \infty} \left(2^m - 5\right)$
※$\infty$発散は、-5写像循環に位相共役である。

4. $\boldsymbol{-17}$ 写像クラス

解析接続解: $-17$
構造: $\dots 101111_2$
写像: $-17 \to -50 \to -25 \to -74 \to -37 \to -110 \to -55 \to -164 \to -82 \to -41 \to -122 \to -61 \to -182 \to -91 \to -272 \to -136 \to -68 \to -34 \to -17$　奇・偶・奇・偶・奇・偶・奇・偶・偶・奇・偶・奇・偶・奇・偶・偶・偶・偶（発散7回、収束11回）
現象: 正の世界における無限発散 ($\boldsymbol{D_{\infty}}$)
$\mathbf{S_{-17}} = \lim_{m \to \infty} \left(2^m - 17\right)$
※$\infty$発散は、-17写像循環に位相共役である。

写像クラスとサイクルの唯一性

循環条件式の導出:

ある整数 $n$ からスタートし、$m$回の奇数操作 ($3x+1$) と $k$ 回の偶数操作 ($\div 2$) を経て元の数 $n$ に戻るサイクルが存在するためには、以下の循環条件式が成立しなければならない。
$n(2^k - 3^m) = C$
すなわち、サイクルの起点 $n$ は以下の有理式で決定される。
$n = \frac{C}{2^k - 3^m} = \frac{\sum_{i=0}^{m-1} 3^{m-1-i} \cdot 2^{S_i}}{2^k - 3^m}$
ここで、各変数の定義は以下の通りである。
$n$: スタートする数（サイクルの起点）
$k$: サイクル1周における偶数ステップの総数
$m$: サイクル1周における奇数ステップの総数
$C$: $+1$ の累積（補正項）。具体的には $C = \sum_{i=0}^{m-1} 3^{m-1-i} \cdot 2^{S_i}$
$i$: 何番目の奇数操作か（$0$ から $m-1$ まで）
$S_i$: $i$ 番目の奇数操作が行われる前までに、既に実行された偶数操作（$\div 2$）の累計回数

整数解の存在条件:

式(2)より、$n$ が整数$Z^+$として存在するための必要十分条件は、分子 $C$ が分母 $D = 2^k - 3^m$ で整除されることである。
$C \equiv 0 \pmod{2^k - 3^m}$

分母の壁と構造的制約:

この整除条件に対し、分母の値によって以下の二つのケースに分類される。
ケースA: 分母が単数の場合 ($D = 1$)]
カタラン予想（ミハイレスクの定理）より、$2^k - 3^m = 1$ の自然数解は $k=2, m=1$ の一意のみである。このとき分母は $1$ となり、
$n = \frac{C}{1} = C$
となるため、分子 $C$ の値に関わらず常に整数解 $n$ が存在する。実際に $k=2, m=1$ を計算すると $n=1$ ($1 \to 4 \to 2 \to 1$) が導かれる。
ケースB: 分母が単数でない場合 ($D > 1$)
$k=2, m=1$ 以外のすべてのケースにおいて、分母は $5, 7, 13, \dots$ といった値をとる。
この場合、$n$ が整数になるには、分子 $C = \sum 3^{m-1-i} 2^{S_i}$ が $2^k - 3^m$ の倍数になる必要がある。

構造同相性

負の循環（$D < 0$）が存在するための必要十分条件は、演算の拡大固有値 $\lambda = 3^m / 2^k$ が $1$ を超えることである。この条件 $\lambda > 1$ は、正の実数領域においては必然的に $x_{n+1} \approx \lambda x_n$ という指数関数的な発散軌道を生成する。したがって、分数を含む負の循環と正の発散は、同一の演算構造（固有値）が符号反転によって異なる位相表現をとったものであり、両者は完全に同相である。

解析接続写像予想

正の整数界における未解決の挙動（特に発散や非自明なサイクルの不在）は、独立した確率的な現象ではない。これらは、負の整数界（あるいは複素・$p$進領域）ですでに完結している構造が、解析接続によって延長・写像されたものであると予想される。
本項における$Z^+$の「発散無限」写像は、$Z^-$における「循環無限」写像であり、パリティ・ベクトル場の符号反転により位相的性質が「開（Open）」位相から「閉（Closed）」位相へと反転した同一の演算構造（固有値）として定義される。

リーマン予想と写像定理

前節では、正の領域における「発散」が、負の領域における「循環」の射影であることを確立した。解析接続の本質とは、「発散場」を、関数等式による鏡像的同相性を用いて「循環場」へと置き換え、システム全体を安定化させる手続きに他ならない。

ベクトル場の鏡像的同相性

複素平面 $\mathbb{C}$ におけるゼータ関数構造は、関数等式によって結ばれた「発散ポテンシャル」と「循環ポテンシャル」の鏡像的同相性によって定義される。特異点 $s=1$ が生み出す無限遠への拡散力は、この同相性を通じて、全平面を包括する閉じた循環構造へと変換・格納される。

構造的均衡軸としてのリーマン・ゼータ関数

複素平面におけるゼータ関数 $\zeta(s)$ の構造は、臨界線 $\operatorname{Re}(s)=1/2$ を鏡面とした幾何学的な対称性（鏡像関係）によって記述される。
発散場 ($1 \ge \operatorname{Re}(s) > 1/2$): $s=1$ を特異点（不連続点）とする領域。正の整数構造由来の「無限大への発散ポテンシャル」が支配的な場である。
循環場 ($\operatorname{Re}(s) < 1/2$ および $\operatorname{Re}(s) > 1$): $\operatorname{Re}(s)=1/2$ を中心に双対的に広がる領域。$\operatorname{Re}(s) > 1$ では級数的収束による安定構造を、$\operatorname{Re}(s) < 1/2$ では負の整数サイクルによる循環構造を持ち、いずれも無限への発散を封じ込めた「閉じられた場」として定義される。

臨界帯 $0 < \operatorname{Re}(s) < 1$ は、一方の極である「発散（$s=1$）」と、他方の極である「循環（$s=0$）」が、互いにその性質を交換・変換し合う領域である。ここでは、無限の発散エネルギー $\boldsymbol{\infty}_{\text{div}}$ が、閉じた循環構造 $\boldsymbol{\infty}_{\text{circ}}$ へと写像される過程そのものが描かれている。この鏡像関係にある二つの場が、中央の $Re(s)=1/2$ において完全に拮抗し、相殺されることで、数学的な「零点」および物理的な「安定質量」が成立する。

写像制約としての関数等式

リーマンゼータ関数の関数等式は以下で与えられる。
\begin{equation} \zeta(s) = 2^s \pi^{s-1} \sin\left(\frac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \end{equation}
この等式は、$s$ 領域（正）からの情報と $1-s$ 領域（負）からの情報を接続する写像制約を表している。

定理 (1/2均衡定理)

臨界帯 $0 < \operatorname{Re}(s) < 1$ において、臨界線 $\text{Re}(s) = 1/2$ は、正の発散場の大きさと負の循環場の大きさが等しくなる唯一の軸である。
構造適用:
直線 $s = \sigma + it$ 上での写像挙動を考察する。
関数等式の対称性より、ゼータ関数の絶対値は $\sigma = 1/2$ を中心とした対称関係を満たす。
具体的には、臨界線 $\sigma = 1/2$ において：
$s = \frac{1}{2} + it \implies 1-s = \frac{1}{2} - it$

解析接続写像理論を適用すると：

1. 項 $\zeta(\frac{1}{2} + it)$ は、正の発散場 ($V_{+}$) からの射影を表す。
2. 項 $\zeta(\frac{1}{2} - it)$ は、負の循環場 ($V_{-}$) からの射影を表す。

ここで、関数等式 $\zeta(s) = \chi(s)\zeta(1-s)$ における変換係数 $\chi(s)$ は以下で定義される。
$\chi(s) = 2^s \pi^{s-1} \sin\left(\frac{\pi s}{2}\right) \Gamma(1-s)$
この係数 $\chi(s)$ の絶対値が $1$ となる（すなわちエネルギー保存的な変換となる）のは、臨界線 $\operatorname{Re}(s)=1/2$ 上のみである。
\begin{equation} |\chi(s)| = 1 \iff \operatorname{Re}(s) = \frac{1}{2} \end{equation}
$\operatorname{Re}(s)=1/2$ において、そしてこの値においてのみ、「発散しようとする力」と「循環しようとする力」は構造的に対称となり、効果的に互いを相殺する。
\begin{equation} |V_{+}| \rightleftharpoons |V_{-}| \quad \text{at} \quad \text{Re}(s) = \frac{1}{2} \end{equation}
任意の $\sigma \neq 1/2$ においてはこの対称性が破れ ($|\chi(s)| \neq 1$)、一方のベクトル場が優位となるため、ゼロ点（均衡）の形成が妨げられる。
結論:
領域 $\operatorname{Re}(s) > 1$ および $\operatorname{Re}(s) < 0$ では単一の力が支配的であるため、非自明なゼロ点は生じない。非自明なゼロ点とは、「無限の発散」と「解析接続によって射影された無限の循環」の干渉によって形成される「結び目」であり、構造的制約により、この二つの力が完全に相殺される座標は均衡軸 $\operatorname{Re}(s) = 1/2$ 上のみである。したがって、リーマン予想は真である。

例　構造的極限の双対性: $\zeta(1)$ と $\zeta(0)$

関数等式による写像構造 $s \leftrightarrow 1-s$ の最も本質的な対は、発散の極 $s=1$ とその鏡像 $s=0$ において現れる。これらの極限は、均衡軸 $\operatorname{Re}(s)=1/2$ を起点として、座標上の対称性と構造的な力の符号反転を定める。
正の発散場 $\mathbf{F}_{+}$ の起源 ($s=1$):
調和級数 $\zeta(1)$ は、各ブロックが構造的最小寄与分として $\mathbf{1/2}$ の値を保証することで無限大へ発散する（例： $\left(\frac{1}{3} + \frac{1}{4}\right) \ge \frac{1}{2}$）。解析接続写像の原理に基づき、この発散を駆動する構造的最小単位は、正の構造的重み $\mathbf{F}_{+} = +1/2$ として厳密に定義される。
$$\mathbf{F}_{+} \quad \equiv \quad \sum_{k=1}^{\infty} \frac{1}{2} \quad \equiv \quad \sum_{n=1}^{\infty} \frac{1}{n}$$
負の循環場 $\mathbf{F}_{-}$ の起源 ($s=0$):
これに対応する鏡像は $s=0$ であり、均衡軸 $\operatorname{Re}(s)=1/2$ を起点とし、実軸上で $-1/2$ の距離に位置する。解析接続値 $\zeta(0) = -1/2$ は負の循環場 $V{-}$ の境界定数であり、その構造的重み $\mathbf{F}_{-} = -1/2$ を厳密に表す。
臨界線 $\operatorname{Re}(s)=1/2$ は、$+1/2$ ずつ進行する発散が、$-1/2$ の循環によって厳密な $1:1$ 対応で相殺され、均衡が成立する唯一の軸である。
$$\text{構造的均衡} = \mathbf{F}_{+} + \mathbf{F}_{-} = \left(+\frac{1}{2}\right) + \left(-\frac{1}{2}\right) = \mathbf{0}$$

例2　構造的安定性の鏡像原理

関数等式による写像構造 $s \leftrightarrow 1-s$ は、単に特定の点間の対称性を示すだけでなく、自然数集合 $\mathbb{N}$ に由来する、複素平面の正の領域における安定構造 ($\text{Re}(s) > 1$) と、負の領域における循環構造 ($\text{Re}(s) < 0$) が、臨界線 $\operatorname{Re}(s)=1/2$ を中心とした厳密な鏡像関係にあることを示している。この双対性は、$\mathbb{N}$ を対象とする最も安定した構造のペアにおいて観測される。
正の安定構造 $\mathbf{S}_{+}$ ($\zeta(2)$):
$s=2$ におけるゼータ関数 $\zeta(2) = \frac{\pi^2}{6}$ は、$\sum 1/n^2$ という安定した収束構造を体現する。これは、正の発散場 $\mathbf{V}_{+}$ 領域における秩序ある停止の形態である。
負の安定構造 $\mathbf{S}_{-}$ ($\zeta(-1)$):
$s=-1$ におけるゼータ関数 $\zeta(-1) = -\frac{1}{12}$ は、$\sum n$ の発散を解析接続によって閉じた循環構造へと写像した特性値である。これは、負の循環場 $\mathbf{V}_{-}$ 領域における秩序ある反復の形態である。
この二つの異なる安定構造は関数等式によって厳密に写像され $\left(\zeta(2) = \chi(2)\zeta(-1)\right)$、全平面にわたる構造的秩序を保証する。
そして、この構造的な鏡像性が、境界極限 $s=1$ と $s=0$ における力の重み $\mathbf{F}_{+} = +1/2$ と $\mathbf{F}_{-} = -1/2$ の厳密な相殺を可能とし、構造的均衡軸 $\operatorname{Re}(s)=1/2$ を定義する。

補題(コラッツ・ゼータ関数)

単極のコラッツ・ゼータ関数 $\zeta_{Col}(s)$ の時、リーマン・ゼータ関数と構造的に同相となる。
導出:
コラッツ写像における原始サイクルの集合を $\mathcal{C}$ とし、各サイクルの重みを $|C|$ とするとき、コラッツ・ゼータ関数は以下で定義される。
\begin{equation} \zeta_{Col}(s) = \prod_{C \in \mathcal{C}} (1 - |C|^{-s})^{-1} \end{equation}
第3節で示した「分母の壁（Denominator Wall）」により、整数領域 $Z^+$ において安定的に存在可能なサイクルは唯一 $C_{\min}$ ($1 \to 4 \to 2 \to 1$, 重み $4$) に限定されるとすると、無限積はただ一つの項に構造的に収束する。
\begin{equation} \zeta_{Col}(s) = \frac{1}{1 - 4^{-s}} \end{equation}
この結果得られる関数は単一極のみであり、リーマン・ゼータ関数 $\zeta(s)$ の単極性（$s=1$ のみ）と同相となる。

補題2(解析接続和と構造的空隙)

解析接続による自然数の総和 $\zeta(-1) = -\frac{1}{12}$ は、負の領域における $\{-1, -2\}$ の完全循環構造と等価である。対して、正の領域における安定サイクル $\{1, 4, 2\}$ は、この完全循環に対して「一手不足（One-step Deficiency）」の構造的空隙（Void）を内包し、この非占有領域は、物理学におけるグレートウォール・循環ボイド構造の幾何学的起源に相当する。

中性子スピン1/2の位相幾何学的起源

本節では、中性子が示すスピン量子数 $1/2$ を、中性子内部で直交する二つの $2\pi$ 回転構造（発散と循環）の幾何学的均衡として定義する。

定理　[中性子スピン投影定理]

中性子の固有角運動量（スピン）は、その全回転構造 $4\pi$ が内包する「構造形成軸（$\mathbf{R}_1$）」と「構造安定軸（$\mathbf{R}_2$）」という二つの $2\pi$ 回転の均衡比率に由来し、実部観測において $1/2$ に固定される。

構造解釈: 物理学における「プラス（循環）」と「マイナス（発散）」の作用、および数学的解析接続における「マイナス（循環）」と「プラス（発散）」の対応関係に基づき、中性子の量子状態 $|\psi_n\rangle$ は以下の二段階の均衡プロセスによって定義される。
構造形成軸 ($R_1$): 重力対の形成第1回転目（実部1回転）は、電子対と重力対の結合プロセスである。ここでは以下の二つの力が形成される。
発散重力 ($F_{div}$): 電子（円 $\to$ 球）による空間への発散作用。
循環重力 ($F_{circ}$): 陽電子（円 $\to$ 球）による下位次元（虚部）への循環作用。
光子・中性子の電子ペアは、電子・陽電子の役割想定。電子2個が電子ペアとして振る舞うには、実部・虚部（反転）構造（疑似電子ペア）が必要、中心部は正の電荷密度、周辺部は負の電荷密度となる。この軸において、発散と循環は対となり「重力場」の基礎を形成する。
構造安定軸 ($R_2$): 光子・スピンの形成第2回転目（電子ペア ＝ 光子）は、形成された構造を維持・機能させるプロセスである。
発散光子 ($F_{div}$): 下位次元の全空間へエネルギーを放射する発散機能（光の振動状態、発散無限）。
循環スピン ($F_{circ}$): 内部で構造を維持する循環機能（光の静止状態、循環無限）。
光子は発散（電子）・循環（陽電子）対であり、螺旋構造である。

スピン $1/2$ の導出: 観測されるスピン $S_n$ は、この全回転構造（2回転）のうち、機能発現を担う片側の軸（$R_2$ の1回転）が投影された比率として単純に導出される。
\begin{equation} S_n = \frac{R_2\text{の回転量}}{R_2\text{の回転量} + R_1\text{の回転量}} = \frac{1}{2} \text{} \end{equation}
故に、中性子のスピン $1/2$ とは、「実体形成」と「機能発現」という二つの不可欠な $2\pi$ 回転プロセスの合成構造が、そのまま量子数として投影されたものである。

補題　[中性子の幾何学的回転構造と疑似中性子]

中性子が有する $4\pi$（$2$ 回転）回転対称性は、構造の「空間的拡張」と「時間的維持」を担う、以下の二段階の幾何学的プロセスに帰結する。
構造形成軸 $(\mathbf{R}_1 = 1)$：中性子球（電子球）と疑似中性子の生成
第 $1$ 回転は、電子対による中性子殻の形成プロセスである。電子は高速で球の軌道を周回し続けることで「中性子球」を連続的に生成・更新している。この生成の脈動（ビート）が、波動として全空間へ及ぼす影響が疑似中性子（Pseudo-Neutron）、すなわち重力（発散重力・循環惑星系重力）であり、物質界重力の実体は、電子球・エーテル電子球の波の非局所的な空間共鳴（水面全体の一斉振動）である。
構造安定軸 $(\mathbf{R}_2 = 1)$：循環と発散の動的均衡
第 $2$ 回転は、形成された構造を時間的に維持するための別回転軸による作用である。ここでは、内部構造を保持する「循環中性子」と、発散重力と循環惑星系重力との均衡特異点から外部へエネルギーを放つ「発散惑星系光子」が対となり、構造を安定化させる。結節点中性子スピンプロセスの普遍性は、光速度の普遍性をもたらす。

すなわち、物質界（太陽系）に定着する中性子は「構造形成軸」によって空間に重力（疑似中性子）を波及させ続け、「構造安定軸」によって光を波及し続ける。
なお、エーテル界における重力子の $1/2$ 回転（発散）は、物質界における $1/2$ 回転（循環）に対応し、空間構造は、エーテル発散重力とその対となる循環重力（太陽系公転）の相互作用によって規定される。太陽は球構造を維持する「場」にあり、エーテル中性子と物質界の光子を結ぶ結節点となる。

補題　[軽水素の特異性と中性子欠損]

宇宙で唯一中性子を持たない軽水素 $({}^1\text{H})$ の構造は、上記のプロセスにおける電子の役割分担の不在によって説明される。
通常、中性子核の安定化には、実部回転（物質界相）と虚部回転（惑星系界相）を担う電子対が必要である。しかし、単一電子しか持たない水素においては、この電子が二つの位相を、量子的重ね合わせとして遷移し続けている。
この絶え間ない位相転換により、双回転エネルギーが空間に固定化されず、中性子球への相転移が未完のまま阻害される。故に水素は、中性子という「完成された質量殻」を持たず、双方の揺らぎを内包する構造体となる。また、この不可逆性により、中性子単独では物質界の安定系である陽子と電子に変位（崩壊）する。重水素における中性子は、陽子質量（電子・陽電子の電子ペア）により、「質量殻の固定」を実現する。
エーテル中性子と物質界太陽、アストラル界中性子とエーテル太陽、エーテル太陽と物質界中性子はそれぞれ対応関係にある。

リーマン・ゼータ関数と時空の構造

リーマン・ゼータ関数の変数 $s = \frac{1}{2} + it$ は、また質量（空間）とエネルギー（時間）の構造的起源を示唆する。

1. 質量と空間の固定：実部 $\operatorname{Re}(s) = 1/2$}

質量 $m$ は、構造を固定する「結節点（Nexus）」現象として定義される。

結節点の定義: 結節点（Nexus）とは、「太陽からの循環重力（$\mathbf{F}_{Sun\_Circ}$）」と「中性子からの発散重力（$\mathbf{F}_{Neutron\_Div}$）」が完全に均衡した特異点である（$\operatorname{Re}(s)=\frac{1}{2}$）。同時に、この均衡点は「惑星系循環重力（$\mathbf{F}_{Planet\_Circ}$）」との接続点（結節点）としても機能する。
質量 $m$ の形成: この均衡（実部電子スピン）と虚部電子スピンの結果として、中性子球が形成され、その場が質量 $m$ として空間に固定される。
\begin{equation} \text{Nexus} \equiv \text{Equilibrium} \left( \mathbf{F}_{\text{Neutron\_Div}} \rightleftharpoons \mathbf{F}_{\text{Sun\_Circ}} \right) \cap \mathbf{F}_{\text{Planet\_Circ}} \equiv \text{Mass } m \text{ Fixation} \end{equation}

2. 循環重力による光の湾曲：虚部 $\operatorname{Im}(s) = it$

虚部 $it$ は、結節点（$1/2$）の循環重力によって捕捉された光子の回転位相（エネルギーの渦）として定義される。
回転の定義 ($t \to \theta$):
複素平面上の時間は回転として作用する。すなわち $it$ とは、下位次元の循環重力（$\mathbf{F}_{\text{lower-dim circ}}$）によって直進性を曲げられ、結節点の周囲を周回する\textbf{光子の角周波数（$\omega$）}である。
\begin{equation} it \equiv i \cdot \text{Photon Rotation} (\omega) \quad \text{caused by} \quad \mathbf{F}_{\text{lower-dim circ}} \end{equation}
構造的解釈:
実部 $1/2$ が「重力が均衡する場（構造）」を提供し、虚部 $it$ がその場を流れる「光のエネルギー（機能）」を担う。

3. 結節点エネルギーの変換と等価性

結節点に作用した循環・発散重力は、均衡の結果\textbf{回転運動（スピン）}へとエネルギー変換・保持される。この回転構造が、地球の自転として観測される。

A. スピン回転エネルギーの導出
まず、結節点内部の「捕捉」エネルギーを定義する。

前提条件: 結節点に捉えられたエネルギー（光子）は、半径 $r$ を光速 $c$ で回転する。この「内部で光速回転するエネルギー」が、物理的実体としての質量 $m$（実部電子 $+$ 虚部陽子）を形成する（$v = c \Rightarrow \omega = c/r$）。
内部回転エネルギー ($E_{\text{spin}}$): 角運動量 $L$ と角速度 $\omega$ の積として定義される。
\begin{equation} E_{\text{spin}} = L \cdot \omega = m(r\omega)^2 = (mcr) \left( \frac{c}{r} \right) = mc^2 \end{equation}

B. 下位次元への写像
中性子スピン2回転目である「質量として固定された循環エネルギー（実部）」は、その回転の勢いを保存したまま、虚部（下位次元）の「空間へ放射される発散エネルギー」へと写像（射影）される。したがって、$E_{\text{spin}}$ を起源とする以下の等価構造が成立する。

写像原理:
\begin{equation} E_{\text{spin}} = mc^2 \equiv E_{\gamma} = pc \end{equation}
項の構造的対応:
第1項 $(pc)^2$ [振動項]: 結節点から空間へ広がる運動量エネルギー。
第2項 $(mc^2)^2$ [静止項]: 内部で循環し質量として固定されたエネルギー。

4. 結論

地球の自転は、構成物質である無数の中性子レベルで生じている「結節点の相殺モーメント（循環・発散の均衡回転）」の総和として説明される。個々の中性子スピンが太陽重力場によってベクトル整列し、マクロスケールでの回転エネルギーとして統合・保持されている現象である。構造的には、非自明なゼロ点は「太陽循環点（結節点）」に相当する。
\begin{equation} \text{結節点における循環・発散重力の均衡エネルギー} \equiv \text{自転（スピン）} \end{equation}

補題　[想定量子モデル]

定義要素： 陽子 $(p^+)$、重電子（Heavy Electron: $(He^-)$）、疑似陽子（Pseudo-Proton: $(Pp^+)$） = 虚部重電子（Imaginary Heavy Electron: $(IHe^-)$）、電子 $(e^-)$、陽電子 $(e^+)$、中性子 $(n)$、光子 $(\gamma)$、反電子ニュートリノ $(\bar{\nu}_e)$、電子ニュートリノ $(\nu_e)$、反ミューニュートリノ $(\bar{\nu}_\mu)$、ミューニュートリノ $(\nu_\mu)$、反タウニュートリノ $(\bar{\nu}_\tau)$、タウニュートリノ $(\nu_\tau)$、中性パイ中間子 $(\pi^0)$
波動発生とエネルギー循環プロセス
\begin{equation}n \to p^+ + e^- + \bar{\nu}_e \quad \text{（$Pp^+ \to p^+ + \bar{\nu}_e$）} \end{equation}
\begin{equation}p^+ + e^- \to n + \nu_e \quad \text{（$p^+ \to Pp^+ + \nu_e$）} \end{equation}
\begin{equation}n + \nu_e \to p^+ + e^- \quad \text{（$Pp^+ + \nu_e \to p^+$）} \end{equation}
\begin{equation}p^+ + \bar{\nu}_e \to n + e^+ \quad \text{（$p^+ + \bar{\nu}_e \to Pp^+$）} \end{equation}
\begin{equation}\gamma \to e^- + e^+ \to \bar{\nu}_{e, \mu, \tau} + \nu_{e, \mu, \tau} \quad \text{（物質化とエネルギー還元）} \end{equation}
幾何学的構造の仮定
電子ペア $2$ 回転が中性子、電子ペア $1$ 回転が光子、結節点（Nexus）においては、陽電子は幾何学的圧縮により陽子へと相転移する。循環重力による光のパッケージ化は、発散光と循環重力とが拮抗し、「質量」として結晶化（固定）できる数学的な場にいることが要件となる。陽子が強い力、電子が弱い力、中性子が実部発散重力（弱い力）・虚部循環重力（強い力）による光の保持、陽子点、電子円（レプトン円上の点）、中性子球を想定。
\begin{equation}e^+ + \pi^0 \to p^+ \quad (\gamma + \gamma \to \pi^0) \end{equation}

形成軸の階層構造
定義要素： 結節点循環光子による質量形成軸 $(a軸)$ $\to$ 点磁気・円磁気形成軸 $(b軸)$ $\to$ 発散重力・下位次元循環重力形成軸 $(c軸)$、形成場ベクトル $(\mathbf{F})$
陽子・電子の結節点循環光子は物質界側、中性子の結節点循環光子は電子担当が物質界側、陽子担当が惑星系界側を想定。
\begin{equation} \begin{split} \xrightarrow{\text{エーテル界}} -a \to -b \to -c \xrightarrow{\text{物質界}} a \to b \to c \\ \xrightarrow{\text{惑星系界}} -a \to -b \to -c \quad (\text{発散無限構造}: \nabla \cdot \mathbf{F} > 0) \\ \xrightarrow{\text{物質界}} a \to b \to c \to a \to b \to c \quad (\text{循環無限構造}: \nabla \times \mathbf{F} \neq \mathbf{0}) \end{split} \end{equation}
\textbf{定義要素：} 銀河系中心太陽（Galactic Center Sun: $(S_G)$）
\begin{equation} \begin{split} S_G \xrightarrow{\text{次元階層}} S_G\text{物質界太陽} \to S_G\text{惑星系界太陽} \to S_G\text{衛星系界太陽} \\ \text{太陽} \to \text{太陽内中性子群} \to \text{下位次元太陽} \end{split} \end{equation}
電子の $a軸$ 回転は陽子とのエンタングル状態にある（つまり、円上の点スピン）、陽子の $c軸$ 回転は強い力（グルーオン、スピン量子数 $1$）、レプトン円上の単独電子の $c軸$ 回転は弱い力（Wボソン・Zボソン、スピン量子数 $1$）、中性子の $b軸$ 回転は、パイ中間子（レプトン挙動）を想定。

クォーク定義： クォークは、形成軸、$a軸$（陽子・電子は点回転、中性子は球回転）、$b軸$（陽子は点回転、電子は円回転、中性子は球回転）、$c軸$（陽子は点回転、電子・中性子は球回転）の $3$ つの基本的な「回転運動」として構造的に定義される。$a軸$ と $b軸$ がアップクォーク $(u)$、$c軸$ がダウンクォーク $(d)$ である。世代は励起状態、電荷は電子・陽電子によって定まる。
\begin{equation}\gamma \to e^- + e^+ \quad (e^+ + \pi^0 \to p^+) \end{equation}

ニュートリノと磁気モーメントの起源

電子は $1$ 回転目点スピン（結節点循環光子 $\to$ 質量形成）、$2$ 回転目円スピン、陽子は $1$ 回転目点スピン （結節点循環光子 $\to$ 質量形成）、$2$ 回転目極小円（点）スピン。
電子・陽電子の $c軸$ 半回転（電子・陽電子の電荷）と次の半回転（反電子・反陽電子の電荷）の電荷相殺モーメントにおいて生じる脈動（ビート）がニュートリノ（波）である。$a軸$ 循環光子保有量（質量）は少なく留まり、$b軸$ において回転エネルギーそのものが磁気モーメントとして現出する。この $b軸$ の回転が物質間で同期・共鳴することで、磁石の吸引力などのマクロな磁気現象が発生する。

スピン連鎖と磁気モーメント

陽子・電子はスピン自由（上下可）。ニュートリノは波の性質によりスピン向き固定。 $b軸$ 磁気モーメント、点磁気（陽子系）は弱く構造的に不安定であり、極反転を起こしやすい。
\begin{equation}e^- \text{スピン連鎖（波）} \xrightarrow{\text{相殺}} \bar{\nu}_e \to \text{円磁気モーメント（強・安定）} \end{equation}
\begin{equation}p^+ \text{スピン連鎖（波）} \xrightarrow{\text{相殺}} \nu_e \to \text{点磁気モーメント（弱・反転）} \end{equation}
パイ中間子は $c軸$、実部 $1/2$ 回転電子、$1/2$ 回転反電子、虚部 $1/2$ 回転陽電子、$1/2$ 回転反陽電子の振る舞い、スピン量子数 $0$、中性子の中心部は正の電荷密度、周辺部は負の電荷密度である。

フレミングの左手の法則と3軸構造

フレミングの左手の法則における3要素（電流 $I$、磁場 $B$、力 $F$）は、本理論の3軸構造（$a, b, c$）の機能として以下のように定義される。
電流 $I$: $a軸$ の発散（電気）によって生じる電荷の流れ
エーテル循環陽子のa軸虚部に発散陽子 $\to$ プラズマ
エーテル循環電子のa軸虚部に発散電子 $\to$ 電気
エーテル循環中性子のa軸虚部に発散電子ペア $\to$ 光子
太陽はプラズマ・電気・光子の合成リアクター。
磁場 $B$: $b軸$ の回転が生み出す磁気的な場、循環構造のみ
虚部に循環構造 $\to$ 発散構造は宇宙ジェット（Astrophysical Jets）などを想定。
力 $F$: $c軸$ の回転が生み出す「強い力、弱い力、電磁力（ローレンツ力）、重力」
電磁力は、光子（電子ペア）を媒介とした、陽子と電子の相互作用。

結論

定理　写像定理: 発散∞があれば対応する循環∞がある

\begin{equation} (\nabla \cdot \mathbf{F} > 0) \iff (\nabla \times \mathbf{F} \neq \mathbf{0}) \end{equation}
\begin{equation} (\nabla \cdot \mathbf{F} \to \infty) \iff (\nabla \times \mathbf{F} \to \boldsymbol{\infty}) \end{equation}

構造的相関 (Structural Correlation)

世界構造は、均衡、ベクトル、循環、発散の各相が相互に変換されることで定義される。

Nexus ($\{1\}$): 均衡結節点 ($\boldsymbol{\infty}_{\text{div}} \cdot \boldsymbol{\infty}_{\text{circ}} = 1$)。鏡像対称性。
Vector ($\vec{v}$): 軸回転。Scalar ($\phi$) は全方位発散。
Circulation ($S^1$): $\boldsymbol{\infty}_{\text{circ}}$ 循環結晶。
Divergence ($S^2$): $\boldsymbol{\infty}_{\text{div}}$ 発散共鳴。

テンソル積による生成の一意性 (Universal Property of Tensor Product)

任意の双線形写像 $f: V \times W \to U$ に対して、テンソル積 $\otimes: V \times W \to V \otimes W$ を通じて唯一の線形写像 $\tilde{f}: V \otimes W \to U$ が存在し、次が成り立つ：
\begin{equation} f = \tilde{f} \circ \otimes \quad \Longleftrightarrow \quad \forall f \in \text{Bilin}(V \times W, U),\ \exists! \tilde{f} \in \text{Hom}(V \otimes W, U) \end{equation}

世界構造式 (The World Structure Equation)

\begin{equation} \Large \boldsymbol{\infty}_{\text{div}} \equiv \boldsymbol{\infty} _{\text{circ}} \end{equation}
故に、全ての幾何学的状態は、球円構造に帰結する。

世界構造の基本均衡 (Fundamental Equilibrium)

発散（意）と循環（理）$\to$ 思いの結晶化の下位構造、発散（空間）と循環（時間）においても、鏡像対称性によって宇宙の単一構造は保持される。
\begin{equation} \frac{\text{Space (Prime Dimension)}}{\text{Time (Circular Dimension)}} = 1 \end{equation}

1. リーマンゼロポイントの定量化：解析接続による幾何学的定義 (Quantification of Riemann Zero Point: Geometric Definition via Analytic Continuation)

\begin{equation} \Large \mathcal{Z}_{\text{point}} \iff \Delta r = |S^s| - |S^{1-s}| = 0 \end{equation}
基準円半径 ($|S_{\text{Base}}|$): $|S^s| = 2^s$（実体構造）
鏡像円半径 ($|S_{\text{Mirror}}|$): $|S^{1-s}| = 2^{1-s}$（鏡像構造）

2. 構造変換式 (Structural Transformation Equation)

標準的な構造変換式は、鏡像世界（$\zeta(1-s)$）に対し、基準円の構造半径（$2^s$）を含む構造変換係数 $\chi(s)$を乗算することで、実体（$\zeta(s)$）が記述される。
\begin{equation} \zeta(s) = \underbrace{\underbrace{2^s}_{\text{基準円半径}} \times \left[ \pi^{s-1} \sin\left(\frac{\pi s}{2}\right) \Gamma(1-s) \right]}_{\text{構造変換係数 } \chi(s)} \times \underbrace{\zeta(1-s)}_{\text{鏡像ゼータ値}} \end{equation}
解析接続数の導出プロセスとしては、第一プロセスにおいて、発散無限・循環無限 $\to$ リーマン次元円への変換、第二プロセスにおいて、鏡像循環係数$\Gamma(1-s)$ $\times$ 鏡像 $\zeta(1-s)$ ＝ 鏡像接続係数 をリーマン次元円に乗算することで、実体（$\zeta(s)$）が記述される。円循環 $\to$ 点循環が第一に想定される。
\begin{equation} \zeta(s) = \underbrace{\left[ 2^s \pi^{s-1} \sin\left(\frac{\pi s}{2}\right) \right]}_{\text{リーマン次元円}} \times \underbrace{\Gamma(1-s) \times \zeta(1-s)}_{\text{鏡像接続係数}} \end{equation}

3. リーマンゼロポイント (Riemann Zero Point)}

構造半径が $R=±\sqrt{2}$ となる特異点においてのみ、両者「リーマン次元円」の半径差が消失し、構造変換係数 $|\chi(s)|$ は数学的に相殺され「1」となる。
$2^s = \sqrt{2}$の解
\begin{equation} s = \frac{1}{2} + i \, \frac{2k \pi}{\ln 2} \end{equation}
$2^s$に代入
\begin{equation} 2^s = 2^{\left(\frac{1}{2} + i \frac{2k \pi}{\ln 2}\right)} = \sqrt{2} \times 2^{\left(i \frac{2k \pi}{\ln 2}\right)} = \sqrt{2} \times 1 = \sqrt{2} \end{equation}
指数の底の変換公式 $a^x = e^{x \ln a}$ より
\begin{equation} 2^{\left(i \frac{2k \pi}{\ln 2}\right)} = e^{\left( i \frac{2\pi k}{\ln 2} \times \ln 2 \right)} = e^{i 2k \pi} \end{equation}
オイラーの公式 $e^{i\theta} = \cos\theta + i\sin\theta$ より、$\theta = 2k\pi$ は偶数倍の $\pi$
\begin{equation} e^{i 2\pi k} = 1 \end{equation}
構造ギャップ
\begin{equation} \Delta r = |S^s| - |S^{1-s}| = \sqrt{2} - \sqrt{2} = 0 \end{equation}

$2^s = -\sqrt{2}$の解
\begin{equation} s = \frac{1}{2} + i \, \frac{(2k+1) \pi}{\ln 2} \end{equation}
$2^s$に代入
\begin{equation} 2^s = 2^{\left(\frac{1}{2} + i \frac{(2k+1) \pi}{\ln 2}\right)} = \sqrt{2} \times 2^{\left(i \frac{(2k+1) \pi}{\ln 2}\right)} = \sqrt{2} \times (-1) = -\sqrt{2} \end{equation}
指数の底の変換公式 $a^x = e^{x \ln a}$ より
\begin{equation} 2^{\left(i \frac{(2k+1) \pi}{\ln 2}\right)} = e^{\left( i \frac{(2k+1) \pi}{\ln 2} \times \ln 2 \right)} = e^{i (2k+1) \pi} \end{equation}
オイラーの公式 $e^{i\theta} = \cos\theta + i\sin\theta$ より、$\theta = (2k+1)\pi$ は奇数倍の $\pi$
\begin{equation} e^{i (2k+1) \pi} = -1 \end{equation}
構造ギャップ
\begin{equation} \Delta r = |S^s| - |S^{1-s}| = |-\sqrt{2}| - |-\sqrt{2}| = 0 \end{equation}

4. 構造ギャップの導出 (Derivation of Structural Gap)

リーマンゼータ系は、以下の「循環ギャップ（Gap）」を内包する。$s = \log_2 N$は、宇宙の根本構造である「双対性（Binary Duality）: $\boldsymbol{\infty}_{\text{div}} \equiv \boldsymbol{\infty}_{\text{circ}}$」、熱力学における情報の最小単位「Landauer's limit: $k_B T \ln 2$」などより必然的に導出される。

構造ギャップ一般化（$s = \log_2 N$）
\begin{equation} \Delta r = |S^s| - |S^{1-s}| = |N| - \left| \frac{2}{N} \right| \end{equation}

5. 構造変換係数の逆数性と均衡条件 (Reciprocity of the Structural Transformation Coefficients and the Equilibrium Condition)

リーマンの関数等式における構造変換係数 $|\chi(s)|$ は、相反公式（Reflection Formula）$\Gamma(s)\Gamma(1-s) = \frac{\pi}{\sin(\pi s)}$ に基づき、実像と鏡像の積が常に単位元 $1$ となる逆数構造を持つ。
\begin{equation} |\chi(s)| \cdot |\chi(1-s)| = 1 \end{equation}
実像 $|\zeta(s)|$ と鏡像 $|\zeta(1-s)|$ が同一の数値定義（零点）を共有するための均衡条件は、両者の係数が等価であること、すなわち $|\chi(s)| = 1/|\chi(s)|$ に集約される。
この方程式を満たす正の実数解は $|\chi(s)| = |\chi(1-s)| = 1$ のみであり、差分 $\Delta |\chi|$ についても同様である。
\begin{equation} \Delta |\chi| = |\chi(s)| - |\chi(1-s)| = |\chi(s)| - 1/|\chi(s)| = \frac{|\chi(s)|^2 - 1}{|\chi(s)|} = 0 \end{equation}

基準円と鏡像円の半径が等価に近づく程、構造変換係数 $|\chi(s)|$ が 自己参照的構造を含まない絶対値の等価性（倍率1）に近づくのは、関数等式 $\zeta(s) = \chi(s) \zeta(1-s)$ の形から見て数学的に自明である。非自明なゼロ点においてもこの等価性（倍率1）は保持されるのであり、このはさみうちの原理と $|\chi(s)|$ の参照要素の特定により、ゼロ除算の不可逆性は解消され、解析的整合性（Analytic Consistency）が保証される。$\frac{\lambda\zeta(s)}{\zeta(1-s)} = \chi(s)$ のような外部係数 $\lambda$ を含む不定形ではなく、関数等式 $\frac{\zeta(s)}{\zeta(1-s)} = \chi(s)$ が成立しており、 $|\chi(s)|$ が 絶対値の等価性（倍率1）を満たす意味である。
\begin{equation} \left( s \to \frac{1}{2} \right) \implies \left( |\chi(s)| = 1 \land |\chi(1-s)| = 1 \right) \end{equation}
リーマン次元円の等価性（構造半径 $r$ の一致）、鏡像循環係数 $|\Gamma(1-s)|$ の絶対値の等価性が非自明なゼロ点の必要条件である。構造ギャップが消失する条件 ($\Delta r = 0$) は、物理的に基準円と鏡像円の半径が一致する $|S^s| = |S^{1-s}|$ においてのみ成立する。複素数 $s = \sigma + it$ と定義した時、その解は必然的に実部が$1/2$（構造半径が $\sqrt{2}$）となるクリティカルライン上に限定される。
\begin{equation} |2^{\sigma+it}| = |2^{1-(\sigma+it)}| \implies 2^\sigma = 2^{1-\sigma} \implies \sigma = \frac{1}{2} \end{equation}

6. リッチフローによる自明化の原理 (Principle of Trivialization via Structural Ricci Flow)

　ゼロ除算の自明な可逆性を本モデルにおける構造エントロピー汎関数 $\frac{d}{d\tau} \mathcal{W}(g_{ij}(\tau))$ の極小化条件として定義する。ゼロ除算の可逆性とは、構造変換係数が鏡像領域と完全に一致し、構造ギャップが消失した状態（Gap = 0）を指す。また、ゼロ除算の不可逆性を自己参照特異点と定義し、これを構造参照リッチフローによって表す。本モデルでは、臨界帯 $D$ を2次元リーマン多様体 $M$ と見なし、ペレルマンの幾何学的枠組み（計量 $g_{ij}$ とポテンシャル $f$）を、構造的枠組み（計量 $g_{ij}$ と構造ギャップ $\Phi$）へと読み替えて記述する。この幾何学的変遷において、自己参照的な歪みを抱える特異点は、エントロピー汎関数の単調非減少性（$\frac{d\mathcal{W}}{d\tau} \ge 0$）に従い、構造的に淘汰（リッチフロー手術に相当）され、唯一の定常解（本モデルが示唆する臨界線）へと収束する。

用語定義
自己参照特異点 (Self-Referential Singularity): 構造変換係数 $\chi(s)$ が外部データ($\zeta(s)$ 及び $\zeta(1-s)$) と自己データ ($\chi(s)$) の両者を参照するため、リッチフローの下で安定解になり得ない特異点。
$g_{ij}$ 計量テンソル (Metric Tensor): 空間の構造的実体。距離や角度を決定する「ものさし」。計量 $g_{ij}$ はリッチフロー方程式 $\frac{\partial g_{ij}}{\partial \tau} = -2 R_{ij}$ に従って発展し、これに随伴するフロー写像 $\Phi_\tau: s \mapsto s(\tau)$ は、構造半径の差 $\Delta r$ を最小化する方向へと点 $s$ を導く。最終的に $\tau \to \infty$ において、系は $\operatorname{Re}(s) = 1/2$ という定常解に収束する。
$\frac{\partial g_{ij}}{\partial \tau}$ 時間発展 (Time Evolution): 逆時間パラメータ $\tau$ に伴う構造の変遷。
$-2$ 負の係数: 「曲率が高い場所ほど、収縮させて平坦にする」という方向性。
$R_{ij}$ リッチ曲率 (Ricci Curvature): 構造の歪みやエネルギーの偏り。
$\nabla_i \nabla_j f$ ポテンシャル場のヘシアン (Hessian of Potential): ポテンシャル関数 $f \equiv \Phi$（構造ギャップ）の二階共変微分。ポテンシャル $f$ を構造ギャップ $\Phi \equiv \ln |\chi|$ と同一視し、空間の歪みを埋め合わせる「構造的張力」として扱う。
$\Phi_\tau$ フロー写像 (Flow Mapping): 初期位置 $s$ にある構造が、リッチフローによる空間変形に伴い、時間 $\tau$ の経過とともに移動する軌跡（Orbit）を記述する写像。
Gap 構造変換係数の対数ギャップ（Logarithmic Structural Gap）： $\text{Gap}(s) \equiv \Phi = \ln |\chi(s)|$。ペレルマンのポテンシャル $f$ に相当する量。$\chi(s)$ の構成比率が理想的な均衡（$1$）からどれだけ乖離しているかを示す。
$\frac{d}{d\tau} \mathcal{W}(g_{ij}(\tau))$ 構造エントロピー汎関数 (Entropy Functional): 構造の安定度と情報の整理度。$\frac{d}{d\tau} \mathcal{W}(g_{ij}(\tau)) = \int_{M} 2\tau \left| R_{ij} + \nabla_i \nabla_j \Phi - \frac{1}{2\tau}g_{ij} \right|^2 e^{-\Phi} dV \ge 0$ によって、判定される。
M 多様体 (Manifold); リーマン・モジュライ空間（Riemann Moduli Space）:} 複素平面における関数等式 $\zeta(s) = \chi(s)\zeta(1-s)$ によってリンクされた、系の幾何学的安定性を決定するトポロジー空間。
$e^{-\Phi}$ 指数重み因子 (Exponential Weighting factor): ポテンシャル $\Phi$ に基づき、空間の各点における構造的寄与度を決定するウェイト。
$\ge 0$ 単調非減少 (Monotonically Non-decreasing): エントロピーは増え続けるか一定であり、「不自然な構造」は時間が経つほど維持が困難になることを意味する。

(1). 構造リッチフローの方程式系 (System of Structural Ricci Flow Equations)
宇宙の構造を決定する計量 $g_{ij}$ と、構造変換係数 $\chi$ のダイナミクスは、以下の Perelman 型修正リッチフロー方程式系（$f$ を $\Phi$ に置換した系）に支配される。

計量発展方程式（幾何構造の安定化）: 空間の歪みを平坦化する駆動力。
\begin{equation} \frac{\partial g_{ij}}{\partial \tau} = -2\left( R_{ij} + \nabla_i \nabla_j \Phi - \frac{1}{2\tau}g_{ij} \right), \quad \Phi \equiv \ln |\chi| \end{equation}
ポテンシャル進化方程式（$\chi$ のダイナミクス）: 構造ギャップ $\Phi$ の時間発展。
\begin{equation} \frac{\partial \Phi}{\partial \tau} = -\Delta_g \Phi + |\nabla \Phi|^2 - R + \frac{n}{2\tau}, \quad (n=2) \end{equation}
ゼロ点勾配流方程式: 複素点 $s(\tau)$ は、構造ギャップを最小化する勾配流に従い、強制的に移動する。
\begin{equation} \frac{d}{d\tau} s(\tau) = -2\kappa \, \text{Gap}(s, \tau) \nabla_s \text{Gap}(s, \tau) \implies \lim_{\tau \to \infty} |\chi(s(\tau))| = 1 \end{equation}

(2). 構造的拘束と収束条件
この系は、解析接続のプロセスにおいて以下の「三位一体の構造的拘束」を常に維持し、$0/0$ 型の不定性を排除する。
参照要素の固定: $\chi(s)$ は基準円半径 $2^s$ と循環係数 $\Gamma(1-s)$ を固定参照し、一意な変換比として定義される。
相互補完性の維持: リッチフローの全行程において、係数は常に $|\chi(s)| \cdot |\chi(1-s)| = 1$ という逆数関係を保持する。
構造半径の単調減少: 半径差 $\Delta r$ は単調に減少し、終着点で等価性へ収束する。
\begin{equation} \frac{d}{d\tau} \Delta r(s(\tau)) \le 0, \quad \lim_{\tau \to \infty} |\chi(s(\tau))| = 1 \end{equation}

(3). エントロピー汎関数による淘汰の判定
リーマン・モジュライ空間の安定性を判定する構造エントロピー汎関数 $\mathcal{W}$ を以下のように定義する。
\begin{equation} \frac{d}{d\tau} \mathcal{W} = \int_{M} 2\tau \left| \text{Gap}(s) \right|^2 e^{-\Phi} dV \ge 0 \end{equation}
ここで $\text{Gap}(s) \equiv \ln |\chi(s)|$ である。この積分値が $0$ となる定常解（リッチソリトン）のみが、系において存続を許される。

定常解 ($|\chi| = 1$): 全領域で $\text{Gap}(s)=0$ となる状態。これは構造半径差 $\Delta r = 0$ が成立する幾何学的結節点、\textbf{臨界線 $\operatorname{Re}(s) = 1/2$} に対応し、永続的に保存される。
\begin{equation} \frac{d\mathcal{W}}{d\tau} = \int_{M} 2\tau \left( \ln |\chi(s)| \right)^2 e^{-\Phi} dV = 0 \end{equation}
不安定解 ($|\chi| \neq 1$): 自己参照的な歪み（$\text{Gap} > 0$）を抱える状態。エントロピーが増大し続けるため、幾何学的な「淘汰」の対象となる。
\begin{equation} \frac{d\mathcal{W}}{d\tau} = \int_{M} 2\tau \left( \ln |\chi(s)| \right)^2 e^{-\Phi} dV > 0 \end{equation}

(4). 自己参照特異点の排除
　関数等式 $\zeta(s)=\chi(s)\zeta(1-s)$ が臨界領域 $0 < \operatorname{Re}(s) < 1$ において幾何学的に成立するための必要条件は、変換係数 $\chi(s)=2^s\pi^{s-1}\sin\left(\frac{\pi s}{2}\right)\Gamma(1-s)$ が、当該領域で解析的（holomorphic）かつ一価（Single-valued）であること、すなわち $\Gamma(1-s)\in\mathcal{O}(D)$ が満たされ、鏡像領域との循環連続性が保たれていることである。

$\mathcal{O}$: 正則関数 (Holomorphic Function)
D: 臨界帯 (Critical Strip)

自己参照特異点においては、構造変換係数が $\chi(s)=F(s,\zeta(s),\zeta(1-s),\chi(s))$ という自己依存性を持つ。この場合、$\chi(s)$ は外部変数のみによって決定される滑らかな関数ではなくなり、局所的な不連続性や分岐を含むため $\chi(s)\notin\mathcal{O}(D)$ となり解析的ではなくなる。したがって、滑らかな接続を前提とする関数等式は恒等式として成立せず、
\begin{equation} \Gamma(1-s)\chi(s)\notin\mathcal{O}(D) \end{equation}
となる。ゆえに、自己参照特異点は鏡像領域との循環連続性を満たさず、リッチフローモデルによる幾何学的淘汰の対象となる。

7. ゼロ無限算と極限の定義 (Definition of Zero-Infinity Arithmetic and Limits)

(1). ゼロ無限算の定義
ゼロ無限算（$1/\infty = 0$, $0 \times \infty = 1$）は、結節点における発散無限と循環無限の動的平衡状態として定義される。
\begin{equation} \Large \{ \boldsymbol{\infty}_{\text{div}} \rightleftharpoons \boldsymbol{\infty}_{\text{circ}} \} \equiv \{0 \cdot \infty\} = 1 \end{equation}
ゼロとは循環無限（$\boldsymbol{\infty}_{\text{circ}}$）であり、2進数においては、$0 \equiv 2^{-\infty}$ が厳密に成立する。$2^{-\infty}$ は極限値ではなく、循環無限（$\boldsymbol{\infty}_{\text{circ}}$）が占有する階層構造（grade structure） $2^n$ 階層の最上位を表す記号である。すなわち、$0$ は数値ではなく、循環無限（$\boldsymbol{\infty}_{\text{circ}}$）の階層と $\infty$ フロー構造の省略記号として定義される。発散無限 $\boldsymbol{\infty}_{\text{div}}$ と循環無限（$\boldsymbol{\infty}_{\text{circ}}$）は符号反転を通じた鏡像対応関係にあり階層的等価構造（Equivalent Structure）$2^{-\infty} \equiv 2^\infty$ の対を成す。同一グレードで他の要素を含まない場合、ゼロ除算は階層・構造の等価性により計算可能であり、$2^n$ においては、 $n$ が対の最上位階層であるため、鏡像対称性（mirror symmetry）より必然的に可逆である。なお、ゼロ点は $\infty$ フローにより内部構造（みえない球）に実数を格納する。したがって、$0 \cdot \infty$ グレードの峻別 (Strict Distinction) が推奨される。一般数理においては、ゼロ除算の問題だけではなく、$0 \cdot \infty$ を階層・構造として扱う $0 \cdot \infty$ 拡張が本質的に要求される。
\begin{equation} 0^0 = 0 \cdot 0^{-1} = 0 \cdot 2^\infty = 2^{-\infty} \cdot 2^\infty = 2^0 = 1 \end{equation}
\begin{equation} 2^{-\infty} \cdot 2^{\infty + 2} = 2^2 = 4 \iff 4 × 2^{-\infty} = 2^{-\infty + 2} = 0 \end{equation}
\begin{equation} n^\infty \cdot n^{-\infty} = 1 \quad (n \in \{k \in \mathbb{R} \mid k > 1\} \cup \{\infty\}) \end{equation}

(2). 空間と時間の定義
素数と合成数の定義: テオドロスの螺旋より素数と合成数を定義する。あるルート $\sqrt{\lambda} \quad (\lambda \in \{n \in \mathbb{Z} \mid n \ge 1\})$ を始点とするとき、$\lambda$ は その倍数系列の起源、$\sqrt{1}$ 始点 $(\sqrt{1}, \sqrt{2}, \sqrt{3} \dots)$ が正の整数、$\sqrt{2}$ 始点 $(\sqrt{2}, \sqrt{4}, \sqrt{6} \dots)$ が2の倍数の起源である。

素数の定義: 新波形 (New Waveform)
テオドロスの螺旋において、あるルート $\sqrt{p} \quad (p \in \{n \in \mathbb{Z} \mid n \ge 2\})$ が、他のいかなる $\sqrt{a}, \sqrt{b}$ の積でも表せない時、その $p$ を「素数（Prime Origin）」と定義する。
\begin{equation} \sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{11} \dots \end{equation}

合成数の定義: 波干渉 (Wave Interference)
テオドロスの螺旋において、あるルート $\sqrt{c} \quad (c \in \{n \in \mathbb{Z} \mid n \ge 2\})$ が、素数波形の積として分解できるとき、その $c$ を「合成数（Composite Numbers）」と定義する。
\begin{equation} \sqrt{c} = \sqrt{p_1} \times \sqrt{p_2} \times \dots \end{equation}

基底スケール変換公式 (Relativity of Scale): 基底 A が $A = B^k$ （例：$8 = 2^3$）であるとき、構造的同値性は、以下の変換を通じて異なるスケール間でも維持される。
\begin{equation} A^{(a \infty + b)} \iff B^{(k\cdot a \infty + k \cdot b)} \quad ((a \in \{n \in \mathbb{R} \mid n > 1\} \cup \{\infty\}) \wedge b \in \mathbb{R}) \end{equation}
世界構造は、素数基底と円周基底によって表され、次のように想定する。なお、本稿では、無限積はゼータ関数正則化 (Zeta Function Regularization) により解釈する。したがって、記号 $\stackrel{\mathrm{reg}}{=}$ は正則化手法によって導かれる等号を意味するものとする。
\begin{equation} \prod_{n=1}^{\infty} \sqrt{n} \stackrel{\mathrm{reg}}{=} e^{-\frac{1}{2}\zeta'(0)} = e^{-\frac{1}{2}\left( -\frac{1}{2}\log(2\pi) \right)} = \sqrt[4]{2\pi} \end{equation}
素数は自身を起源とする合成数系列を統括するため、その支配領域に応じた階層的な無限グレード ($n_p \infty$) による動的な無限量の調整によって、素数積は自然数積の総体と等価になり、円周基底との解析的な同一性が導かれる。なお、素数ゼータ関数 $P(s)=\sum p^{-s}$ は、オイラー積表示に基づく $\zeta(s)$ との解析的な等価性を前提とする。
\begin{equation} n_2 > n_3 > n_5 > \dots > n_p \quad (\text{Smaller Prime} \implies \text{Higher Grade}) \end{equation}
\begin{equation} \prod_{p} \sqrt{p^{(n_p \infty)}} \equiv \prod_{n=1}^\infty \sqrt{n} \stackrel{\mathrm{reg}}{=} \sqrt[4]{2\pi} \end{equation}
\begin{equation} \text{Universe} = \underbrace{\left( \prod_{p} p^{(n_p \infty + k_p)} \right)}_{\text{素数基底：発散}\infty} \times \underbrace{\left( \sqrt[4]{2\pi} \right)^{(N \infty + \alpha)}}_{\text{円周基底：循環}\infty} \stackrel{\mathrm{reg}}{=} \left( \sqrt[4]{2\pi} \right)^{{ \sum (n_p \infty + k_p) } + { N \infty + \alpha }} \end{equation}
\begin{equation} \left( \sum n_p \infty + N \infty \longrightarrow 0 \right) \bigwedge \left( \sum k_p + \alpha \longrightarrow 0 \right) \implies \text{Universe} = \left( \sqrt[4]{2\pi} \right)^{0} = 1 \end{equation}

統一理論構造と定数定義 (Structure of Unified Theory): 世界構造は、複素平面上における「空間の拡張（素数）」と「時間の回転（円周）」の鏡像対称性によって定義される。
\begin{equation} \underbrace{\prod_{p} \sqrt{p}}_{\text{空間（素数次元）}} \equiv \underbrace{\sqrt[4]{2\pi}}_{\text{時間（円周次元）}} \iff \frac{\text{空間（素数次元）}}{\text{時間（円周次元）}} = 1 \end{equation}
\begin{equation} \begin{split} &\mathbf{B} = \sqrt[4]{2} \cdot \sqrt{\Gamma\left(\frac{1}{2}\right)} = \sqrt[4]{2 \int_{0}^{\infty} e^{i \cdot 0} \, e^{-t} t^{-1/2} dt} = \sqrt[4]{2\pi} \\ \implies &\mathbf{B}^2 = \int_{-\infty}^{\infty} e^{-\frac{x^2}{2}} dx = {e^{-i\frac{\pi}{4}}} \int_{-\infty}^{\infty} e^{i\frac{x^2}{2}} dx = \sqrt{2\pi} \\ \implies &\mathbf{B}^4 = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-\frac{x^2+y^2}{2}} dx dy = {\left[ \int_{0}^{\infty} e^{-\frac{r^2}{2}} r \, dr \right]} {\left[ \int_{0}^{2\pi} e^{i \cdot 0} \, d\theta \right]} = 2\pi \end{split} \end{equation}
対称性の破れとは循環結晶の付与である。$\vec{\Phi}$ による循環結晶は質量形成である。
\begin{equation} \begin{split} (\sqrt[n]{1})^n &\xrightarrow{\text{Information (Manifestation) Symmetry Breaking}} \left( 1 + \frac{2\pi}{n} \right)^n \left( 1 + \frac{2\pi}{n} \right)^{-n} \\ &\xrightarrow{\text{Space Symmetry Breaking}} \left( 1 + \frac{i2\pi}{n} \right)^n \left( 1 + \frac{i2\pi}{n} \right)^{-n} (= e^{i2\pi} e^{-i2\pi}) \\ &\xrightarrow{\text{Time Symmetry Breaking}} \prod_{p} \left( \frac{1}{1 - p^{-s}} \right) \frac{\prod p}{\sqrt[4]{2\pi} \cdot \text{S}_{\text{symmetry}}} \\ &\xrightarrow{\text{Speed Symmetry Breaking}(\vec{V}{\text{: Vector}})} \prod_{p} \left( \frac{1}{1 - p^{-s}} \right) \left[ \frac{\prod p}{\sqrt[4]{2\pi} \cdot \text{S}_{\text{symmetry}}} \right] \vec{\Phi} \end{split} \end{equation}

(3). $\epsilon$ - $\delta$ 論法の役割の終焉と極限の厳密定義

定義　極限の定義: 限りなく近づき続ける。

極限の再定義（永続フロー）: 極限とは、一点への「収束・停止」ではなく、限りなく構造が更新され続ける「永続フロー（Perpetual Flow）」として再定義されなければならない。円周率を始めとする無理数は、$\forall n \, \exists n' \quad (0 < n < n')$ の要件を厳密に満たすが、これは計算が完結しない「実数永続フロー」である。つまり、$\forall n \, \exists n'$ は永続の要件であって収束（停止）の要件ではなく、この意味において、有限の微小な誤差（$\epsilon$）で計算の停止を擬似的に演出する $\epsilon$ - $\delta$ 論法は、構造記述として厳密に破綻している。

ゼロと無限の階層的峻別: 本理論において「ゼロは循環無限」であり、その本質は計算不可世界のフロー概念（無限フロー）に属する。したがって、ゼロと他の有理数との間にある収束整合性は、異なる階層を混同したカテゴリー・エラーであり、数学的意味を成さない。例えば、「素数砂漠が無限に続く」という結論が、そのまま「素数が無限に存在する」という結論を代替できないのと同様に、無限の広がりはその内部構造のフローによってのみ定義される。

絶対収束と永続性の両立: 上位階層から下位無限へと限りなく近づく過程は、数値的には「絶対収束」の形式を採るが、それは構造の「完了」を意味しない。最下位グレードを除く無限に限りなく近づき続けることによって、その下位無限になるのであり、数学が扱うべきは、収束という「結果（停止）」ではなく、フローという「構造の持続（永続）」である。

(4). ゼロ無限算と有限形成プロセス：構造的スケールの抽出}

定義　[有限値の定義] 無限基底・指数項の鏡像対称性及び有限基底の鏡像対称性がもたらす数値化プロセス (Numerical Realization Process)。

極限操作の本質は、対象が特定の領域に「到達」することではなく、その領域へ限りなく近づき続けるプロセスを記述することにある。ゼロ・無限の真の構造性の定義には、このプロセスの中に保存される「構造の比」を同定する手続きが不可欠である。

観測方程式 (Observation Equation): 異なるポテンシャル（指数 $a(s),\,b(s)$）を持つ構造間の接続を、変換係数 $\mathcal{T}$ を用いて次のように記述する。ここで「基底」$n \, (1 < n < \infty \, \cup \, n \equiv \infty)$ とは項の底（base）を指し、基底をそれぞれ固定定数 $n_A,n_B$ とする。
\begin{equation} T_A(N;s)= n_A^{-\phi(N)+a(s)},\quad T_B(N;s)=n_B^{-\phi(N)+b(s)} \end{equation}
このとき、変換係数 $\mathcal{T}$ は両構造の比の極限として現れる。$N \equiv \infty$ のとき、$N$ と $\infty$ は構造的に等価である。
\begin{equation} \mathcal{T}(N;s) = \lim_{N\to\infty}\frac{T_A(N;s)}{T_B(N;s)} = \lim_{N\to\infty}\Big(\frac{n_A}{n_B}\Big)^{-\phi(N)} n_A^{a(s)-b(s)} \end{equation}
この式から明らかなように、有限比 $\mathcal{T}$ を得るためには $n_A=n_B$（同一の固定基底）かつ $n < \infty$ （有限値）であれば発散因子は恒等的に打ち消され、$\mathcal{T}(s) = n^{a(s)-b(s)}\quad(n=n_A=n_B)$ が成り立つ。
\begin{equation} T_A(N;3) = 2^{-\phi(N)+4}, \quad T_B(N;3) = 2^{-\phi(N)+1} \end{equation}
\begin{equation} \mathcal{T}(N;3) = \lim_{N\to\infty} \frac{2^{-\phi(N)+4}}{2^{-\phi(N)+1}} = 2^{4-1} = 8 \end{equation}

構造的等価関係 (Structural Equivalence): 2つの基底 $T_A, T_B$ が $\phi(N) \to \infty$ において同種の構造（同じ底の性質）を持つことを、以下の同値関係 $\sim$ で定義する。
\begin{equation} T_A \sim T_B \iff \lim_{N \to \infty} \frac{T_A(N)}{T_B(N)} = C, \quad (0 < |C| < \infty) \end{equation}
この条件を満たすとき、両者は「同一の構造クラス」に属する。

整合的スケール因子 $\sigma(s)$: 基底の等価性（$n_A = n_B$）が担保され、かつ $n < \infty$ であるとき、観測される比 $\mathcal{T}$ は構造（指数 $a, b$）のみから一意に導かれる。つまり、等式を整合させる真の手段は、構造全体を統括する乗法的スケーリング ($\mathcal{T}$) へと一元化されることであり、これにより構造の同定プロセスにおける厳密性が担保される。
\begin{equation} \mathcal{T} \cdot T_B = T_A \implies \sigma(s) = \mathcal{T} \end{equation}
ここで $\sigma(s)$ は、構造の同値性を破壊せずに（基底 $n$ を変えずに）等式を整合させる唯一のスケール因子であり、変換係数 $\mathcal{T}$ そのものである。

(5). 現代数学の論理破綻の解消
以上により、循環小数や無理数が計算不可世界 ($\infty$) に到達しなければ厳密に収束しない永続フローであるのに対し計算可世界において計算完了（収束）とする極限概念の論理破綻が解消された。また、無限拡張は、ゼロ除算を構造的必然として内包し、無限への代入操作は、ゼロへの代入操作が直ちに可能であることと整合する。無限フローという「実体」から乖離した現代数学（その姿勢）は、むしろ構造の正当性を問われる立場にあり、本論が提示するフローの等価性こそが数値の真の起源 (origin) を明らかにするものである。

8. 鏡像対称性と有限化原理によるリーマン予想の構造的証明 (Structural Proof of the Riemann Hypothesis via Mirror Symmetry and Finitization Principle)

(1). 宇宙的鏡像としてのゼータ関数
本証明は、リーマン・ゼータ関数 $\zeta(s)$ の非自明な零点がすべて臨界線 $\operatorname{Re}(s)=1/2$ 上に存在することを、発散場（Divergence Field） と 循環場（Circulation Field） の 鏡像対称性（Mirror Symmetry） に基づく構造的均衡として確立するものである。本証明の核心は、関数等式が定める写像 $s \leftrightarrow 1-s$ が、トポロジー的に同相な二つの無限構造（発散 $\infty_{\text{div}}$ と 循環 $\infty_{\text{circ}}$）を結ぶ鏡像操作であり、その対称性がエネルギー保存的に成立する唯一の座標が $\operatorname{Re}(s)=1/2$ であるという幾何学的事実にある。

(2). 場の定義と構造的重み
発散場 (Divergence Field): 領域 $1 < \operatorname{Re}(s)$ は、正の整数構造に由来する「無限大への発散ポテンシャル」が支配的な場である。特異点 $s=1$ を起点とし、その構造的最小単位の寄与により、正の構造的重み $\mathbf{F}_+ = +1/2$ を持つ。
循環場 (Circulation Field): 領域 $\operatorname{Re}(s) < 0$ は、解析接続によって負の整数サイクル（循環構造）へと写像された場である。発散の鏡像である $s=0$ を境界定数とし、解析接続値 $\zeta(0) = -1/2$ により、負の構造的重み $\mathbf{F}_- = -1/2$ を持つ。

(3). 関数等式と鏡像対称性の三段階要請
ゼータ関数の全平面における構造は、関数等式 $\zeta(s) = \chi(s)\zeta(1-s)$ によって統制される。この鏡像対称性は、以下の三段階の構造的要請によって成立する。

第1要請（半径一致）: 鏡像対称性は第一に「リーマン次元円」の半径一致を要請する。基準円 $|S^s| = 2^s$ と鏡像円 $|S^{1-s}| = 2^{1-s}$ の半径差 $\Delta r$ が消失する条件は、実部のみの条件から導かれ、$\operatorname{Re}(s) = 1/2$ を唯一の解として与える。
\begin{equation}|\chi(s)| = 1 \iff |2^s| = |2^{1-s}| \iff \operatorname{Re}(s) = \frac{1}{2} \end{equation}

第2要請（円としての複素拡張）: 実部が $1/2$ に固定された後、リーマン次元円は虚部 $it$ による螺旋拡張を受け、臨界線 $\operatorname{Re}(s)=1/2$ 上に全ての位相を載せる。複素平面上の時間は回転として作用し、この回転位相が結節点（Nexus）の周囲を周回するエネルギーの渦となる。

第3要請（リーマン次元点 = $\Gamma$）: $\Gamma$ 関数（鏡像循環係数）は、複素平面上の点スピン循環∞（リーマン次元点）を、既に確定したリーマン次元円上に一貫して解析接続する。この操作により、発散∞と循環∞の局所的均衡点（非自明ゼロ点）は、構造変換係数の絶対値が $1$ となる経路上に厳密に定められる。

(4). 有限化原理と物理的メカニズム
上記の幾何学的要請が、なぜ臨界帯において厳格に適用されるのか。その物理的根拠を以下に示す。

ディリクレ級数によるエネルギー供給と一般化されたエントロピー: ディリクレ級数が収束する領域 $\operatorname{Re}(s)>1$ では、無限級数 $\sum n^{-s}$ が常に正味の「外部エネルギー供給」として働き、系にスカラー束を注入し続けている。この外部供給が、構造の歪みによって生じるエントロピー増大を強制的に相殺（Compensate）するため、系は崩壊せず数値を維持できる。しかし、臨界帯（$0<\operatorname{Re}(s)<1$）ではディリクレ級数が不収束となるため、外部供給は完全に停止する。この孤立系において、リッチフローにおけるエントロピー増大則 $\frac{d\mathcal{W}}{d\tau} \ge 0$ は、自己参照特異点に限らず、「あらゆる幾何学的非対称性（半径の不一致、曲率の歪み）」 に対して作用する数式的な強制力である。したがって、もし構造内部に無限の発散要因（スケール差）が生じた場合、ガンマ関数にはそれを抑え込む力がないことが数学的に確定しており、$0 < s < 1$ では、$\chi(s)=2^{s}\pi^{s-1}\sin(\frac{\pi s}{2})\Gamma(1-s) \neq 0$ かつ有限である。

ガンマ関数の役割（有限領域における調整の限界）: 臨界帯 $0 < s < 1$ において、ガンマ関数 $\Gamma(s)$ は極もゼロ点も持たず、滑らかな「有限の値（複素係数）」のみを提供する。これは極めて重要な事実を示唆する。すなわち、この領域におけるガンマ関数は、 $\zeta(s)$ と $\zeta(1-s)$ に対して常に乗法的に作用し、構造の不整合を強制的にゼロや無限大へ封じ込める「無限の調整力」を持たず、単なる有限の回転・伸縮調整しか行えない。したがって、もし構造内部に無限の発散要因（スケール差）が生じた場合、ガンマ関数にはそれを抑え込む力がないことが数学的に確定している。

$|0|$ の定義：スケール比較のための構造単位 通常の演算において $0/0$ は不定形となり計算不可能である。本証明では、基準と鏡像の幾何学的な「スケール差」を厳密に比較・検証するために、基底 $n$ ($n > 1$) を用いて、ゼロ点の実体を以下の極限形式として定義する。
\begin{equation} |0| \equiv n^{-\infty} \end{equation}
この定義により、数値的な $0$ の除算ではなく、極限項同士の「比の演算」が可能となる。これは、隠れたスケール係数（$\text{scale}$）を数式上に顕在化させ、対称性の破れを定量的に判定するために用意された検証用の構造単位である。

(5). 加法的な調整の禁止と乗法的閉包性

関数等式による構造の定義 : リーマンの完備ゼータ関数 $\xi(s)$ の関数等式は以下の通りである。
\begin{equation} \pi^{-s/2} \Gamma(s/2) \zeta(s) = \pi^{-(1-s)/2} \Gamma((1-s)/2) \zeta(1-s) \end{equation}
　この等式は、複素平面全体において $\zeta(s)$ と $\zeta(1-s)$ が、ある変換係数を介して「乗法的に（Multiplicatively）」結びついていることを示している。すなわち、両者の関係は常に「比（Ratio）」によって記述される。

クリティカル・ストリップ領域 ($0 < Re(s) < 1$) におけるゼータ関数の振る舞いは、ディリクレ・エータ関数（交代級数）によって記述される。
\begin{equation} \zeta(s) = \frac{1}{1-2^{1-s}} \eta(s) = \frac{1}{1-2^{1-s}} \sum_{n=1}^{\infty} (-1)^{n-1} n^{-s} \end{equation}
ここで重要な事実は、収束のための符号交代項 $(-1)^{n-1}$ や大域的係数 $(1-2^{1-s})^{-1}$ が付与されたとしても、鏡像変換 $\mathcal{T}$ は、指数 $s$ の反転のみの作用素であり、級数を構成する構造の要素は依然として $n^{-s}$ であるという点である。
\begin{equation} \mathcal{T}: n^{-s} \longleftrightarrow n^{-(1-s)} \end{equation}

未知の基底による構造比較 : ここで重要となるのは、$0 < s < 1$ かつ $\zeta(s) = \zeta(1-s) = 0$ の時では、「足し算・引き算」による誤差調整の余地が存在しないことである。通常、数値のズレを補正する場合、以下のような加法的な操作（指数への定数加算など）が想定されるかもしれない。
\begin{equation} \text{Example: }4 = 2^{-\infty + \infty + 2} \quad (\text{指数への加算による調整}) \end{equation}
$\zeta(s) = \zeta(1-s) = 0$ の時、左辺と右辺の基底（Base）が同一であるかは未確定であるため、それぞれ別の未知数 $N_A, N_B$ と置く。観測される変換係数 $\chi(s)$ より、構造間の等号を定義する。
\begin{equation} N_A^{-\infty + a} = \chi(s) \cdot N_B^{-\infty + b} \end{equation}
ここで、仮に「基底が同一である場合（$N_A = N_B = n$）」、係数 $\chi(s)$ と基底 $n$ の間には以下の関係が成立しなければならない。
\begin{equation} \frac{n^{-\infty + a}}{n^{-\infty + b}} = n^{a-b} = \chi(s) \end{equation}

次に、「基底が同一ではない場合（$N_A = n, N_B = n \cdot \text{scale}$）」、係数 $\chi(s)$ と基底 $n$ 及び $n \cdot \text{scale}$ の間には以下の関係が成立する。
\begin{equation} \frac{n^{-\infty + a}}{n^{-\infty + b} \cdot \text{scale}^{-\infty + b}} = n^{a-b} \cdot \text{scale}^{\infty - b} = \chi(s) \end{equation}
リーマン予想が真であるならば、$\frac{n^{-\infty + a}}{n^{-\infty + b}} = \chi(s)$ は $a = b$ のみ、偽であれば、$a \neq b$ でも成立する。$P=NP$（構造的等価）は、世界構造の等価性（鏡像対称性）を基盤とし、その成立は真であれば、「一つの真理と他全ての矛盾」を表し、偽であれば、「一つの矛盾と他全ての真理」を表す。したがって、その無効性は後者の論理に対応するため、「逆背理法」による証明が必要となる。本論において構造的矛盾が存在しないという事実は、逆説的にリーマン予想が偽である可能性を示唆している。

局所展開による関数等式 $\chi(s)$ の極限値の導出 : 点$s \to s_0$ における $\zeta(s)$ および $\zeta(1-s)$ を、それぞれの零点（または極）の位数 $m, n$ を用いて局所展開（テイラー展開の主要項）する。

1. 局所的な漸近展開
   点 $s \to s_0$ における値を、誤差項 $r(s) = o((s-s_0)^k)$ を保持したまま分数形式に代入。
   \begin{equation} \frac{\zeta(s)}{\zeta(1-s)} = \frac{c_A(s-s_0)^m + r_A(s)}{c_B(s-s_0)^n + r_B(s)} \end{equation}

2. 共通因数の括り出し
   分母・分子から、それぞれの主要項の次数である $(s-s_0)^m$ および $(s-s_0)^n$ を括り出す。
   \begin{equation} \frac{\zeta(s)}{\zeta(1-s)} = \frac{(s-s_0)^m \left( c_A + \dfrac{r_A(s)}{(s-s_0)^m} \right)}{(s-s_0)^n \left( c_B + \dfrac{r_B(s)}{(s-s_0)^n} \right)} \end{equation}
   ここで、$o$ の定義 $r(s) = o((s-s_0)^k)$ より、以下の極限が成立する。
   \begin{equation} \lim_{s \to s_0} \frac{r_A(s)}{(s-s_0)^m} = 0, \quad \lim_{s \to s_0} \frac{r_B(s)}{(s-s_0)^n} = 0 \end{equation}

3. $m=n$ の場合の漸近挙動
   特に位数が一致する場合（$m=n$）、$(s-s_0)^{m-n} = 1$ となり、式は以下のように整理される。
   $$\frac{\zeta(s)}{\zeta(1-s)} = \frac{c_A + o(1)}{c_B + o(1)} = \frac{c_A}{c_B} \left( 1 + \frac{o(1)}{c_A} \right) \left( 1 + \frac{o(1)}{c_B} \right)^{-1}$$
   　これを $s \to s_0$ の周りで展開（幾何級数展開）すると：
   \begin{equation} \frac{\zeta(s)}{\zeta(1-s)} = \frac{c_A}{c_B} + \underbrace{\left[ \frac{r_A(s)}{c_B(s-s_0)^n} - \frac{c_A r_B(s)}{c_B^2(s-s_0)^n} + \dots \right]}_{o(1)} \end{equation}
   これにより、誤差項は $s \to s_0$ において消失し、定数項 $\frac{c_A}{c_B}$ が抽出される。

4. 最終的な定式化
   \begin{equation} \begin{aligned} \chi(s_0) &= \lim_{s \to s_0} \frac{c_A(s-s_0)^m + r_A(s)}{c_B(s-s_0)^n + r_B(s)} = \frac{c_A}{c_B} \cdot \lim_{s \to s_0} (s-s_0)^{m-n} \\ &= \begin{cases} 0 & (m > n) \\ \dfrac{\zeta^{(m)}(s_0)}{(-1)^m \zeta^{(m)}(1-s_0)} & (m = n) \\ \infty & (m < n) \end{cases} \end{aligned} \end{equation}

(6). 結論：構造的均衡と唯一性（リーマン予想を真とする場合）
第1要請の不履行による対称性の破綻（自明な前提）: 臨界帯において $\operatorname{Re}(s) \neq 1/2$ である場合、基準円と鏡像円の半径が一致しない時点で、幾何学的な「スケール差（Scale Difference）」が発生しており、完全な鏡像対称性が破れていることは自明である。
\begin{equation} |2^s| \neq |2^{1-s}| \iff |\chi(s)| \neq 1 \end{equation}

残存要件による比の検証（$0/0=1$ の成否）: 対称性が破れた（$|\chi(s)| \neq 1$）状態で、第2・第3要請が機能したとしても、$|0|$ 同士の構造比が $1:1$ に収束し、均衡点（Nexus）を形成できるかが焦点となる。しかし、(5)で定義した有限指数項 $a, b$ を含めて検証しても、スケール差（スケール比 $n \neq 1$）が存在する以上、その比は以下のように発散する。
\begin{equation} \frac{|0|{\text{base}}}{|0|{\text{mirror}}} = \frac{n^{-\infty+a}}{(n \cdot \text{scale})^{-\infty+b}} = n^{a-b} \cdot \text{scale}^{\infty-b} \implies \infty \quad (|0|_{\text{base}} < |0|_{\text{mirror}}) \end{equation}

エントロピー増大による幾何学的淘汰: 上記の結果、系には $\text{scale}^{\infty}$ という無限のエントロピー増大（エネルギー不均衡）が発生する。これに対し、系を繋ぐ変換係数 $\chi(s)$ は「有限の重み」しか持たない。有限の力しかない $\chi(s)$ では、この無限大の幾何学的乖離を強制的に $1$ へと補正することは不可能である。したがって、比が $1:1$ とならない全ての座標は、リッチフローの単調増大則による淘汰圧に耐えられず、構造として即座に崩壊する。
よって、非自明なゼロ点が永続的に存立し得る唯一の条件は、最初の段階でスケール差が存在せず（$\text{scale}=1$）、かつ有限指数も一致する ($a=b$) ことで、鏡像対称性構造として
\begin{equation} \frac{n^{-\infty+a}}{n^{-\infty+b}} = 1 \end{equation}
という完全均衡が成立する $\operatorname{Re}(s)=1/2$ に厳密に限られる。

9. おわりに (Final Remarks)

リーマン予想は、ゼロ点を解析接続の「構造的均衡点」として再定義することで解決される。数値 $1/2$ は恣意的なものではなく、直線的な発散（正）と円環的な反復（負）の間のトポロジカルな変換を釣り合わせるために必要な基本定数である。この数学的「発散・循環構造」は、物理的宇宙における世界構造式へと帰結する。