競技数学解説

三角形の垂心について

垂心,初等幾何,競技数学典型

676

はじめに

　こんにちは！sta_kunです．

　今回は垂心の性質について紹介していきたいと思います．初学者にもわかりやすいように書いたつもりなのでぜひご一読ください！

　なお，この記事では図1のように点を定義します．

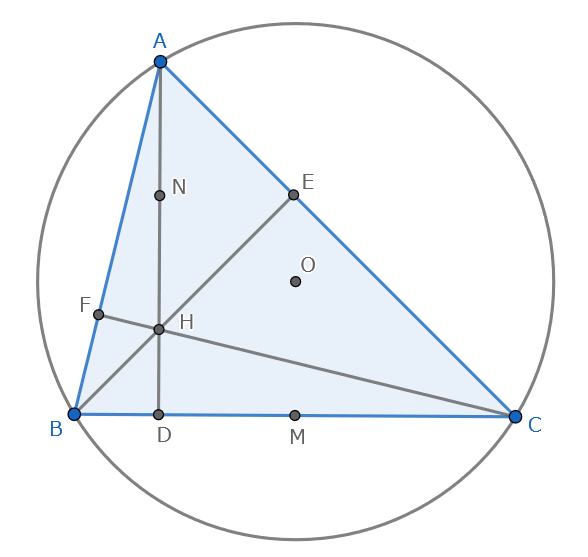
三角形$ABC$について，垂心を$H$，外心を$O$，$3$点$A,B,C$から対辺に下した垂線の足をそれぞれ$D,E,F$，線分$BC,AH$の中点をそれぞれ$M,N$とする．

垂心の基本構図

共円と相似

$4$点$A,E,H,F$は$N$を中心とする円周上にある．
$4$点$B,F,E,C$はMを中心とする円周上にある．
$\triangle ABD∽\triangle CHD$
$\triangle ABC∽\triangle AEF$

　証明は全て簡単な角度追跡から従うのでここでは省略させていただきます．

　次の構図はOMCなのでもよく見かける比較的有名なものです．

垂心の対称移動

　$H$を辺$BC$に関して対称移動させた点を$X$，$H$を点$M$に関して対称移動させた点を$Y$とすると，

$X$は$\triangle ABC$の外接円上にある．
$Y$は$\triangle ABC$の外接円上にあり，特に$AY$は外接円の直径である．

(1)$\angle BXC=\angle BHC=\angle BHD+\angle CHD=\angle ACB+\angle ABC=180\degree-\angle BAC $
　より示された．
(2)このとき四角形$BHCY$は平行四辺形．よって$\angle ABY=\angle ACY=90\degree$より示された．

定理2から，次の九点円の定理がわかります．

九点円の定理

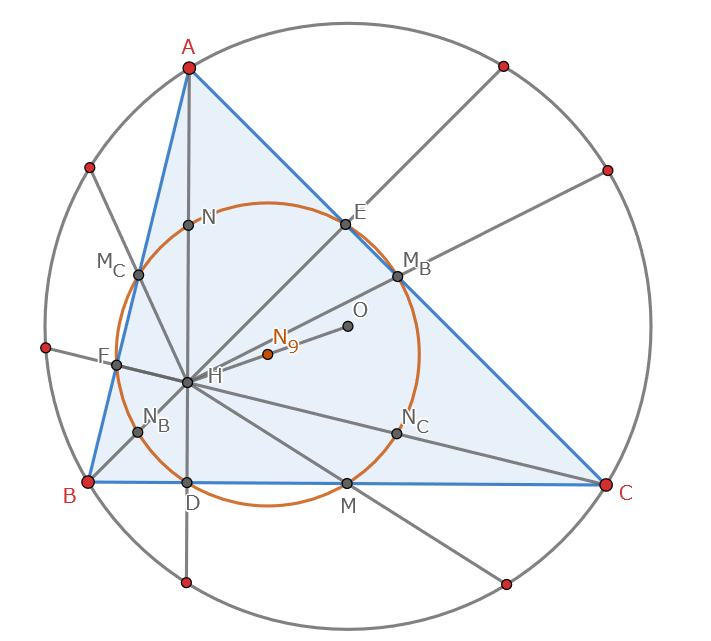
　線分$AC,AB,BH,CH$の中点を$M_B,M_C,N_B,N_C$とすると，$9$点$D,E,F,M,M_B,M_C,N,N_B,N_C$は同一円周上にある．特にこの円を九点円と呼ぶ．さらに，この円の中心$N_9$は線分$OH$の中点である．

　定理2より，図2の$9$つの赤点は外接円上にある．これらに$H$を中心とする$\dfrac{1}{2}$倍の相似拡大（半分に縮小するイメージ）を施すことで題意は従う．（円の中心も，$H$を中心に$O$が半分に縮小されるので$OH$の中点であることがわかる．）

この定理を使うと，以下の定理が示されます．

垂軸

　$EF$と$BC$の交点を$X$，$CA$と$DF$の交点を$Y$，$AB$と$DE$の交点を$Z$とすると，$3$点$X,Y,Z$は共線で，この直線を特に垂軸と呼ぶ．さらに，垂軸はオイラー線（後述）と直交する．

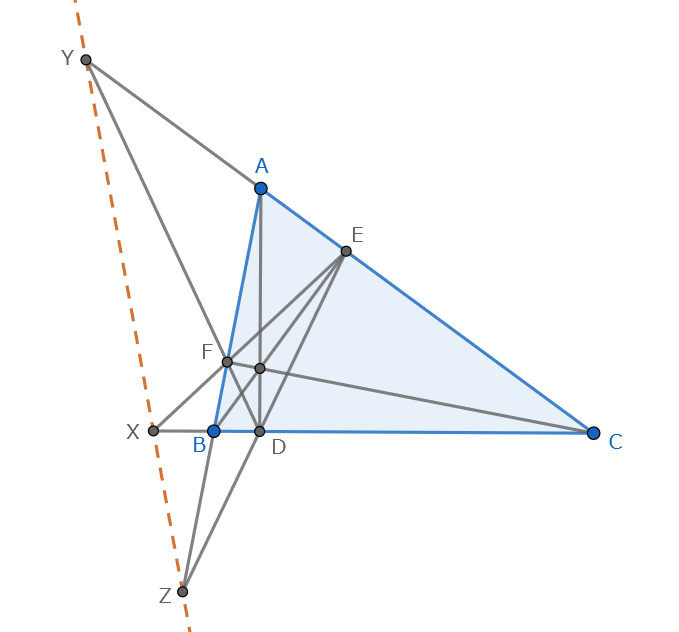
　円$BFEC$と外接円の根軸は直線$BC$，円$BFEC$と九点円の根軸は直線$EF$より，$X$は外接円と九点円の根軸上に位置する．同様に$Y,Z$も根軸上にあるので，示された．また，外接円の中心は$O$，九点円の中心$N_9$は$OH$上より，垂軸は直線$ON_9$すなわち直線$OH$と直交する．

次は，symmedianにも絡んでくる重要な性質です．

三接線補題

　$A$を通り$BC$に平行な直線，直線$ME$，直線$MF$は全て円$AEF$に接する．

　円$AEF$ の外心は$N$で，$AN\perp BC$から$A$を通り$BC$に平行な直線は円$AEF$に接する．また，$MB=ME$から$\angle MEB=\angle MBE=\angle HAE$より，接弦定理の逆から，直線$ME$は円$AEF$に接する．直線$MF$も同様．

定理5を使って以下の性質を示してみましょう．

類似中線(symmedian)

　円$ABC$の$B,C$それぞれにおける接線の交点を$X$とすれば，$\angle BAX=\angle CAM$が成り立つ．なお，このとき直線$AX$は三角形$ABC$の類似中線と呼ぶ．

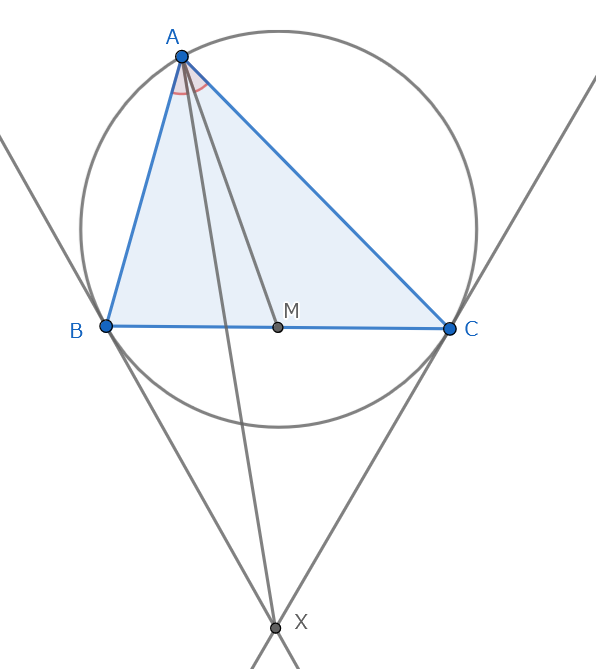
　定理5より，円$AEF$の$E,F$それぞれにおける接線の交点は$M$である．これと$\triangle AEF∽\triangle ABC$を合わせて，$\triangle AEM∽\triangle ABX$を得る．よって$\angle BAX=\angle CAM$である．

類似中線には他にもたくさんの性質があります．興味のある方はぜひ調べてみてください！

では，練習問題を解いてみましょう．（出典の書いていない問題は，一般的に知られているものか自作のものです．）

　問題1はJMO予選の問題です．セットとして解きたい場合は飛ばすことをお勧めします．　

JMO2021年予選7番

　三角形$ABC$の辺$BC$上に点$P,Q$があり，三角形$ACP$の垂心と三角形$ABQ$の垂心は一致している．$AB=10,AC=11,BP,5,CQ=6$のとき，辺$BC$の長さを求めよ．

ヒント

　定理2を思い出しましょう．

解答

　$A$から$BC$に下した垂線と$BC$，円$ABQ$の交点をそれぞれ$X,Y$とする．$x=PX,y=QX$とする．定理2より，$A,P,Y,C$は共円．よって，方べきの定理より，
$$ (5+x)y=AX\cdot XY=x(y+6)$$
三平方の定理より，
$$ AX^2=100-(x+5)^2=121-(y+6)^2$$
これを解いて，$x=5\sqrt{\dfrac{21}{11}}-5,y=6\sqrt{\dfrac{21}{11}}-6$．よって，$BC=\sqrt{231}$である．

sta_kun杯 p1

　鋭角三角形 $ABC$ があり，その垂心を $H$ とする．線分 $AH$ の中点を $P$，$CH$ と三角形 $ABC$ の外接円の交点（$\neq C$）を $Q$ とすると，円 $PQH$ は直線 $BH$ に接した．このとき，線分 $BC$ の中点を $M$ とすると $AB=AM$ であることを示せ．

ヒント

　条件より，$\triangle PQH∽\triangle ACB$がわかります．さらに，定理$2$から何がわかるでしょうか？

解答

　$B,C$から対辺に下した垂線の足をそれぞれ$E,F$とする．接弦定理より，
$$ \angle PQH=\angle PHE=\angle ACB$$
これと，$\angle ABC=\angle PHQ$，$HF=FQ$，$BM=MC$ と合わせて，($A,B,C,M$)と($P,H,Q,F$)は相似である．このとき，$P$が円$AFHE$の中心であることに留意して，$PF=PH$を得る．よって$AB=AM$で，題意は示された．

　$AH$と$EF$の交点を$P$とする．このとき，点$P$は三角形$NBC$の垂心であることを示せ．

ヒント

　角度追跡では難しそうです．方べきの定理で長さを追うことを考えましょう．また、Brocardの定理を用いれば瞬殺です．

解答

　$BC$に関して$H$と対称な点を$X$とすると，$\angle BXA=\angle BHD=\angle ACB=\angle AFE$より$4$点$P,F,B,X$は共円．このとき方べきの定理から
$$AP\cdot AX=AF\cdot AB=AH\cdot AD$$
また，
$$DP\cdot DN=(AD-AP)\cdot \dfrac{AX}{2}=\dfrac{AD}{2}\cdot (AX-AH)=AD\cdot DX=BD\cdot DC$$
より，$DP:DC=DB:DN$ がわかり，$\triangle BDN∽\triangle PDC$ より示された．

別解

　内接四角形$AEHF$に対しBrocardの定理を適用することでただちに従う．

HKA杯 p8

　$AB \lt AC$ である鋭角三角形 $ABC$ について，$BC$ の中点を $M$，$AM,BM,CM$ の中点をそれぞれ $N,X,Y$ とする．また，$M$ から $AC$ に下した垂線の足を $D$，$X$ を通り $DY$ に平行な直線と直線 $DN$ の交点を $P$，三角形 $PNX$ の外接円と $AB$ の交点のうち $A$ に近い方を $Q$，三角形 $PNX$ の外接円と $BC$ の $X$ でない交点が存在したので $R$ とする．ここで，三角形 $PNX$ の外接円と $DR$ の交点を $S$ とするとき，$3$ 点 $Q,S,M$ は同一直線上にあることを示せ．

ヒント

　九点円っぽい見た目をしていますね。aminoの補題も有効です．

解答

　三角形$AMC$の九点円と$BC$の交点のうち$B$に近い方を$R^{\prime}$とする．$R^{\prime}$は$A$から$BC$に下した垂線の足である．このとき，
$$ \angle NRX=\angle NPX=\angle 180\degree-\angle YDN=\angle NR^{\prime}X$$
から，$R$と$R^{\prime}$は一致する．すなわち，円$PNX$は三角形$ABM$の九点円である．
ここで，$AM\leqq BM$と仮定すると，$\angle ABM\leqq \angle BAM$，$\angle ACM\leqq \angle CAM$ より$\angle BAC$が鋭角とならず矛盾．よって$AM\gt BM$で，点$Q$は$AB$の中点である．このとき$QM\parallel AC$である．
ここで，円$PNX$と$AB$の交点（$\neq Q$）を$T$とする． $\angle ATM=\angle ARM=\angle ADM=90\degree$より$A,T,R,M,D$は共円で，
$$ \angle BAC=180\degree-\angle TRS=\angle TQS$$
より$AC\parallel QS$である．
$QM\parallel AC$と合わせて，$Q,S,M$は共線で，示された．

他の五心との関係

垂心と傍心の双対性

双対性

　$H$は三角形$DEF$の内心であり，$A,B,C$は三角形$DEF$の傍心である．

　$\angle FDH=\angle FBH=\angle FCE=\angle EDH$より$H$は三角形$DEF$の内心である．また，$\angle HFA=\angle HEA=90\degree$より$A$は三角形$DEF$の傍心．同様に$B,C$も傍心で，示された．

オイラー線

　三角形$ABC$の重心を$G$とすると，$O,G,H$は同一直線上にあり，さらに$OG:GH=1:2$である．なお，この直線をオイラー線と呼ぶ．

オイラー線にはたくさんの証明法があります．ここでは相似拡大を用いたものを紹介します．

　$BC,CA,AB$の中点をそれぞれ$M_A,M_B,M_C$とする．三角形$ABC$に$G$を中心とする$-\dfrac{1}{2}$倍の相似拡大を施すことで，三角形$ABC$は三角形$M_AM_BM_C$に移る．このとき，この三角形の垂心を考えると，各辺の垂直二等分線の交点となり$O$と一致する．つまり，この相似拡大によって$H$が$O$に移っており，題意は示される．

外心との関係

等角共役

　$\angle BAH=\angle CAO$が成り立つ．このような関係のことを等角共役と呼ぶ．

　$\angle CAO=90\degree-\dfrac{1}{2}\angle AOC=90\degree-\angle ABC=\angle BAH$より示された．

それでは，練習問題です．

$AH=6,BC=8$ のとき，$EF$を求めよ．

ヒント

　三角形$ABC$と三角形$AFE$の相似比がわかればいいと考えて…

解答

　定理8より，$OM=\dfrac{AH}{2}=3$．$MC=4$より$OC=5$．一方，三角形$AEF$の外接円の半径は $\dfrac{AH}{2}=3$．よって相似比は$5:3$で，$EF=\mathbf{\dfrac{24}{5}}$．

　$AH$と$EF$の交点を$P$，線分$EF$の中点を$Q$，$EF$と$BC$の交点を$R$とし，三角形$ABC$の外接円と$EF$の交点を$S,T$とするとき，以下を示せ．

$AO\perp EF$
$MQ\perp EF$
$AS=AT$
$4$点$C,Q,P,B$は同一円周上

(1)　解答

　定理9より，$\angle BAD=\angle CAO$．三角形$AEF$の外心は$N$より，三角形$AEF$にもう一度定理9を適用することで，三角形$AEF$の垂心が$AO$上ににあることがわかり，示された．

(2)　解答

　$AO$と円$ABC$の交点を$X$とする．定理2より$HM=MX$で，$AN=NH$と合わせて$AX\parallel NM$，すなわち$EF\perp MN$．$N$は三角形$AEF$の外心より，$NQ\perp EF$．以上より，$N,Q,M$は共線で，特に$MQ\perp EF$である．

(2)　別解

　$EF$は$N$を中心とする円$AEF$と$M$を中心とする円$BFEC$の根軸より，$MN\perp EF$．後は同様．

(3)　解答

　$ST\perp AO$から示された．

(3)　別解

　$A$を中心とする半径$\sqrt{AD\cdot AH}$の円で反転（後述）しても$S,T$は不変．よって$AS=AT=\sqrt{AD\cdot AH}$で，示された．

(4)　解答

　(2)より，$M,Q,P,D$は共円．円$ABC,BFEC,MQPD,MDFE$について方べきの定理より，
$$ QR\cdot PR=MR\cdot DR=ER\cdot FR=CR\cdot BR$$
から，示された．

反転

　ここでは，垂心の絡む反転について紹介したいと思います．
まず，以下のように点を新しく定義します．

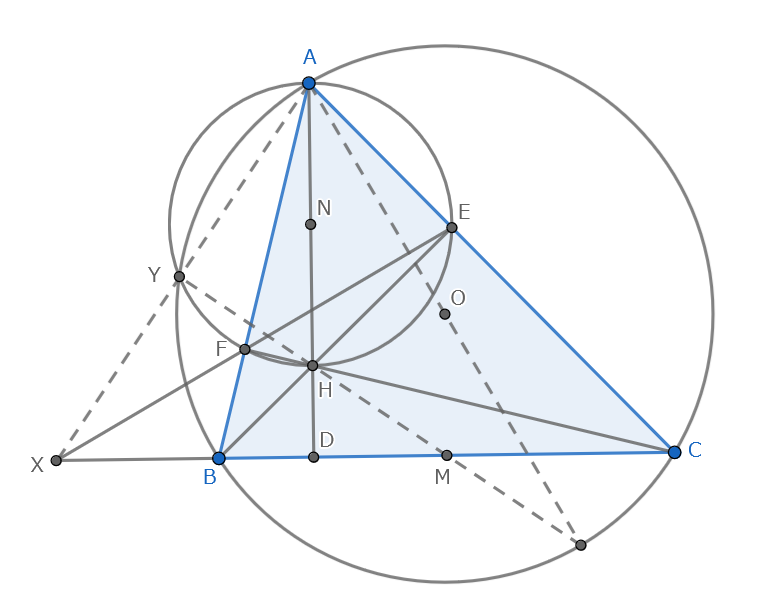
$BC$と$EF$の交点を$X$，円$ABC$と円$AEF$の交点を$Y$とする．

この図を少し観察すると，以下のことが分かります．

$A,Y,X$は共線
$M,H,Y$は共線

円$ABC,AEF,BFEC$の根心は$X$より，$A,Y,X$は共線．また，$A$を$O$に関して対称移動させた点を$Z$とすると，$\angle ZYA=90\degree$．$\angle AYH=90\degree$と合わせて，$Y,H,Z$の共線が従うが，定理2より$H,M,Z$は共線なので，$M,H,Y$は同一直線上にある．

点$Y$が内接四角形$BFEC$のミケル点となっていることを考えれば自然かと思います．

$A$中心の反転

　$B,F,H,D$の共円と$C,E,H,D$の共円から以下が従います．
$$ AF\cdot AB=AH\cdot AD=AE\cdot AC$$
このことから，次のことが分かります．

$A$中心の反転

　$A$を中心とする半径$\sqrt{AD\cdot AH}$の円で反転することで，$B$と$F$，$D$と$H$，$C$と$E$，($X$と$Y$) はそれぞれ移りあう．

　では，こちらの問題を解いてみましょう．

　JJMO2017本選5

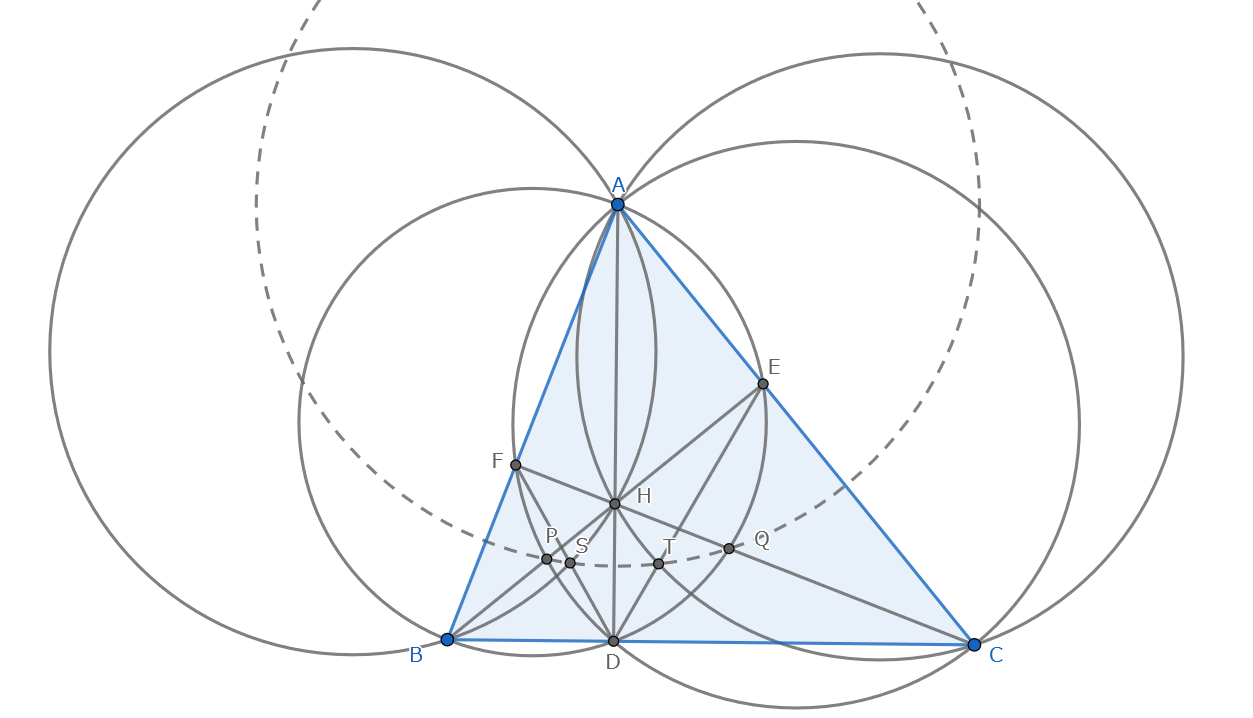
　鋭角三角形$ABC$があり，その垂心を$H$とする．3点$A,B,C$から対辺に下した垂線の足をそれぞれ$D,E,F$とする．三角形$ACD$の外接円と線分$BE$の交点を$P$，三角形$ABD$の外接円と線分$CF$の交点を$Q$とする．また、三角形$ABH$の外接円と線分$DF$の交点を$S$，三角形$ACH$の外接円と線分$DE$の交点を$T$とする．このとき，4点$P,Q,S,T$は同一円周上にあることを示せ．

解答

　$P,Q,S,T$はこの反転により不変である．よって，すべて基準円上にあり，示された．

$M$中心の反転

　線分$BC$を直径とする円で反転すると，九点円(定理3)が直線$EF$に移ります．このことから，以下のことがわかります．

$M$中心の反転

　線分$BC$を直径とする円で反転することで，$B,C,E,F$は不変で，$D$と$X$，$H$と$Y$はそれぞれ移りあう．

$H$と$Y$が移りあうことは内接四角形のミケル点の性質から従います．

　では，こちらの問題を解いてみましょう．

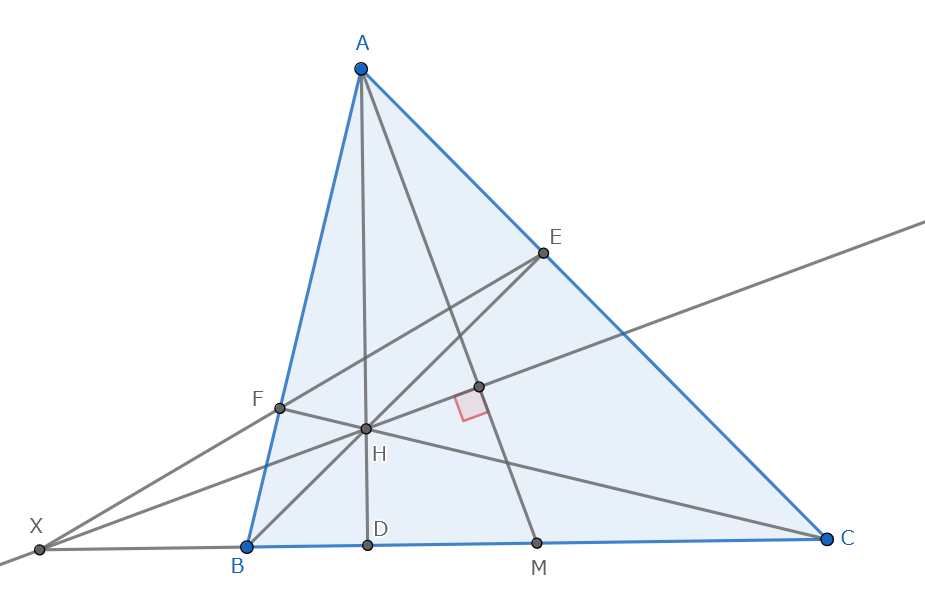
$XH\perp AM$を示せ．

解答

　$A$がこの反転によって移った先を$A^*$とすると，$\angle ADM=90\degree$より，$\angle XA^*M=90\degree$．また，$A^*$は円$BFM$と$CME$の交点なので，簡単な角度追跡より$A^*$は円$AEF$上にある，すなわち$\angle HA^*M=90\degree $がわかる．よって，$X,H,A^*$は同一直線上にあり，特に$XH\perp AM$である．

　最後に，反転を用いる練習問題を紹介します．少し難しいかもしれませんが，ぜひ考えてみてください．

HKA杯p11

　$AB \lt AC$ である鋭角三角形 $ABC$ があり，その垂心を $H$ とする．$3$ 点 $A,B,C$ からそれぞれ対辺に下した垂線の足をそれぞれ $D,E,F$ とする．また，$AH$ と $EF$ の交点を $G$，$BC$ の中点を $M$，$∠BAC$ の内角の二等分線と $BC$ との交点を $P$，$B$ を点 $D$ に関して対称移動させた点を $Q$ とする．ここで，$M$ を通り $AP$ に垂直な直線と，$P$ を通り $AM$ に垂直な直線は三角形 $ABC$ の外接円上で交わった．このとき，三角形 $AGE$ の外接円は直線 $QH$ に接することを示せ．