幾何コンテスト『T-DEMO Show 2025』の公式解説
初めましての方は初めまして、ご無沙汰している方はご無沙汰しております。
2025年12月11日から12月21日まで、
T-DEMO Show 2025
という、証明幾何のコンテストを開催させていただきました。告知からわずか5日での開催、誰にも気づかれない可能性まで危惧していましたが、有難いことに12名の参加者に恵まれました。有難い(再確認)。
本記事では、T-DEMO Show 2025の解説を紹介します。ここから真面目な文章が続くと予想されるため、気休めに「鋭角三角形$ABC$の3つの傍接円すべてについて、その円弧のちょうど半分を内部に含む円」を一発で描くGeoGebraコマンドをお届けしておきますETC。
Circle(Reflect(TriangleCenter(A,B,C,10),TriangleCenter(A,B,C,40)),(sqrt(4*(Radius(Incircle(A,B,C))+8*Radius(Circle(A,B,C)))^2-7*Perimeter(Polygon(A,B,C))^2)/4))
問題一覧
問題PDFが欲しい方は、 こちら からダウンロード可能です。
$AB=AC$をみたす二等辺三角形$ABC$において、その内接円を$i$とします。「直径が辺$BC$上にあり2辺$AB$, $AC$に接する半円」を$m$、「半円$m$の弧および2辺$AB$, $AC$に接する円」を$n$とするとき、円$n$の中心は円$i$の周上に存在することを示してください。
円$\Gamma$の周上に3点$A$, $B$, $C$をとり、内部に点$P$をとると、線分$AP$, $BC$が交わりました。「線分$BP$, $CP$に接し円$\Gamma$に内接する円」を$\Omega_A$、「線分$CP$, $AP$に接し円$\Gamma$に内接する円」を$\Omega_B$、「線分$AP$, $BP$に接し円$\Gamma$に内接する円」を$\Omega_C$と、それぞれ名づけます。円$\Omega_B$と円$\Omega_C$が接するとき、円$\Gamma$と円$\Omega_A$の接点は点$A$に一致することを示してください。
共軸な3円$\omega_0$, $\omega_1$, $\omega_2$があり、円$\omega_0$は円$\omega_1$を、円$\omega_1$は円$\omega_2$を、それぞれ内部に含みます。円$\omega_0$に内接する四角形$ABCD$において、2点$A$, $C$を結ぶ円弧$\gamma_1$, $\gamma_2$, $\gamma_3$, $\gamma_4$と、2点$B$, $D$を結ぶ円弧$\delta_1$, $\delta_2$, $\delta_3$, $\delta_4$が、各々この順に並んでいます。これら8本の円弧がすべて異なり、いずれも円$\omega_1$または円$\omega_2$に接するとき、以下の4円がすべて存在することを示してください。
- 円弧$\gamma_1$, $\gamma_2$, $\delta_1$, $\delta_2$のすべてに接する円。
- 円弧$\gamma_1$, $\gamma_2$, $\delta_3$, $\delta_4$のすべてに接する円。
- 円弧$\gamma_3$, $\gamma_4$, $\delta_1$, $\delta_2$のすべてに接する円。
- 円弧$\gamma_3$, $\gamma_4$, $\delta_3$, $\delta_4$のすべてに接する円。
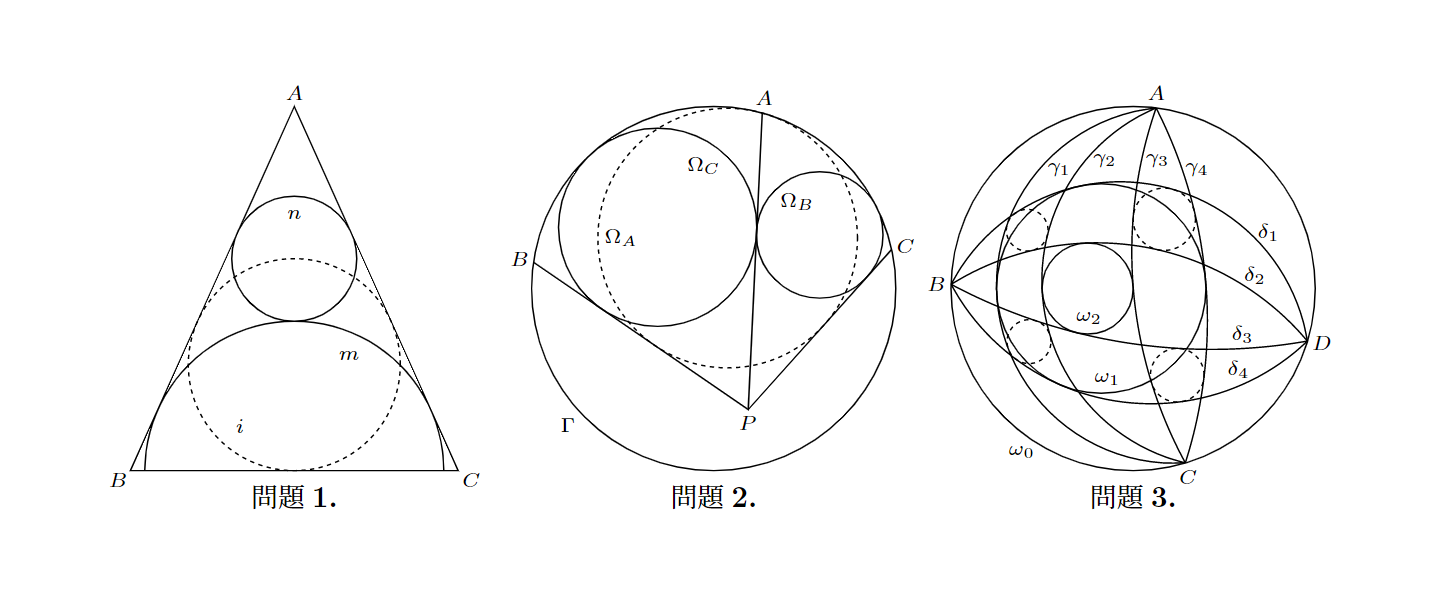
自分で言うことは見苦しいかもしれませんが、どれもこれも凄くシンプルであると思いませんか? 江戸時代の算額のような見た目と言いますか。申し訳ございません、自我が肥大しました。
解説開始
解説をPDFで読みたい方は、 こちら からダウンロードしてください。※2025/12/24追記
LAB01
円$i$, $m$の中心をそれぞれ$I$, $M$とすると、直線$IM$は線分$BC$の垂直二等分線である。点$I$に関し点$M$と対称な点を$N'$とし、「中心が点$N'$であり辺$AB$に接する円」を$n'$で表す。また、3円$i$, $m$, $n'$と辺$AB$との接点をそれぞれ$T_i$, $T_m$, ${T_n}'$とし、線分$IT_i$, $N'T_m$の交点を$X$とする。
いま、点$I$が線分$MN'$の中点であるため、点$T_i$, $X$はそれぞれ線分$T_m {T_n}'$, $N'T_m$の中点である。したがって、三角形$N'MT_m$, $T_m N' {T_n}'$に各々中点連結定理を用いれば、$2IT_i$$= 2(IX+XT_i)$$= MT_m + N' {T_n}'$と計算できる。$MN' = 2IT_i$より、2円$m$, $n'$は互いに外接すると判明し、ゆえに円$n$, $n'$は一致する(図の対称性から円$n'$は辺$AC$にも接する)。点$N'$は明らかに円$i$上の点であるため、題意が示される。$\blacksquare$
別解
半円$m$の円弧を延長し円$m$を描く。直線$BC$に平行な円$m$の接線は2本存在するため、点$A$に近いほうから順に$l_1$, $l_2$と名づける。また、線分$AB$, $AC$が直線$l_1$と交わる点をそれぞれ$B_1$, $C_1$とおき、半直線$AB$, $AC$が直線$l_2$と交わる点をそれぞれ$B_2$, $C_2$とおく。
3辺がそれぞれ平行であるため、三角形$A B_1 C_1$, $ABC$, $A B_2 C_2$はいずれも相似である。この相似比を$s : t : u$とすれば、円$m$の中心は直線$BC$上に乗るため、$s$, $t$, $u$は等差数列をなす。かつ、円$n$, $i$, $m$はそれぞれ三角形$A B_1 C_1$, $ABC$, $A B_2 C_2$の内接円となるため、等差数列の議論より、これらの中心はある直線上に等間隔で並ばなければならない。ゆえに、 円$i$, $m$, $n$の中心をそれぞれ$I$, $M$, $N$とすれば、2点$M$, $N$は円$i$の中心$I$に関し対称であるため、点$M$が円$i$に乗ることと併せ、題意が示される。$\blacksquare$
LAB02
円$\Omega_B$もしくは円$\Omega_C$が線分$AP$, $BP$, $CP$上にもつ接点をそれぞれ$T_A$,$T_B$, $T_C$とする(円$\Omega_B$と円$\Omega_C$は点$T_A$で外接する)。2円$\Omega_B$, $\Omega_C$の共通外接線のうち線分$T_A A$と交わるほうを$l$とし、「円$\Omega_B$, $\Omega_C$とそれぞれ点$T_C$, $T_B$で接する円」を$\omega$で表す。半直線$T_A A$と円$\omega$の交点を$Q$とし、「点$A$を中心とし点$T_A$を通る円」を$\alpha_1$、「点$Q$を中心とし点$T_A$を通る円」を$\alpha_2$で表す。
円$\alpha_1$における反転を考えると、直交性より、この反転で2円$\Omega_B$, $\Omega_C$は不動である。したがって、図の位置関係に注意すれば、円$\Gamma$はこの反転で直線$l$に写るといえる。また、円$\alpha_2$における反転を考えると、この反転でも2円$\Omega_B$, $\Omega_C$は不動であるから、円$\omega$はこの反転で直線$l$に写る。ゆえに、点$A$を通る円$\Gamma$の接線と点$Q$を通る円$\omega$の接線は、いずれも直線$l$と平行である。点$P$を中心とした相似拡大によって円$\omega$を円$\Omega_A$に重ねることができ、かつこの相似拡大で点$Q$は点$A$に重なるため、題意は明らかに成立する。$\blacksquare$
別解( かえで 氏より)
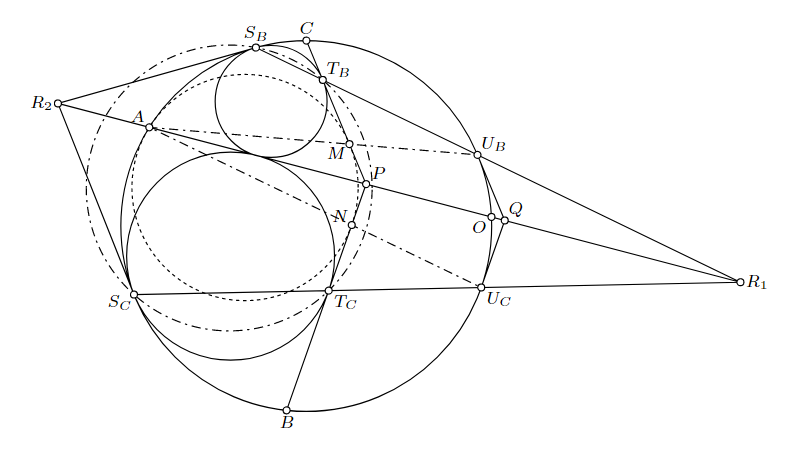
点$T_A$, $T_B$, $T_C$を上の解法と同様にとり、円$\Gamma$と円$\Omega_B$, $\Omega_C$との接点をそれぞれ$S_B$, $S_C$とする。円$\Gamma$と直線$AP$, $S_B T_B$, $S_C T_C$が再び交わる点をそれぞれ$O$, $U_B$, $U_C$とし、直線$AU_C$, $BP$の交点を$M$、直線$AU_B$, $CP$の交点を$N$とする。
有名性質より、点$U_B$, $U_C$における円$\Gamma$の接線は、それぞれ直線$CP$, $BP$と平行である。これら2接線の交点を$Q$とすれば、$QU_B = QU_C$, $PT_B = PT_C$より、三角形$QU_B U_C$と$PT_B T_C$は相似であると判り、特に$T_B T_C \parallel U_B U_C$が導かれる。4点$S_B, U_B, U_C, S_C$は共円であったため、Reimの補題より、4点$S_B, T_B, T_C, S_C$はある円$\gamma$上に存在する。3円$\Omega_B$, $\Omega_C$, $\gamma$の根軸を考えると、3直線$AP$, $S_B T_B$, $S_C T_C$は1点$R_1$で交わるといえる。同様に、3円$\Omega_B$, $\Omega_C$, $\Gamma$の根軸を考えると、2点$S_B$, $S_C$における円$\Gamma$の接線および直線$AP$は1点$R_2$で交わる。点$R_2$での共点から四角形$A S_B O S_C$は調和四角形であり、これと点$R_1$での共点から四角形$A U_B O U_C$も調和四角形である。このことは点$Q$が直線$AO$上に存在することを意味し、三角形$QU_B U_C$と$PNM$は点$A$を中心とし配景の関係をなす。よって、三角形$QU_B U_C$を三角形$PNM$に写す相似変換$f$が存在し、「2直線$QU_B$, $QU_C$に接し点$A$を通る円」、すなわち円$\Gamma$は、変換$f$により「2直線$PT_B$, $PT_C$に接し点$A$で円$\Gamma$と接する円」に写る。これは円$\Omega_A$そのものであるため、題意は明らかに成立する。$\blacksquare$
LAB03
題意の4円がいずれも存在するという性質を、以下「主定理」と呼ぶ。主定理を証明するために、IMO2010 Shortlistより、問題G7を紹介する。以下は筆者が独断で拵えた訳文であるため、原典を確認したければ 公式PDF へアクセスされたい(60ページに掲載されている)。
3本の円弧$\gamma_1$, $\gamma_2$, $\gamma_3$が2点$A$, $C$で交わっている。これらはいずれも直線$AC$によって定まる半平面$H$上に存在し、かつ円弧$\gamma_2$は円弧$\gamma_1$, $\gamma_3$の間を通る。線分$AC$上に点$B$をとり、点$B$を始点とする$H$上の半直線$h_1$, $h_2$, $h_3$を描く。ただし半直線$h_2$が半直線$h_1$, $h_3$の間を通るものとし、半直線$h_i$と円弧$\gamma_j$の交点を$V_{ij}$とおく。ここで、円弧$\widehat{V_{ij}V_{kj}}$, $\widehat{V_{kl}V_{il}}$および線分$V_{kj}V_{kl}$, $V_{il}V_{ij}$によって定まる領域を$\widehat{V_{ij}V_{kj}}\widehat{V_{kl}V_{il}}$で表し、この領域内の円であって4本の境界線すべてに接する円が存在するとき、「$\widehat{V_{ij}V_{kj}}\widehat{V_{kl}V_{il}}$は$\mathit{circumscribed}$である」ということにする。$\widehat{V_{11}V_{21}}\widehat{V_{22}V_{12}}$, $\widehat{V_{12}V_{22}}\widehat{V_{23}V_{13}}$, $\widehat{V_{21}V_{31}}\widehat{V_{32}V_{22}}$がいずれも$\mathit{circumscribed}$であるならば、$\widehat{V_{22}V_{32}}\widehat{V_{33}V_{23}}$も$\mathit{circumscribed}$であることを示せ。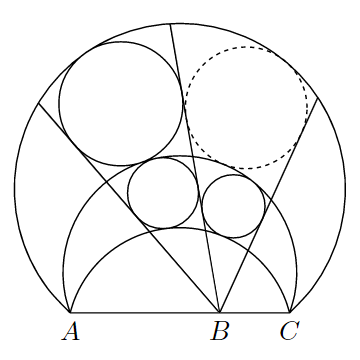
公式解説を参考にしつつ、まずは問題G7の解説を行う。
$i = 1, 2, 3$について、円弧$\gamma_i$の中心を$O_i$, 半径を$R_i$とおく。半平面$H$上の点$P$と直線$AC$の距離を$d(P)$で表し、中心が点$P$であり半径が$r$の円を$\Omega(P, r)$で表す。
$1 \le i < j \le 3$について、まず、円$\Omega(P, r)$が2本の半直線$h_i$, $h_j$の両方に接する場合、どのような性質が成り立つかを考えよう。対称性より、点$P$は半直線$h_i$, $h_j$がなす角の二等分線$\beta_{ij}$上に乗る。点$B$を中心とした相似拡大を考えれば、$r = u_{ij} \cdot d(P)$をみたす定数$u_{ij}$が明らかに存在する。なお、定数$u_{ij}$の具体的な値は半直線$h_i$, $h_j$が直線$AC$となす角によって定まる。
次に、$1 \le i < j \le 3$について、円$\Omega(P, r)$が2本の円弧$\gamma_i$, $\gamma_j$の両方に接する場合、どのような性質が成り立つかを考えよう。有名性質より、点$P$は2焦点$O_i$, $O_j$からの距離の和が$(R_i + R_j)$である点の軌跡として描かれる楕円$\varepsilon_{ij}$上に乗る(この楕円は2点$A$, $C$も通っている)。楕円$\varepsilon_{ij}$の$O_j$側の準線を$l_{ij}$、離心率を$v_{ij}$とおき、点$P$と直線$l_{ij}$の距離を$d_{l_{ij}}(P)$で表せば、
\begin{align*}
r = R_j - (R_j - r) = AO_j - PO_j = v_{ij} \cdot (d_{l_{ij}}(A) - d_{l_{ij}}(P)) = v_{ij} \cdot (d(P) - d(A)) = v_{ij} \cdot d(P)
\end{align*}
という計算から、$r = v_{ij} \cdot d(P)$をみたす定数$v_{ij}$が存在する。
さて、$\mathcal{Q}_{ijkl} \overset{\mathrm{def}}{=} \widehat{V_{ij}V_{kj}}\widehat{V_{kl}V_{il}}$が$\mathit{circumscribed}$であるならば、4本の境界線すべてに接する円は高々1個であるから、これを$\mathcal{I}_{ijkl}$で表す。$\mathcal{I}_{ijkl}$の中心を$O_{ijkl}$、半径を$R_{ijkl}$で表すと、$\mathcal{I}_{ijkl}$は2本の半直線$h_i$, $h_k$に接するため、$R_{ijkl} = u_{ik} \cdot d(O_{ijkl})$なる定数$u_{ik}$が存在する。同様に、$\mathcal{I}_{ijkl}$は2本の円弧$\gamma_j$, $\gamma_l$に接するため、$R_{ijkl} = v_{jl} \cdot d(O_{ijkl})$なる定数$v_{jl}$が存在する。すなわち$u_{ik} = v_{jl}$が成立し、逆に考えれば、$u_{ik} = v_{jl}$のときに限り、$\mathcal{Q}_{ijkl}$は$\mathit{circumscribed}$であるといえる。$\mathcal{Q}_{1122}$, $\mathcal{Q}_{1223}$, $\mathcal{Q}_{2132}$がいずれも$\mathit{circumscribed}$であることから$u_{12} = v_{12}$, $u_{12} = v_{23}$, $u_{23} = v_{12}$がそれぞれ従うため、結局$u_{23} = v_{23}$が成立する。ゆえに$\mathcal{Q}_{2233}$もまた$\mathit{circumscribed}$なのであり、かくして問題G7が解かれる。$\blacksquare$
LABG7で用いた手法は大変有用なものである。具体的な中心や半径を求めずとも、比例定数$u_{ik}$, $v_{jl}$の比較のみで、$\mathcal{Q}_{ijkl}$が$\mathit{circumscribed}$か否かを知ることができる。この手法を応用し、筆者は以下の命題2を得た。
円$\omega_1$の内部に円$\omega_2$があり、2円$\omega_1$, $\omega_2$の根軸上の3点$A$, $B$, $C$がこの順に並んでいる。いま、「点$B$を端点とし$\omega_1$に接する半直線」と「点$B$を端点とし$\omega_2$に接する半直線」が2本ずつ存在するので、それぞれ$h_1$, $h_2$, $h_3$, $h_4$と名づける。また、「2点$A$, $C$を通り$\omega_1$に接する円弧」と「2点$A$, $C$を通り$\omega_2$に接する円弧」が2本ずつ存在するので、それぞれ$\gamma_1$, $\gamma_2$, $\gamma_3$, $\gamma_4$と名づける。ただし、$h_1$, $h_2$, $h_3$, $h_4$および$\gamma_1$, $\gamma_2$, $\gamma_3$, $\gamma_4$が各々この順に並ぶものとする。このとき、以下の4円がいずれも存在する。
- 半直線$h_1$, $h_2$、円弧$\gamma_1$, $\gamma_2$に接する円。
- 半直線$h_1$, $h_2$、円弧$\gamma_3$, $\gamma_4$に接する円。
- 半直線$h_3$, $h_4$、円弧$\gamma_1$, $\gamma_2$に接する円。
- 半直線$h_3$, $h_4$、円弧$\gamma_3$, $\gamma_4$に接する円。
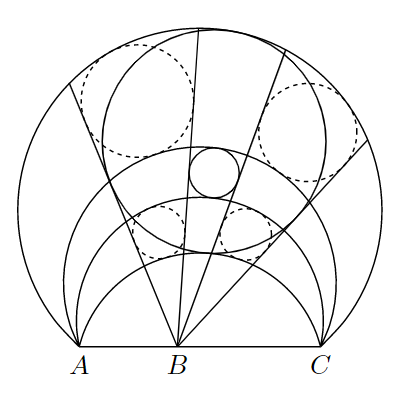
命題2において、$\omega_2$の半径を限りなく小さくすることで、点線で描かれた4円がLABG7と同じ配置になる。この観察は後ほど重要性をもつため、頭の片隅に留めておくことが望ましい。以降、LABG7の解説に倣い、$O_i$, $R_i$, $d(P)$, $\Omega(P, r)$, $\beta_{ij}$, $u_{ij}$, $\varepsilon_{ij}$, $v_{ij}$, $\mathcal{Q}_{ijkl}$, $\mathcal{I}_{ijkl}$, $O_{ijkl}$, $R_{ijkl}$を定義しておく。
定理2を示すべく、補題3、補題4、補題5を以下のように設け、各々証明する。
三角形$ABC$の辺$BC$上に点$D$をとり、「2点$F_1, F_2$を焦点とし点$P$を通る楕円」を$\mathfrak{E}(F_1, F_2; P)$で、楕円$\mathfrak{E}$の離心率を$e_{\mathfrak{E}}$で表す。このとき、以下が成立する。
$$ e_{\mathfrak{E}(B, C; A)} = \frac{e_{\mathfrak{E}(B, D; A)} + e_{\mathfrak{E}(C, D; A)}}{1 + e_{\mathfrak{E}(B, D; A)} e_{\mathfrak{E}(C, D; A)}}$$
まず、$e_{\mathfrak{E}(B, C; A)} = \dfrac{BC}{AB + AC}$であることに注意する($e_{\mathfrak{E}(B, D; A)}$, $e_{\mathfrak{E}(C, D; A)}$も同様である)。三角形$ABC$におけるStewartの定理から、以下が成り立つ。
$$ {AB}^2 \cdot CD + {AC}^2 \cdot BD = ({AD}^2 + BD \cdot CD) BC$$
両辺に$(AB \cdot AC + AC \cdot AD + AD \cdot AB) BC$を加え、変形していく。
\begin{align*}
({\mathrm{LHS}})
&= {AB}^2 \cdot CD + {AC}^2 \cdot BD + (AB \cdot AC + AC \cdot AD + AD \cdot AB) BC \\
&= ({AB}^2 + AB (AC + AD) + AC \cdot AD) CD + ({AC}^2 + AC (AB + AD) + AB \cdot AD) BD \\
&= (AB + AC)(AB + AD) CD + (AB + AC)(AC + AD) BD \\
&= (AB + AC)(AB + AD)(AC + AD)\left(\frac{BD}{AB + AD} + \frac{CD}{AC + AD}\right) \\
&= (AB + AC)(AB + AD)(AC + AD)\left(e_{\mathfrak{E}(B, D; A)} + e_{\mathfrak{E}(C, D; A)}\right) \\
({\mathrm{RHS}})
&= ({AD}^2 + BD \cdot CD) BC + (AB \cdot AC + AC \cdot AD + AD \cdot AB) BC \\
&= ({AD}^2 + AD(AB + AC) + AB \cdot AC + BD \cdot CD) BC \\
&= ((AB + AD)(AC + AD) + BD \cdot CD) BC \\
&= (AB + AC)(AB + AD)(AC + AD) \left(1 + \frac{BD}{AB + AD} \cdot \frac{CD}{AC + AD}\right) \frac{BC}{AB + AC} \\
&= (AB + AC)(AB + AD)(AC + AD) \left(1 + e_{\mathfrak{E}(B, D; A)} e_{\mathfrak{E}(C, D; A)}\right) e_{\mathfrak{E}(B, C; A)}
\end{align*}
$({\mathrm{LHS}}) = ({\mathrm{RHS}})$であるから、補題3が示される。$\blacksquare$
$i \ne m$, $j \ne n$とする。LABG7の図において、$\mathcal{I}_{ijkl}$と$\mathcal{I}_{klmn}$がともに存在すれば、$\mathcal{I}_{ijmn}$が存在する。
点$V_{kl}$(半直線$h_k$と円弧$\gamma_l$の交点)を通る直線$AC$の平行線$p$を引き、半直線$h_i$との交点を$D_i$、直線$\beta_{ik}$, $\beta_{im}$, $\beta_{km}$との交点をそれぞれ$D_{ik}$, $D_{im}$, $D_{km}$とする。点$B$から直線$p$に下ろした垂足を$K_0$とし、点$D_{ik}$, $D_{km}$から半直線$h_k$に下ろした垂足をそれぞれ$K_{ik}$, $K_{km}$とし、さらに点$D_{im}$から直線$h_i$に下ろした垂足を$K_{im}$とする。
いま、4点$(B, K_0, D_{ik}, K_{ik})$は共円である。したがって、$u_{ik} = \dfrac{R_{ijkl}}{d(O_{ijkl})} = \dfrac{D_{ik}K_{ik}}{BK_0} = \dfrac{D_{ik}V_{kl}}{BV_{kl}}$を得ることができる。同様に、4点$(B, K_0, D_{km}, K_{km})$は共円であるから、$u_{km} = \dfrac{D_{km}V_{kl}}{BV_{kl}}$を得る。4点$(B, K_0, D_{im}, K_{im})$の共円からは、$u_{im} = \dfrac{D_{im}D_i}{BD_i}$を得る。円$B D_{ik} D_{km}$と半直線$h_k$が再び交わる点を$E_k$とおけば、$\measuredangle E_k D_{km} D_{ik} = \measuredangle E_k B D_{ik} = \measuredangle D_{ik} B D_i$より、直線$D_{km} E_k$と半直線$\beta_{ik}$の交点$F_{ik}$は円$B D_i D_{km}$上に存在する。簡単な角度計算より三角形$B D_{im} D_i$と三角形$B D_{km} F_{ik}$は相似であると判明し、ここから$u_{im}$の値を以下のように導出できる。
\begin{align*}
u_{im} = \frac{D_{im}D_i}{BD_i} = \frac{D_{km}F_{ik}}{BF_{ik}}
= \frac{D_{km}F_{ik}}{BF_{ik}} = \frac{D_{km}D_{ik}}{BE_k}
= \frac{D_{km}D_{ik} / BV_{kl}}{1 + E_k V_{kl} / BV_{kl}}
= \frac{u_{ik} + u_{km}}{1 + u_{ik}u_{km}}
\end{align*}
一方、$v_{xy}$は楕円$\varepsilon_{xy}$の離心率であるため、
補題3
より、$v_{jn} = \dfrac{v_{jl} + v_{ln}}{1 + v_{jl}v_{ln}}$が成立する。$\mathcal{I}_{ijkl}$と$\mathcal{I}_{klmn}$の存在性より、$u_{ik} = v_{jl}$, $u_{km} = v_{ln}$であるから、明らかに$u_{im} = v_{jn}$となり、補題4が示される。$\blacksquare$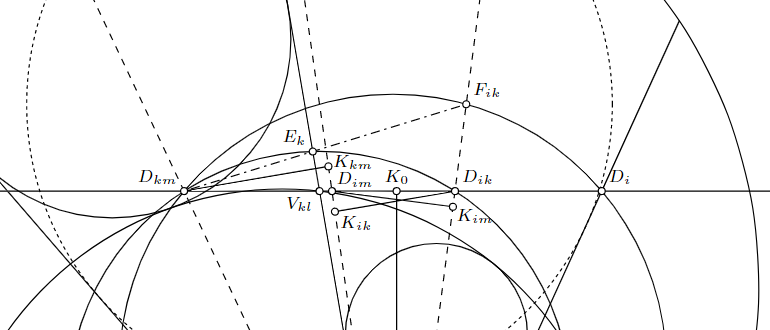
LABG7の図において、$\mathcal{I}_{1122}$, $\mathcal{I}_{1223}$, $\mathcal{I}_{1133}$がいずれも存在するとき、$\mathcal{I}_{1133}$と点円$V_{22}$の根軸は直線$AC$である。逆に、$\mathcal{I}_{1133}$と点円$V_{22}$の根軸が直線$AC$となるように$h_1$, $h_2$, $h_3$および$\gamma_1$, $\gamma_2$, $\gamma_3$を定めれば、$\mathcal{I}_{1122}$, $\mathcal{I}_{1223}$, $\mathcal{I}_{2132}$, $\mathcal{I}_{2233}$がいずれも存在する。
補題4
に$(i, j, k, l, m, n) = (2, 2, 1, 3, 3, 1), (2, 2, 1, 1, 3, 3)$を代入して考えれば、$\mathcal{I}_{1122}$, $\mathcal{I}_{1223}$, $\mathcal{I}_{1133}$がいずれも存在するとき、$\mathcal{I}_{2132}$, $\mathcal{I}_{2233}$も存在し、$u_{12} = u_{23}$$= v_{12} = v_{23}$$= w$をみたす定数$w$が存在する。
補題4
の証明で行った議論より、$u_{13} = v_{13} = \dfrac{2 w}{1 + w^2}$と表せることを確認しておく。
さて、$O_1 O_2 = v_{12} \cdot (R_1 + R_2)$, $O_2 O_3 = v_{23} \cdot (R_2 + R_3)$および$v_{12} = v_{23} = w$より、
\begin{align*}
\left\{ \begin{array}{l}
O_1 O_3 = O_1 O_2 + O_1 O_3 = w \cdot (R_1 + 2 R_2 + R_3) \\
O_1 O_3 = v_{13} \cdot (AO_1 + AO_3) = \frac{2 w}{1 + w^2} \cdot (R_1 + R_3)
\end{array} \right.
\Longrightarrow 2 R_2 = \frac{1 - w^2}{1 + w^2} \cdot (R_1 + R_3)
\end{align*}
となる。楕円$\varepsilon_{13}$の長軸の長さが$(R_1 + R_3)$であり、離心率$v_{13}$が$\dfrac{2 w}{1 + w^2} = \sqrt{1 - \left( \dfrac{1 - w^2}{1 + w^2} \right)^2}$であることから、この式は楕円$\varepsilon_{13}$の短軸の長さが$2 R_2$であることを意味する。楕円$\varepsilon_{13}$は2点$A, C$を通るため、直線$AC$を基準とし円弧$\gamma_2$を$\dfrac{1 + w^2}{1 - w^2}$倍に引き延ばした図形は、楕円$\varepsilon_{13}$のうち半平面$H$上にある部分と一致する。
一方、点$V_{22}$を通る直線$AC$の平行線を引き、半直線$h_1$との交点を$D_1$、直線$\beta_{12}$, $\beta_{13}$, $\beta_{23}$との交点をそれぞれ$D_{12}$, $D_{13}$, $D_{23}$とすれば、LABG7の証明で行った議論より、$u_{12} = \dfrac{D_{12}V_{22}}{BV_{22}}$および$u_{23} = \dfrac{D_{23}V_{22}}{BV_{22}}$が成り立つ。$u_{12} = u_{23} = w$より、$V_{22}$は線分$D_{12} D_{23}$の中点となる。いま、円$B D_{12} D_{23}$の点$D_{12}$における接線と点$D_{23}$における接線の交点$J$をとり、線分$BJ$と直線$D_{12} D_{23}$、円$B D_{12} D_{23}$の交点をそれぞれ$L_1$, $L_2 \; (\ne B)$とおく。有名性質より、直線$BJ$は三角形$B D_{12} D_{23}$の類似中線であるため、直線$BV_{22}$が三角形$B D_{12} D_{23}$の中線であることと併せれば、半直線$BJ$は直線$\beta_{13}$のうち半平面$H$上にある部分と一致する。類似中線の有名性質より、三角形$B V_{22} D_{12}$と三角形$D_{12} V_{22} L_2$は相似であり、ここから$\dfrac{L_1 L_2}{B L_1} = \dfrac{L_2 V_{22}}{B V_{22}} = w^2$を得る。加えて、4点$J, L_2, L_1, B$は調和点列をなすため、
$$ \frac{L_1 L_2}{B L_1} = \frac{J L_2}{BJ} = w^2 \Longrightarrow B L_1 : L_1 L_2 : L_2 J = (1 - w^2) : (w^2 - w^4) : (w^2 + w^4)$$
が従う。すなわち、$\dfrac{d(J)}{d(V_{22})} = \dfrac{d(J)}{d(L_1)} = \dfrac{1 + w^2}{1 - w^2}$と判り、$V_{22} J \perp AC$に則れば、点$J$は楕円$\varepsilon_{13}$上に存在する。結局、直線$\beta_{13}$と楕円$\varepsilon_{13}$の半平面$H$上の交点は点$J$そのものであり、$O_{1133} = J$が導かれる。
類似中線の有名性質より、2点$V_{22}$, $J$からの距離の比が$D_{12} V_{22} : D_{12} J$であるような点の軌跡(Apolloniusの円)は円$B D_{12} D_{23}$である。$\mathcal{I}_{1133}$と直線$h_1$の接点を$T_1$とおくと、
$$ \frac{BT_1}{B O_{1133}} = \cos \angle O_{1133} B D_1 = \cos \angle D_{12} B D_{23} = \cos \angle V_{22} D_{12} J = \frac{D_{12} V_{22}}{D_{12} J} = \frac{B V_{22}}{BJ}$$
と計算できる。$O_{1133} = J$から$BT_1 = BV_{22}$であり、これは点$B$が$\mathcal{I}_{1133}$と点円$V_{22}$の根軸$r$に乗ることを意味する。$O_{1133} V_{22} \perp AC$を思い出せば、直線$AC$と根軸$r$の一致が証明される。
最後に、この逆を示す。すなわち、$\mathcal{Q}_{1133}$の形状を固定し、拘束条件にとらわれず点$V_{22}$を任意に動かす操作を考えれば、この操作で半直線$h_1$, $h_3$および円弧$\gamma_1$, $\gamma_3$は不動であり、半直線$h_2$および円弧$\gamma_2$は点$V_{22}$に追従して動く。$\mathcal{I}_{1122}$, $\mathcal{I}_{1223}$, $\mathcal{I}_{2132}$, $\mathcal{I}_{2233}$がいずれも存在するためには、$u_{12} = u_{23}$かつ$v_{12} = v_{23}$が成り立つことが必要十分である。$h_2$を$h_1$に近づけたとき、2つの半直線$h_1$, $h_2$がなす角は単調減少し、2つの半直線$h_2$, $h_3$がなす角は単調増加する。然れば、$u_{12}$は単調減少し、$u_{23}$は単調増加するため、$u_{12} = u_{23}$となる$h_2$の位置は一意である。同様に、$\gamma_2$を$\gamma_1$に近づけたとき、楕円$\varepsilon_{12}$の離心率$v_{12}$は単調減少し、楕円$\varepsilon_{23}$の離心率$v_{23}$は単調増加するため、$v_{12} = v_{23}$となる$\gamma_2$の位置は一意である。結局、$\mathcal{Q}_{1133}$の形状と$V_{22}$の位置は一対一に対応し、既に示した補題5の前半の内容により、補題5の全体が示される。$\blacksquare$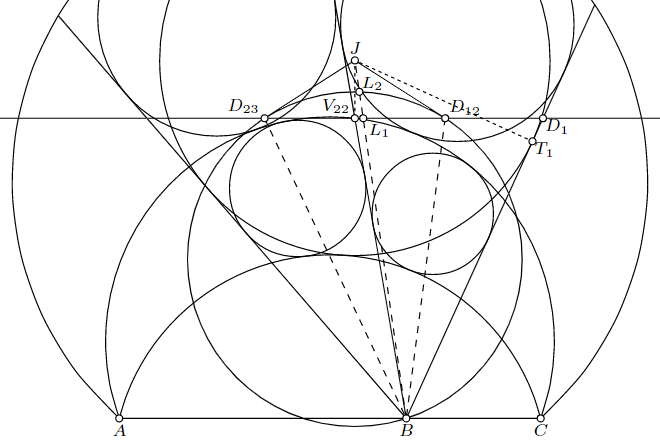
LABM2の証明にあたり、従来の定義を用い、より可読性の高い同値な主張に書き換えておく。
2円$\mathcal{I}_{1144}$, $\mathcal{I}_{2233}$の根軸が直線$AC$であるならば、4円$\mathcal{I}_{1122}$, $\mathcal{I}_{1324}$, $\mathcal{I}_{3142}$, $\mathcal{I}_{3344}$がいずれも存在する。
$\mathcal{Q}_{2233}$の内部の点であって、その点で定まる点円と$\mathcal{I}_{2233}$との根軸が直線$AC$に一致するような点$V_{55}$をとる。半直線$BV_{55}$を$h_5$で表し、2点$A, C$を両端とし点$V_{55}$を通る円弧を$\gamma_5$で表す。すると、 補題5 の逆およびLABG7の主張より、4つの領域$\mathcal{Q}_{2255}$, $\mathcal{Q}_{2553}$, $\mathcal{Q}_{5235}$, $\mathcal{Q}_{5533}$はいずれも$\mathit{circumscribed}$である。条件から、点円$V_{55}$と$\mathcal{I}_{1144}$との根軸もまた直線$AC$に一致する。ゆえに再び 補題5 の逆を用いることができ、4つの領域$\mathcal{Q}_{1155}$, $\mathcal{Q}_{1554}$, $\mathcal{Q}_{5145}$, $\mathcal{Q}_{5544}$はいずれも$\mathit{circumscribed}$である。よって、$\mathcal{I}_{1155}$, $\mathcal{I}_{2255}$がともに存在するため、 補題4 より、$\mathcal{I}_{1122}$も存在する。同様にして$\mathcal{I}_{1324}$, $\mathcal{I}_{3142}$, $\mathcal{I}_{3344}$も存在することが判明し、命題2が示される。
最後に、補題6を設ける。補題6により、主定理とLABM2の関係が明かされる。
任意の円$\mu$における反転で、共軸な3円の組$(\kappa_1, \kappa_2, \kappa_3)$は共軸な3円の組$(\lambda_1, \lambda_2, \lambda_3)$に写る。
円$\mu$における反転で図形$X$が写る先を$X^{-1}$で表すことにする。$(\kappa_1, \kappa_2, \kappa_3)$が2点$K_1$, $K_2$で交わる場合、$(\lambda_1, \lambda_2, \lambda_3)$は明らかに2点${K_1}^{-1}$, ${K_2}^{-1}$を通るため、これら3円は共軸である。$(\kappa_1, \kappa_2, \kappa_3)$が1点で接する場合も同様に考えればよい。$(\kappa_1, \kappa_2, \kappa_3)$が共有点を持たない場合、根軸の有名性質より、ある2点$A_1$, $A_2$によって定まるApolloniusの円の束$\mathfrak{C}$のうち、$\kappa_1, \kappa_2, \kappa_3$のすべてを含むものが存在し、かつ2点$A_1$, $A_2$を通る任意の円は束$\mathfrak{C}$に含まれる円すべてと直交する。反転変換では点まわりの角度が保存されるため、2点$A_1$, $A_2$を通る円の束$\mathfrak{D}$について、束$\mathfrak{D}^{-1}$に含まれる円は束$\mathfrak{C}^{-1}$に含まれる円と直交し、したがって$\lambda_1, \lambda_2, \lambda_3$は2点${A_1}^{-1}$, ${A_2}^{-1}$によって定まるApolloniusの円の束に含まれるといえる。ゆえに、反転後の根軸は線分${A_1}^{-1}{A_2}^{-1}$の垂直二等分線であり、補題6が示される。$\blacksquare$
いよいよ主定理を証明する。主定理の図において、点$D$を中心とする半径任意の円$\nu$を描き、円$\nu$で与図全体を反転しよう。すると、$(\omega_0, \omega_1, \omega_2)$は共軸な円の組であったため、 補題6 よりこれらは反転後も共軸関係を保つ。また、円$\omega_0$および円弧$\delta_1$, $\delta_2$, $\delta_3$, $\delta_4$は反転によって直線に写るため、結局この反転を行うことで、主定理の図はLABM2の図そのものとなる。LABM2は既に証明済みであり、かくして主定理が示される。$\blacksquare$
別解( Melid 氏より)
対称性より、4本の円弧$\gamma_1$, $\gamma_2$, $\delta_1$, $\delta_2$のすべてに接する円$\mathcal{J}_{1122}$が存在することを示せば、その他の円の存在性も同様に導かれる。円弧$\gamma_1$, $\delta_1$と円$\omega_1$の接点をそれぞれ$S_1$, $T_1$とし、円弧$\gamma_2$, $\delta_2$と円$\omega_2$の接点をそれぞれ$S_2$, $T_2$とする。円$\omega_0$, $\omega_1$, $\omega_2$の中心をそれぞれ$O_0$, $O_1$, $O_2$とし、円弧$\gamma_1$, $\gamma_2$, $\delta_1$, $\delta_2$の中心をそれぞれ$\Gamma_1$, $\Gamma_2$, $\Delta_1$, $\Delta_2$ とする。また、以下の補題7および補題8を設ける。
異なる2点で交わる2円$\Omega_A$, $\Omega_B$につき、その中心をそれぞれ$O_A$, $O_B$とする。円$\Omega_A$, $\Omega_B$の内相似中心を$K_i$、外相似中心を$K_e$とし、円$\Omega_A$, $\Omega_B$上にそれぞれ点$T_A$, $T_B$をとる。このとき、以下が成立する。
(1) (3点$T_A$, $T_B$, $K_i$ が共線であり、かつ2点$T_A$, $T_B$が点$K_i$に関し同じ側にある)$\Longleftrightarrow$ (2円$\Omega_A$, $\Omega_B$の一方に内接し、もう一方に外接する、2点$T_A$, $T_B$を通る円が存在する)
(2) (3点$T_A$, $T_B$, $K_e$ が共線であり、かつ点$T_A$, $T_B$がそれぞれ円$\Omega_B$, $\Omega_A$の内部に存在する) $\Longleftrightarrow$ (2円$\Omega_A$, $\Omega_B$の双方に内接し、2点$T_A$, $T_B$を通る円が存在する)
まず、(1)の右向きの矢印を示す。2直線$O_A T_A$, $O_B T_B$の交点を$O$とすれば、Menelausの定理より$\dfrac{O_A K_i}{K_i O_B}\cdot\dfrac{O_B T_B}{T_B O}\cdot\dfrac{O T_A}{T_A O_A} = 1$を得る。点$K_i$は内相似中心であったため、$\dfrac{O_A K_i}{O_B K_i} = \dfrac{O_A T_A}{O_B T_B}$となり、$O T_A = O T_B$が導かれる。ゆえに、中心が点$O$であり点$T_A$を通る円を描けば、これこそが条件をみたす円であり示される。次に、(2)の右向きの矢印を示す。先程と同様に点$O$をとれば、$\dfrac{O_A K_e}{K_e O_B}\cdot\dfrac{O_B T_B}{T_B O}\cdot\dfrac{O T_A}{T_A O_A} = 1$および$\dfrac{O_A K_e}{O_B K_e} = \dfrac{O_A T_A}{O_B T_B}$が判る(点$K_e$は外相似中心である)。ゆえに、再び$O T_A = O T_B$が導かれ、こちらも示される。最後に(1)・(2)の左向きの矢印を示せばよいが、これらはMonge-d'Alembertの定理の主張そのものである。以上の議論を統合し、補題7が示される。$\blacksquare$
4つの接点$S_1$, $S_2$, $T_1$, $T_2$は、いずれもある円$\psi$上に存在する。
3円$\omega_0$, $\omega_1$, $\omega_2$の根軸が直線$AC$と交わる点を$E$とすれば、3円$\omega_0$, $\gamma_1$, $\gamma_2$の根軸は直線$AC$であるため、点$E$は5円$\omega_0$, $\omega_1$, $\omega_2$, $\gamma_1$, $\gamma_2$の根心となる。また、直線$S_1 S_2$が円$\omega_2$と再び交わる点を$F$とすれば、三角形$E S_1 S_2$と三角形$O_2 F S_2$は底辺が同一直線上に乗る二等辺三角形の組であると観察される。根心の性質から$E S_1 \perp O_1 S_1$, $E S_2 \perp O_2 S_2$が従い、これと先程の観察から$E S_1 \perp F O_2$、すなわち$O_1 S_1 \parallel F O_2$が得られる。
よって、2直線$O_1 O_2$, $S_1 S_2$の交点を$P$とおけば、三角形$P O_1 S_1$と三角形$P O_2 F$は点$P$を中心とした相似拡大で写りあうため、点$P$は2円$\omega_1$, $\omega_2$の内相似中心である。対称性より、直線$T_1 T_2$もまた内相似中心$P$を通っている。いま、直線$T_1 T_2$が円$\omega_2$と再び交わる点を$G$とすれば、点$P$は内相似中心であったため、$T_1 S_1 \parallel FG$が容易に判る。4点$F$, $G$, $S_2$, $T_2$はいずれも円$\omega_2$上に存在することから、Reimの補題より、4点$S_1$, $S_2$, $T_1$, $T_2$もまた共円であると導かれ、補題8が示される。$\blacksquare$
直線$S_1 S_2$, $\Gamma_1 \Gamma_2$の交点を$X$、直線$T_1 T_2$, $\Delta_1 \Delta_2$の交点を$Y$とし、直線$T_1 S_1$, $\Gamma_1 \Delta_1$の交点を$Z$とする。以降、円弧$\gamma_n$, $\delta_n$を延長して得られる円をそれぞれ円$\gamma_n$, $\delta_n$で表す($n = 1, 2, 3, 4$)。
3円$\omega_1$, $\omega_2$, $\gamma_1$にMonge-d'Alembertの定理を用いれば、2円$\omega_2$, $\gamma_1$の内相似中心$Q$は直線$S_1 P$上に乗るといえる。また、3円$\omega_2$, $\gamma_1$, $\gamma_2$にもMonge-d'Alembertの定理を用いれば、2円$\gamma_1$, $\gamma_2$の内相似中心$X'$は直線$S_2 Q$上に乗るといえる。2点$S_2$, $Q$はいずれも直線$S_1 P$の点であったから、5点$S_1$, $S_2$, $P$, $Q$, $X'$の共線が得られる。点$X'$は明らかに直線$\Gamma_1 \Gamma_2$の点であり、ここから$X = X'$が従う。
すなわち、点$X$は2円$\gamma_1$, $\gamma_2$の内相似中心である。対称性より、点$Y$は2円$\delta_1$, $\delta_2$の内相似中心である。加えて、Monge-d'Alembertの定理を3円$\omega_1$, $\gamma_1$, $\delta_1$に適用し、2円$\gamma_1$, $\delta_1$の外相似中心$Z'$は$Z = Z'$をみたす($X = X'$の証明と同様に考えよ)。各円の中心と接点に注目すれば、3直線$O_0 P$, $\Gamma_1 S_1$, $\Delta_1 T_1$ はいずれも点$O_1$を通るといえる。ゆえに、三角形$O_0 \Gamma_1 \Delta_1$と三角形$P S_1 T_1$は点$O_1$を中心とした配景の関係をなし、2直線$\Gamma_1 \Gamma_2$, $\Delta_1 \Delta_2$はともに点$O_0$を通るため、Desarguesの定理より、3点$X$, $Y$, $Z$の共線が明かされる。
円弧$\gamma_1$, $\delta_1$とそれぞれ点$\Omega_1$, $\Omega_2$で内接し、円弧$\gamma_2$と点$\Omega_3$で外接する円を$\Omega$とする(このような3点$\Omega_1$, $\Omega_2$, $\Omega_3$のとり方は一意である)。
補題7
より、3点$\Omega_1$, $\Omega_3$, $X$は共線である。直線$\Omega_1 \Omega_3$, $S_1 S_2$が円$\gamma_1$と再び交わる点をそれぞれ${\Omega_1}', {S_1}'$とし、$\dfrac{\Gamma_2 X}{\Gamma_1 X} = c$とすれば、点$X$が内相似中心であることより、
\begin{align*}
X \Omega_1 \times X \Omega_3 &= X \Omega_1 \times (c \cdot X {\Omega_1}') = c \cdot X \Omega_1 \times X {\Omega_1}' \\
&= c \cdot X S_1 \times X {S_1}' = X S_1 \times (c \cdot X {S_1}') = X S_1 \times X S_2
\end{align*}
と計算される。同様に、$Z \Omega_1 \times Z \Omega_2 = Z T_1 \times Z S_1$である。
補題8
より、4点$S_1$, $S_2$, $T_1$, $T_2$は円$\psi$上の点であるため、上記の計算より、2円$\Omega$, $\psi$ の根軸は直線$XZ$に一致する。したがって、直線$Y \Omega_2$と円$\Omega$が再び交わる点を$\Omega_4$とすれば、点$Y$は根軸$XZ$上の点であるから、$Y T_1 \times Y T_2 = Y \Omega_2 \times Y \Omega_4$が成立する。3点$\Omega_2$, $\Omega_4$, $Y$の共線より、
補題7
を適用でき、円$\Omega$と円弧$\delta_2$は接点$\Omega_4$をもつ。かくして題意が示された。$\blacksquare$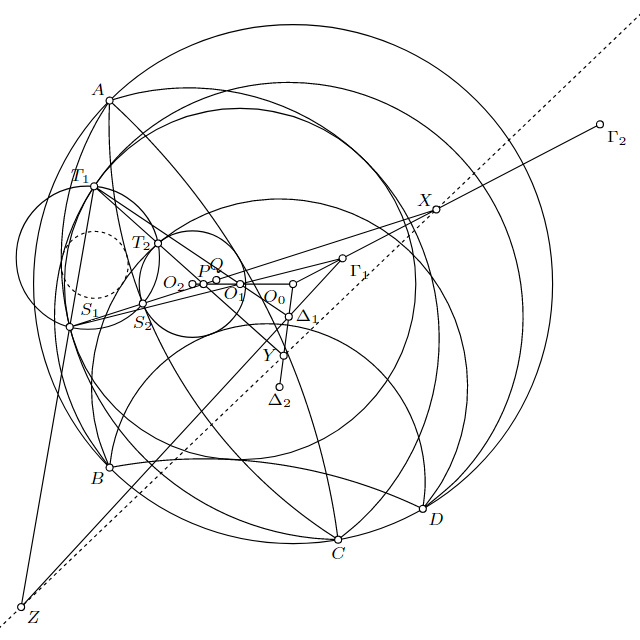
別解( sato2718 氏より、一部改変)※2025/12/24追記
本解の問題G7・補題6の結果はそのまま用い、定理2の証明を目標とする。$i=1,2,3,4$について、半直線$h_i$、円弧$\gamma_i$が円$\omega_1$もしくは円$\omega_2$と接する点を、それぞれ$S_i$, $T_i$とおく。いま、根軸$AC$上の点$X$から2円$\omega_1$, $\omega_2$への方べき(これらは等しい)を${\rm Pow}(X)$で表せば、点$B$は2円$\omega_1$, $\omega_2$の根軸上の点であるため、4点$S_1$, $S_2$, $S_3$, $S_4$は点$B$を中心とする半径$\sqrt{{\rm Pow}(B)}$の円に乗る。円弧$\gamma_1$を基準とし、点円を含む4円$A$, $T_1$, $\omega_1$, $C$についてCaseyの定理を用いれば、$\sqrt{{\rm Pow}(A)} \times CT_1 = \sqrt{{\rm Pow}(C)} \times AT_1$が得られる。他の円弧についても同様に考えることで、$\dfrac{AT_1}{CT_1}=\dfrac{AT_2}{CT_2}=\dfrac{AT_3}{CT_3}=\dfrac{AT_4}{CT_4}=\dfrac{\sqrt{{\rm Pow}(A)}}{\sqrt{{\rm Pow}(C)}}$が従い、4点$T_1$, $T_2$, $T_3$, $T_4$は線分$AC$に関する特定のApolloniusの円に乗るといえる。
ここまでの議論より、「半直線$h_1$, $h_2$とそれぞれ点$S_1$, $S_2$で接する円」、「半直線$h_3$, $h_4$とそれぞれ点$S_3$, $S_4$で接する円」、「円弧$\gamma_1$, $\gamma_2$とそれぞれ点$T_1$, $T_2$で接する円」、「円弧$\gamma_3$, $\gamma_4$とそれぞれ点$T_3$, $T_4$で接する円」をいずれも定義できるため、それぞれ$\sigma_{12}$, $\sigma_{12}$, $\tau_{34}$, $\tau_{34}$と名づけよう。2円$\sigma_{12}$, $\tau_{12}$の外相似中心を$W$とすれば、まず3円$\sigma_{12}$, $\tau_{12}$, $\omega_1$にMonge-d'Alembertの定理を用い、3点$S_1$, $T_1$, $W$の共線を得る。3円$\sigma_{12}$, $\tau_{12}$, $\omega_2$にもMonge-d'Alembertの定理を用いれば、3点$S_2$, $T_2$, $W$の共線を得るため、外相似中心$W$は直線$S_1 T_1$, $S_2 T_2$の交点として描ける。ゆえに、点$W$を中心とする半径$\sqrt{WS_1 \times WT_1}$の円$\rho$における反転で円$\sigma_{12}$と円$\tau_{12}$は互いに写りあうことが判る。接点に注目すれば、2円$\omega_1$, $\omega_2$はいずれも円$\rho$と直交する。すなわち、点$W$から2円$\omega_1$, $\omega_2$への接線の長さは等しく、点$W$は根軸$AC$に含まれる。点$W$を中心とした相似拡大を考えれば、明らかに$u_{12} = v_{12}$である。よって$\mathcal{I}_{1122}$が存在し、同様にして$\mathcal{I}_{1324}$, $\mathcal{I}_{3142}$, $\mathcal{I}_{3344}$も存在する。あとは本解の通りである。$\blacksquare$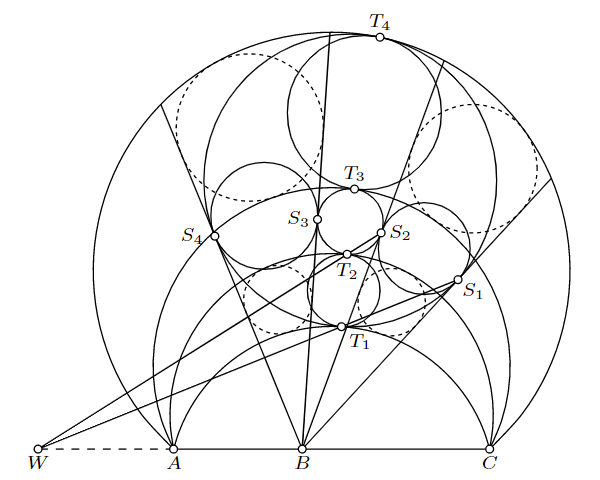
コメント
お疲れ様でした。LAB01から順にコメントしていきたいと思いますが、LAB03のあまりの分量に押し流され、「LAB01って何だっけ?」という状態の読者がいらっしゃるかもしれません……適宜リンクを押してご確認ください。
LAB01
円$i$上の対蹠点(直径の両端にあたる点)として2点$M$, $N$をとり、「中心が点$M$であり辺$AB$に接する円」を$m$、「中心が点$N$であり辺$AB$に接する円」を$n$としても、2円$m$, $n$は互いに接します。この一般化は$AB \\ne AC$の場合にも成り立ち、かつ証明は元の問題と同様に行えるのですが、それでも敢えて$AB = AC$の場合を出題した理由は、偏に問題の見た目が洗練され、参加者の解答意欲向上を見込めると考えたためです。結果的に、本問の解答提出数は他2問を大きく上回りました。目論見が見事に叶ったといえますね。
LAB02
個人的には、本コンテストにおける良問枠です。「2本の直線および1つの円に接する円」はcurvilinear incircleと呼ばれ(より広義に「計3本の直線・円のすべてに接する円」と定義する例もみられます)、有名なmixtilinear incircleの拡張となっているわけですが、本問はcurvilinear incircleを題材とし、かつ主張・証明とも非常にシンプルに仕上がった一品です。経験を積めば積むほどに避けたくなる試みが、実は本問の最適解へ繋がる初手でした。なお、本解の接線$l$を描いた参加者・円$\omega$を描いた参加者が、1名ずついらっしゃったことは、私にとって驚異となりました。
ところで、ここまでシンプルな性質であれば、何らかの先行研究を発見することが常であるといえます。しかしながら、意外にも
Euclidean Geometry
(By Paul Yiu) という文献の99ページに弱い主張(mixtilinear incircleの場合のみを考えたもの)の掲載が認められる点を除いては、curvilinear incircleに関する70件以上の文献渉猟で類題に全く出会えませんでした。もしも先行研究をご存じの方がいらっしゃれば、是非ともご一報ください。
LAB03
LABG7の問題図を拝見した際に、「$\widehat{V_{11}V_{31}}\widehat{V_{33}V_{13}}$も何となく$\mathit{circumscribed}$であるように見えるなぁ」と直感しました(なぜ?)。2025年の夏頃からその証明に取り掛かり、いくつかの副産物にも恵まれつつ、初秋になりやっと証明できました。そこから主産物・副産物を組み合わせ、同年晩秋に本問が完成した、という次第です。コンテスト期間に
投票
を行い、「見た目で選ぶ、お気に入りの問題」で3問中の最多得票となったことは記憶に新しいですね。
そもそもLABG7の時点で当該年度のShortlistにおける(幾何分野内の)最難関であり、さらなる強化版という立ち位置ゆえに、Testerからも「IMOで出題される難易度は超えている」との講評をいただいております。有名事実かのように挙げた
補題3
さえも、現時点で先行研究に出会えておらず、筆者は自力で発見するしかなかったものです。なお、Melid氏の別解はMonge-d'Alembertの定理を極限まで活用し、sato2718氏の別解は本解を辿りつつも係数比較を巧妙に簡略化し、いずれも非常にエレガントなものといって差し支えありませんが、それに比べ本解のエレファントさは何だ大変けしからん全方面へ謝罪せよ。
締め括り
以上がT-DEMO Show 2025の全容となります。今回出題した全3問は、「接する円の性質」といった共通のテーマを有しています。所謂接円問題にも難易度・アプローチにこれだけの幅広さがある、という教訓を、実感とともに胸中へ留めていただければ幸いです。
感想・指摘等がございましたら、コメントでお知らせください。改めて、ご参加/ご観覧ありがとうございました。追加予定の部分は年内に反映します。※2025/12/24追記:反映しました。
