平面上の凸な領域を3本の直線で面積7等分できない(後編)
本記事は 日曜数学 Advent Calendar 2023 の5日目の記事です。
前編のおさらい
前編 では
平面上の凸な領域を3本の直線で面積7等分することはできない
という予想をたて、証明の準備として、
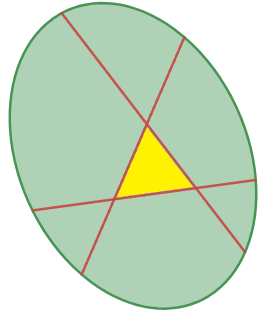 コアが正三角形で凸な領域を7分割する例
コアが正三角形で凸な領域を7分割する例
という補題をたてました。「コア」とは今回の記事で用いる呼称で、7分割された領域の中央の三角形の部分のことです。
証明には背理法を使います。まずは「平面上の凸な領域を3本の直線で面積7等分することができる」と仮定してみて、しかしそれでは矛盾が発生してしまうことを示そうというわけです。
記号
まず、証明に使う図の記号を説明します。コアを各辺の長さが1で底辺を水平とした正三角形とし、7分割した領域の面積を$A,B,C,D,E,F,G$とします。
![正三角形のコアと面積!FORMULA[1][544494324][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FeR0PdLY0AsvbLjDOaJaQ.png?alt=media) 正三角形のコアと面積$A,B,C,D,E,F,G$
正三角形のコアと面積$A,B,C,D,E,F,G$
記号が煩雑になるのを避けるために図を分けます。
領域と直線の交点を点$a,b,c,d,e,f$とし、直線同士の交点を$ g,h,i$とします。また、領域の境界線において$b$上で$c$に向かう方向の接線と水平線のなす角を$\theta $とし、$c$上で$b$に向かう方向の接線と水平線のなす角を$\phi $とします。
![点!FORMULA[10][174006459][0]と角度!FORMULA[11][-109163711][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FZhG6sQmfj8huTnY6gghj.png?alt=media) 点$a,b,c,d,e,f,g,h,i$と角度$ \theta,\phi$
点$a,b,c,d,e,f,g,h,i$と角度$ \theta,\phi$
ここからは$A=B=C=D=E=F=G$となるような領域の形を求めようということになります。
線分$g-a$の長さ
まず線分$g-a$の長さに注目します
$A=B=C=D$であれば線分$g-a$の長さは$\sqrt{2}-1$以下となる
![線分!FORMULA[18][36361517][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F3Dbry9uJqe5qoCRpuy8E.png?alt=media) 線分$g-a$
線分$g-a$
背理法を使う
もし仮に線分$g-a$の長さが$\sqrt{2}-1$より大きい場合、$A=B$を満たすためには線分$h-b$の長さは$\sqrt{2}-1$未満でないといけない。なぜなら、そうしないと三角形$iab$の面積が$2A$より大きくなってしまうからである。
線分$h-b$の長さが$\sqrt{2}-1$未満になるということは、$A=B$を満たすために$\theta$は60°未満でないといけない。
一方で$A=D$を満たすためには線分$h-c$の長さは1以下でないといけないし、そうなると$\phi$は90°以下でないといけない。
しかし、上記のもとでは$A=C$を満たせなくなるので、$g-a$の長さは$\sqrt{2}-1$以下となる。
![!FORMULA[36][1220736053][0]のもとで線分!FORMULA[37][36361517][0]の長さを最大化すると!FORMULA[38][-707440430][0]となる](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F07CltuNOngAjj5I2puGG.png?alt=media) $A=B=C=D$のもとで線分$g-a$の長さを最大化すると$\sqrt{2}-1$となる
$A=B=C=D$のもとで線分$g-a$の長さを最大化すると$\sqrt{2}-1$となる
また、対称性より下記がいえます。
$A=B=C=D=E=F$であれば線分$g-a,h-b,h-c,i-d,i-e,g-f$の長さはすべて$\sqrt{2}-1$以下となる
![!FORMULA[42][-1841629340][0]を満たすための点!FORMULA[43][-53380305][0]の位置の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FyMhSt2hyv8teiTPcs0h7.png?alt=media) $A=B=C=D=E=F$を満たすための点$a,b,c,d,e,f$の位置の例
$A=B=C=D=E=F$を満たすための点$a,b,c,d,e,f$の位置の例
ここで線分$g-a_{max},h-b_{max},h-c_{max},i-d_{max},i-e_{max},g-f_{max}$の長さはすべて$\sqrt{2}-1$です。
またこのとき、台形$g-a_{max}-b_{max}-h$の面積は$A$に等しくなることを意識しておいてください。
証明
これでようやく記事タイトルの証明ができます
線分$g-a,h-b$の長さがどちらも$\sqrt{2}-1$以下になるということは$A=B$を満たすためには$ \theta $ は60°以下でないといけない。そうでないと$A>B$となってしまう。
同様に、線分$h-c,i-d$の長さがどちらも$\sqrt{2}-1$以下になるということは$A=D$を満たすためには$ \phi $ は60°以下でないといけない。そうでないと$A>D$となってしまう。
しかし、この条件では$A>C$となってしまう。したがって$A=B=C=D$とはなりえない。
証明できましたので、予想は晴れて定理となり...
本当に証明は完了したのか?
実は上記の証明について、領域の面積が「0より大きく有限の場合」にのみ有効であることに記事を執筆中に気がついしまいました。領域の面積が無限の場合はコアが有限の面積であることから面積7等分できないことを示せそうですが、面積0の場合は、そもそも「線分で領域を分ける」とはどういうことかをまずきちんと定義しないと面積7等分できないことを証明できそうにありません。
私が証明できたのはここまでとなります。
平面上の面積が0より大きく有限で凸な領域を3本の直線で面積7等分できない
記事タイトルに若干の偽りがあることをここに謝罪いたします。
余談
今回は7等分でしたが、6等分について考えますと逆に「 平面上のどんな有限で凸な領域も、必ず直線3本で面積6等分できる 」ということが示せます。
日曜数学アドベントカレンダー、明日はkiguro_masanaoさんの記事を予定しています。
