平面上の凸な領域を3本の直線で面積7等分できない(前編)

序文

私は ケーキに３回だけ刃を入れてできるだけ公平に分割したい話 - アジマティクス という数学記事が大好きで、これを読んで以来、形を切り分ける問題をいろいろと考えています。今回ご紹介するのは、そのうちのひとつです。問題も証明も 私自身が自分で思いついたもの ではありますが、先行研究などは調べていないので、ご存じの方は、ぜひコメント欄で教えてください。

まずは簡単な問題

いきなり解答ですが、できます。具体例としては、たとえば以下のような領域があります。
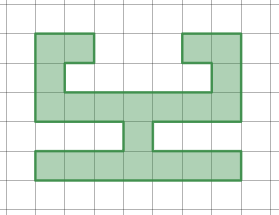直線3本で面積7等分できる領域の例
ほら、こんなふうに。3直線をひけば、もとの領域を面積の等しい7つのパーツに分割できますね。
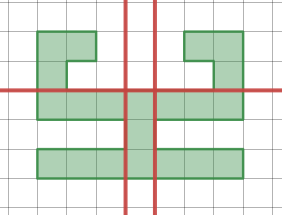直線3本で領域を面積7等分できた

本番の問題

凸ということは、さきほどの領域のように、へこんだところがあってはいけないということです。
少し試行錯誤してみるとわかりますが、どうもできないような気がしてきます。

証明には背理法を使います。まずは「平面上の凸な領域を3本の直線で面積7等分することができる」と仮定してみて、しかしそれでは矛盾が発生してしまうことを示そうというわけです。

準備1 直線はどのように交わるか

まずは面積を等分しなくてもいいので凸な領域を直線3本で7分割する方法を考えます。
領域の形や直線の向きや位置が分からなくても、領域の外周部には3本の直線との交点が必ず合計6個存在することはわかりますね。(この交点は位置が重なる場合もそれぞれカウントするとしています)
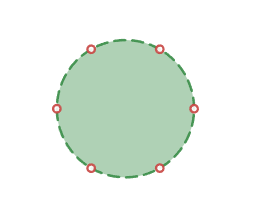領域と直線の6交点
この6個の交点のどれとどれを結んで直線をひくか、また直線同士の交点数をいくつとするかで領域を分割できるパターンを列挙してみると、下記のようになります。(こちらの直線同士の交点は、複数重なる場合に1個カウントとしています)

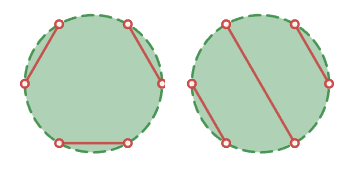直線同士の交点0個で4分割
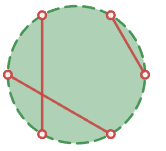直線同士の交点1個で5分割
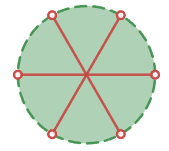直線同士の交点1個で6分割
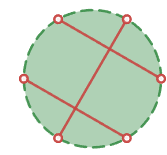直線同士の交点2個で6分割
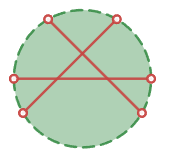直線同士の交点3個で7分割
上記のとおり7分割できるのは1パターンしかありませんので、下記の補題がいえます。

準備2 中央の三角形の形状

さきほどの補題から、もし「平面上の凸な領域を３本の直線で面積７等分することができる」のであれば、中央に三角形の領域ができることになります。この三角形をここでは「コア」と呼ぶことにします。
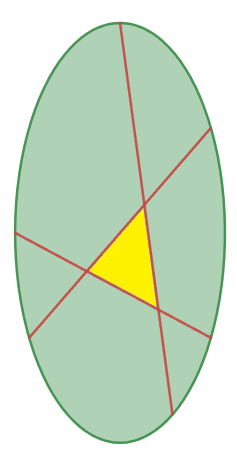コア
このとき全体をアフィン変換してコアを正三角形に変形することができます。平面上のアフィン変換とは、図形を平行移動、回転、特定の向きに伸縮、せん断変形させる変換の組み合わせです。
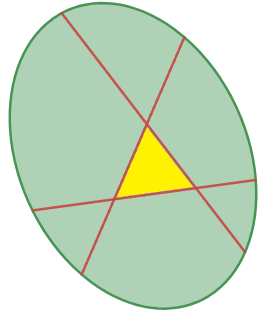正三角形になったコア
さて、アフィン変換しても分割された各領域間の面積比はかわりませんし、凸な領域はアフィン変換しても凸なままなので、下記の補題がいえます。

準備完了

これで、いよいよ証明の準備が整いました。この後は、コアが正三角形であって直線3本で面積7等分ができる領域の形について考えていくことになるわけですが、記事を執筆中にアドベントカレンダーの登録日12/2になってしまいました。この記事は前編として、ここで終わりにします。
後編は12/5に公開します！→ 公開しました！

日曜数学アドベントカレンダーは、明日は108Hassiumさんの記事を予定しています。
それでは！！