ファインマングラフと生成汎関数

どうも、初投稿です。
東京大学理科一類B１のホウジローといいます。駒場理数サークルのアドカレの記事を書いてみたいと思います。今回は私が最近ハマっている、ファインマングラフについての話をしていきます。場の量子論についての話なので、前提知識としては量子力学、解析力学、特殊相対論などは仮定したいですが、前提知識がなくてもある程度内容を追えるように補足は入れていきます。

経路積分

量子力学では、ある状態からある状態への確率振幅を計算するとき、ある経路のみが決定するのではなく、すべての経路について重みづけをして足し合わせることになります。そしてその重みづけは作用汎関数を指数に乗せた形で表されます。
$\bra{\phi_F,t_F}\ket{\phi_I,t_I}=\displaystyle \int_{\phi=\phi_I} ^{\phi=\phi_F}\mathcal{D}\phi \exp{\bigg\{i\int_{t_I}^{t_F} dt\int d^3x \mathcal{L}(\phi) \bigg\}} $
ここで積分測度$\mathcal{D}\phi$は$\phi$についてすべての経路を足し合わせるという意味です。

n点グリーン関数

一般に、粒子の散乱問題を解くときに相互作用などの情報を知るには、n点グリーン関数という量を求める必要があります。これは次のように表されます。
$\frac{\displaystyle \int \mathcal{D}\phi \phi (x_1)\phi (x_1)\cdots \phi (x_n)e^{i\int d^4x \mathcal{L}(\phi)}}{\displaystyle \int \mathcal{D}\phi e^{i\int d^4x \mathcal{L}(\phi)}}$
　具体的な導出はここでは省略しますが、expが確率に対応するものと考えてみると、分子は経路ごとに確率の重みづけをして和をとっていて、分母は規格化因子のように見れると思います。
　この経路積分を計算してグリーン関数を求めたいのですが、相互作用が入っていると厳密に計算をするのは困難です。そこで、自由場のラグランジアンと相互作用項に分けて、摂動計算を行います。つまり、
$ \big\langle \phi(x_1)\cdots \phi(x_n)e^{i\int d^4x\mathcal{L_int}(\phi)} \big\rangle_0=\big\langle \phi(x_1)\cdots \phi(x_n) \displaystyle \sum_{k=0}^{\infty}\frac{1}{k!}\bigg(\int d^4x\frac{-i \lambda }{4!}\phi^4\bigg)^k \big\rangle_0 $

ただし、$ \langle \cdots \rangle_0=\frac{\displaystyle \int \mathcal{D}\phi (\cdots) e^{i\int d^4x \mathcal{L_0}(\phi)}}{\displaystyle \int \mathcal{D}\phi e^{i\int d^4x \mathcal{L_0}(\phi)}} $であり$\mathcal{L_0}(\phi)=\frac{1}{2}\partial^\mu\phi\partial_\mu\phi-\frac{m^2}{2}\phi^2$
と展開します。つまり、自由場のラグランジアン$\mathcal{L_0}$のみを残して相互作用項のみを展開した形です。すると、各項は計算しやすい形になっているので（どう計算するかは後述します）λの低次から計算していき、近似的にグリーン関数を求めることができます。

ファインマングラフの読み方

ファインマングラフとは？

　ではここからファインマングラフの説明に入っていきます。ズバリ、ファインマングラフとは図１のような図形のことで、グリーン関数の摂動計算をした際の項をわかりやすく図示したものです。しかも、ただの計算ツールではなく粒子同士の相互作用を非常にわかりやすくしているとってもえらいツールです。

グラフと式の対応関係

　このグラフの読み方について簡単に説明します。n点グリーン関数であればn個の外側に伸びる線があり、これを外線と呼びます。また４つの線が伸びている頂点は積分されている変数yに対応しています。そして$x_1$から$x_2$に線が伸びていた場合、ファインマンプロパゲーター$\Delta_{F,0}(x_1-x_2)$を含んでいることを表しています。そして線の本数だけプロパゲーターがかけられていることになります。一つ例を見てみましょう。 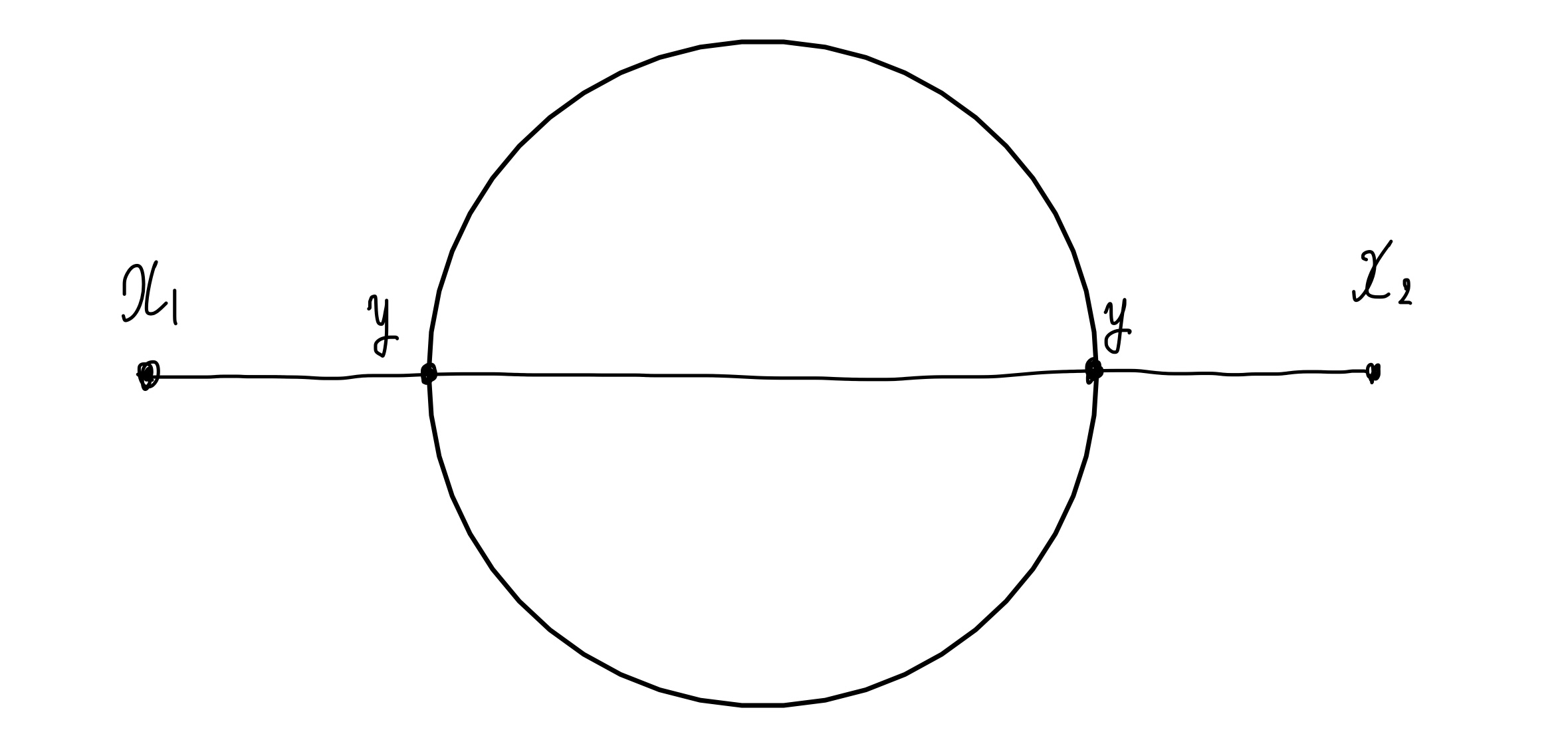ファインマングラフの例
これを式にすると、次のようになります。
$\big(\frac{-i\lambda}{4!}\big)^2\displaystyle \int d^4y_1 \int d^4y_2 (\Delta_{F,0}(y_1-y_2))^3\Delta_{F,0}(x_1-y_1)\Delta_{F,0}(y_2-x_2) $
ここで、線の本数だけプロパゲーターがかかっていて、引数が頂点と対応していることを確認してください。
　次にグリーン関数を摂動計算してファインマングラフで表したいと思います。4点グリーン関数を相互作用結合定数λの0次から順に求めていくとき、0次は以下のようになります。

計算方法

計算方法についてですが、ウィックの定理という便利な定理から計算することができます。

この定理は$\phi(x_i)$と$\phi(x_j)$からファンマンプロパゲーターができるということを示しています。ファインマンプロパゲーターは具体的にわかっているものなので、これを図で表すとファインマングラフでの計算となります。

対称因子

　ここで、それぞれのファインマングラフの係数に注目してみましょう。n点グリーン関数をファインマングラフで表したとき、その係数部の分母は対称因子と呼ばれ、グラフの対称性を反映した数字になっています。
具体例を見てみましょう。下のグラフは4点グリーン関数のλ2次から生まれるグラフです。 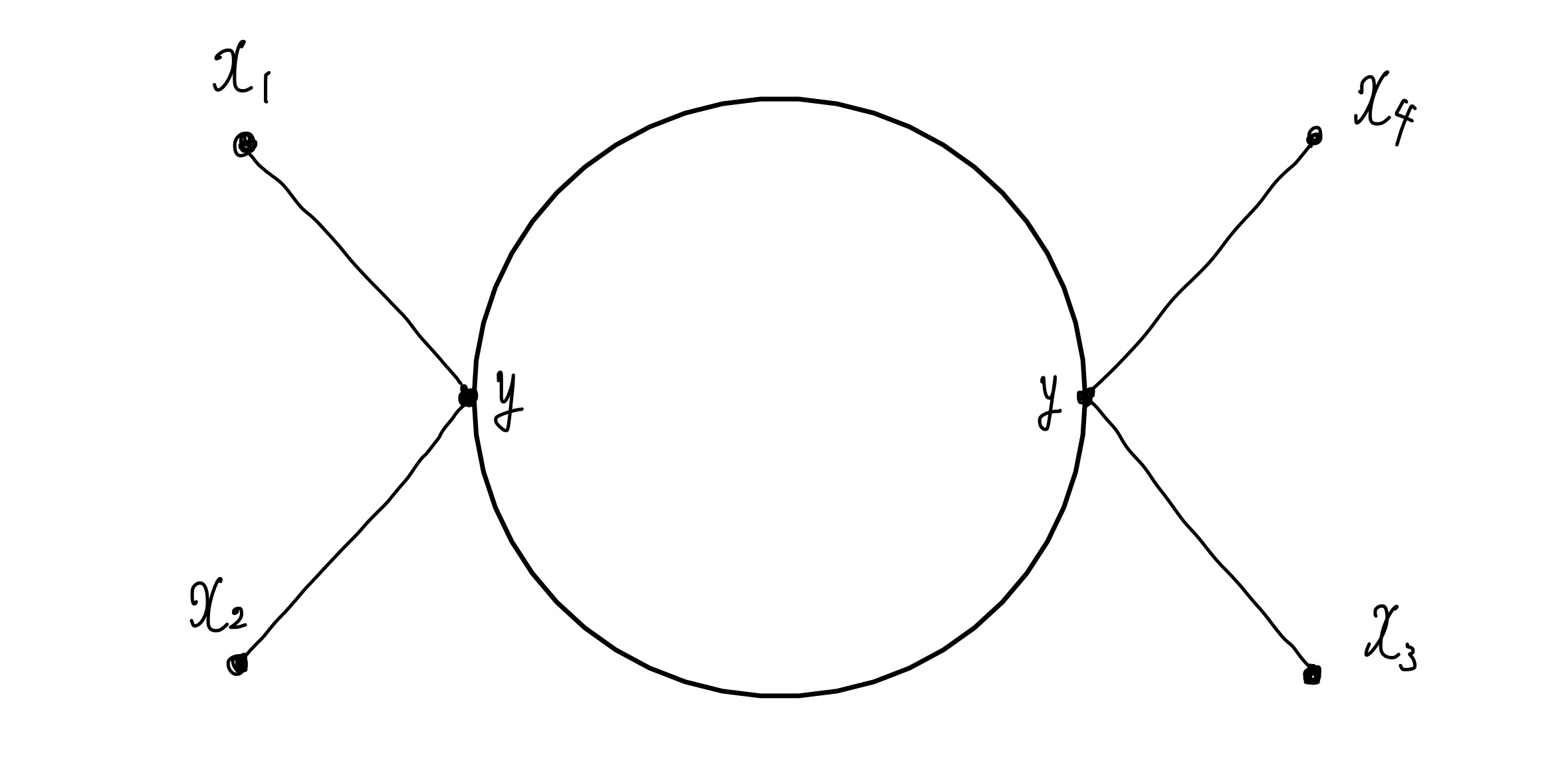４点グリーン関数のλ2次の一例
このグラフで表される項は次のようになります。
$\frac{(-i \lambda )^2}{2}\displaystyle \int d^4y \int d^4y' \Delta_{F,0}(x_1-y)\Delta_{F,0}(x_2-y)\Delta_{F,0}(y'-y)\Delta_{F,0}(y'-y)\Delta_{F,0}(x_3-y')\Delta_{F,0}(x_4-y')$
　ここでは、内線２本が等価でこの入れ替えが２通りなので対称因子は２になっています。

生成汎関数

前節の方法を用いてせかせかと書き下しても面白いのですが、このグラフたち、何かきれいな構造があるように見えませんか？実は、このグラフたちは生成汎関数を考えることでよりまとまった形に書くことができます。

n点グリーン関数の生成汎関数は次のように外場$J(x)$を導入することで表されます。

この関数を$J(x)$について展開したときのn次の係数がn点グリーン関数を与えます。
$Z[J]= \displaystyle\sum_{n=0}^\infty \int dx_1^4 \cdots \int dx_n^4 \frac{iJ(x_1) \cdots iJ(x_n)}{n!}$ $\displaystyle\int \mathcal{D\phi} \phi(x_1) \cdots\phi(x_n)e^{i\int dx^4 \mathcal{L(\phi)}} $
ここで$Z[0]=1$となるように規格化しているので、Zの汎関数微分で次のように表せます。
$ \bra0 T[\hat\phi(x_1) \cdots \hat\phi(x_n)] \ket0 =\frac{1}{i^n}\frac{\delta^nZ[J]} {\delta J(x_1) \cdots \delta J(x_n)} $
ここで、それぞれのファインマングラフの係数に注目してみましょう。n点グリーン関数をファインマングラフで表したとき、その係数部分の分母は対称因子と呼ばれ、グラフの対称性を反映した数字になっています。
具体例を見てみましょう。下のグラフは4点グリーン関数のλ2次から生まれるグラフです。
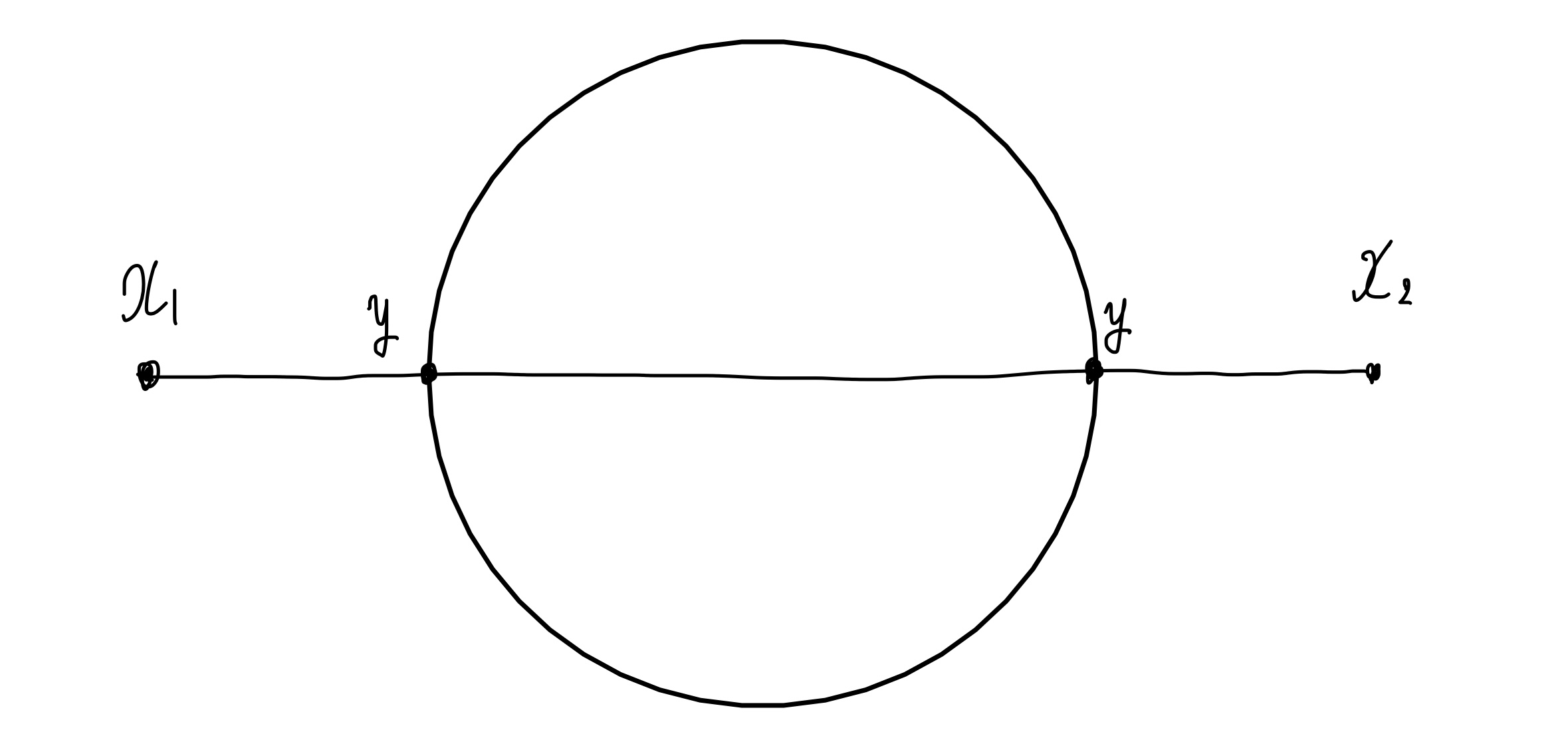グラフの一例
　このグラフでは、中央の３本の内線は等価なので$3!$が対称因子となります。実際に展開して計算すると、係数が$\frac{1}{3!}$となっています！
各々の単連結なグラフに添え字をつけ$\mathcal{C}_i$としその対象因子を$ \mathcal{S}_i$ とおきます。すると任意のグラフは係数込みで次のように表されます。
$ \displaystyle \prod_{i=0}^{\infty} \frac{1}{{n_i}!}\Bigg[\frac{\mathcal{C}_i}{\mathcal{S}_i}\Bigg]^{n_i} $
したがって、これらの和は
$\displaystyle \sum_{n_i=0}^\infty \Bigg(\prod_{i=0}^{\infty} \frac{1}{{n_i}!}\Bigg[\frac{\mathcal{C}_i}{\mathcal{S}_i}\Bigg]^{n_i} \Bigg) =\prod_{i=0}^{\infty} \Bigg( \sum_{n_i=0}^\infty \frac{1}{{n_i}!}\Bigg[\frac{\mathcal{C}_i}{\mathcal{S}_i}\Bigg]^{n_i} \Bigg)=\prod_{i=0}^\infty \exp \Bigg(\frac{\mathcal{C}_i}{\mathcal{S}_i}\Bigg)$
このように、指数の肩に単連結なグラフを乗っけることで、すべてのグラフの和を表現することができました。
これを踏まえて、連結したグラフのみを含む連結グリーン関数の生成汎関数を考えます。先ほどの議論から、指数の肩には連結なグラフのみが存在しているので、生成汎関数$W[J]$は次のように定義されます。

このように定義することで、元のグリーン関数を単連結なグリーン関数に”因数分解“できます。
　ここで具体例を見てみましょう。2点グリーン関数と２点単連結グリーン関数の関係を求めてみると次のようになります。
$G(x_1,x_2)=G_c(x_1,x_2)$
これはファインマングラフを展開して書くと次のようにも書けます。!
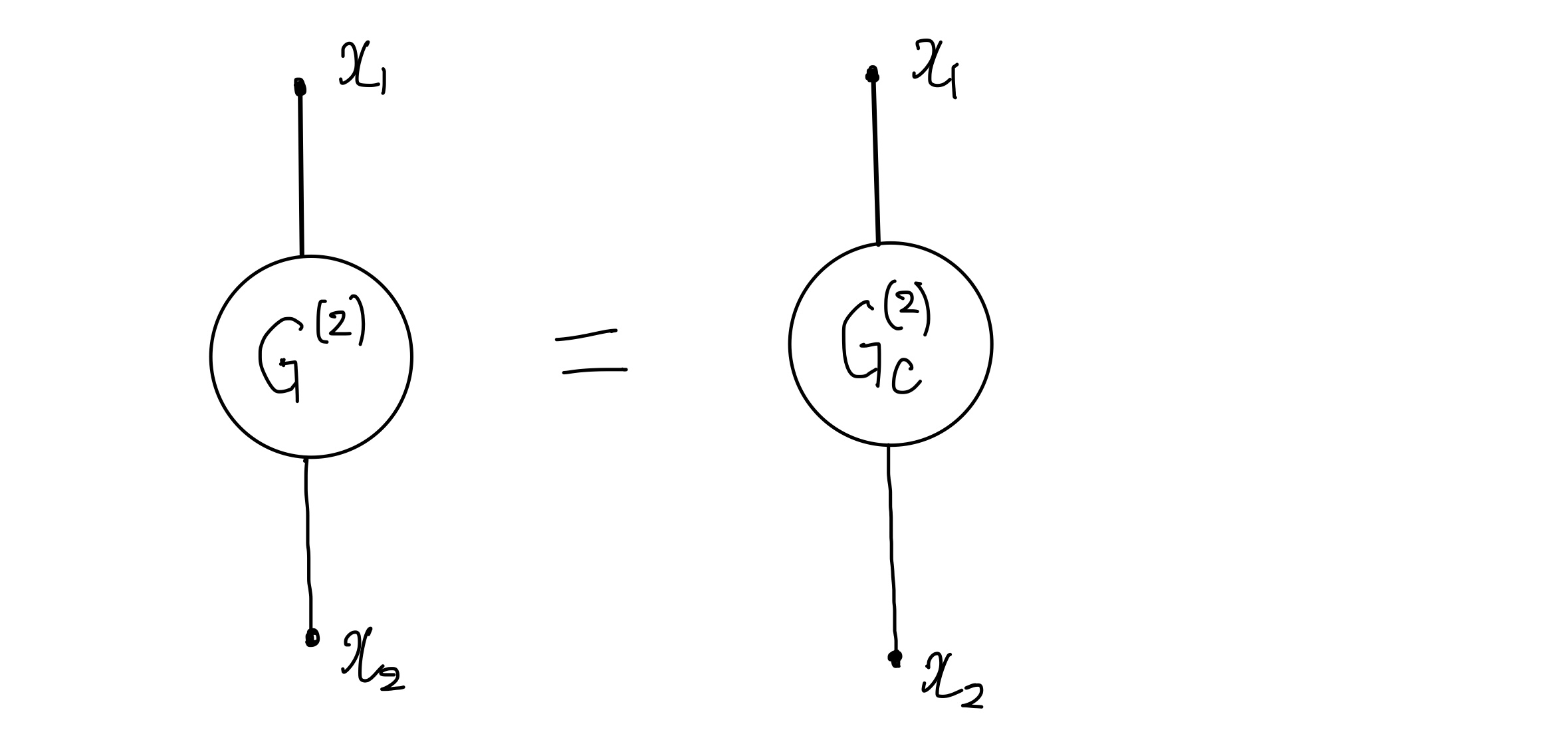グリーン関数と連結グリーン関数2次

また、4点グリーン関数については
$G(x_1,x_2,x_3,x_4)=G_c(x_1,x_2)G_c(x_3,x_4) +G_c(x_1,x_3)G_c(x_2,x_4)+G_c(x_1,x_4)G_c(x_2,x_3)+ G_c(x_1,x_2,x_3,x_4)$
これを中身を展開すると次のようになり、「因数分解」されたような形になっています。
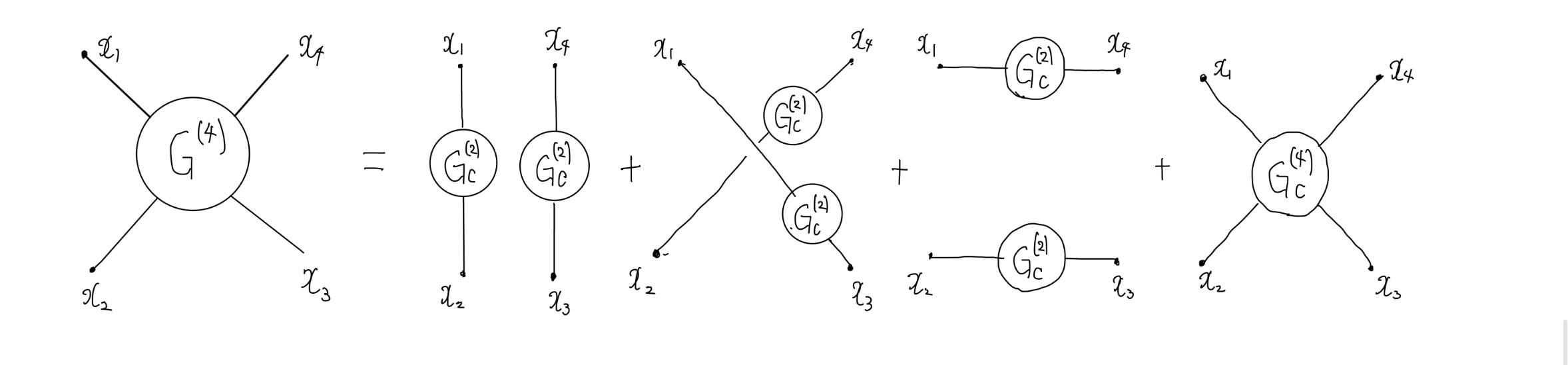グリーン関数と連結グリーン関数4次

有効作用

これでもう十分きれいにまとまった！と思うかもしれませんが、まだ分解できます。次はこの$W[J]$をルジャンドル変換することで、量子補正を加えた有効作用$\Gamma[\varphi]$を得ることができます。この汎関数は名前の通り、量子論における作用汎関数のような役目を持っています。

この汎関数はファインマングラフの構造を見るときにどのような役割を果たすのでしょうか？
実は、有効作用は一粒子規約（どの内線を切っても連結グラフになっているグラフのこと)なファインマングラフの生成汎関数になっているのです。以下でそれを証明していきます。

作用汎関数の修正

　まず、ファインマングラフを切断する操作を解析的な計算に置き換えます。そこで作用汎関数を次のように修正します。
$S_\alpha [\phi] =\displaystyle \int d^4x \bigg\{\frac{1}{2} \phi(x)[-\partial_\mu \partial^\mu-m^2+i \epsilon]\phi(x)-V(\phi)\bigg\}+\int d^4xd^4y\frac{\alpha}{2}\phi(x)\phi(y)$
かなり天下り的な操作なのですが、この先の展開を話しておくと$\Gamma$を$\alpha$で微分する操作がグラフの切断に対応するということに対応していきます。
この項を加えたことにより、この場でのプロパゲーターにも$\alpha$
による修正がかかり、それは次のようになります。
$\Delta_{\alpha}(x-y)=\displaystyle \Delta_{F,0}(x-y)+i\alpha \int d^4w \Delta_{F,0}(x-w) \int d^4w' \Delta_{F,0}(y-w') +\mathcal{O}(\alpha^2)$
そして$\alpha$の一次の項はファインマングラフを切断したものとみることができます。そのため$\frac{\partial \Gamma[\varphi]} {\partial \alpha}$ のグラフは$\Gamma$の内線を一か所切ったグラフの和になっており、これががすべて連結であることを示せばよい、ということになります。
ここで、$\alpha$に関する修正を入れた$W_\alpha[J]$が次のようになります。
$\exp(iW_{\alpha}[J])= \displaystyle\int\mathcal{D}\phi e^{i\{S_\alpha[\phi]+\int d^4zJ(z)\phi(z)\}} $

$=\displaystyle\int\mathcal{D}\phi e^{i\{S[\phi]+\int d^4zJ(z)\phi(z)\}}\exp{\bigg\{\frac{i\alpha}{2}\int d^4x\int d^4y \phi(x)\phi(y)\bigg\}} $

$ =\displaystyle\int\mathcal{D}\phi e^{i\{S[\phi]+\int d^4zJ(z)\phi(z)\}}\bigg(1+\frac{i\alpha}{2}\int d^4x\int d^4y \phi(x)\phi(y)\bigg)$

$=\displaystyle\exp(iW[J])-\frac{i\alpha}{2}\int d^4x\int d^4y \frac{\delta^2}{\delta J(x)\delta J(y)}(e^{iW[J]})$

$=\displaystyle\exp\bigg[iW[J]+i\frac{\alpha}{2} \bigg\{\bigg(\int d^4x\frac{\delta W[J]}{\delta J(x)}\bigg)^2-i\int d^4xd^4y\frac{\delta^2W[J]}{\delta J(x)\delta J(y)}\bigg\}\bigg]+\mathcal{O}(\alpha^2)$

$ \alpha$微分を計算する

準備は整ったのでα微分を実行していきます。
汎関数微分についてのchain-ruleを用いることで、次の等式を導くことができます。
$\frac{\partial \Gamma_\alpha[\varphi]}{\partial \alpha} \bigg\vert_{\varphi=固定}^{\alpha=0} =\frac{\partial W_\alpha[J]}{\partial \alpha} \bigg\vert_{J=固定}^{\alpha=0}=\displaystyle \frac{1}{2} \bigg\{\bigg(\int d^4x\frac{\delta W[J]}{\delta J(x)}\bigg)^2-i\int d^4xd^4y\frac{\delta^2W[J]}{\delta J(x)\delta J(y)}\bigg\}$
　まず一行目では$\Gamma_\alpha[\varphi]$を定義に沿って$W_\alpha[J]$に書き換えます。そしてここでの$J$は$\alpha$に依存しているので次のようになります。
$\displaystyle\frac{\partial \Gamma_\alpha[\varphi]}{\partial \alpha} \bigg\vert_{\varphi=固定}^{\alpha=0}$

$\displaystyle=\frac{\partial W_\alpha[J]}{\partial \alpha} \bigg\vert_{\varphi=固定}^{\alpha=0}- \int d^4x \frac{\partial J(x)}{\partial \alpha}\bigg\vert_{\varphi=固定}^{\alpha=0}\varphi(x)$

$=\displaystyle\frac{\partial W_\alpha[J]}{\partial \alpha} \bigg\vert_{J=固定}^{\alpha=0}+\int d^4x\frac{\delta W[J]}{\delta J(x) }\frac{\partial J(x)}{\partial \alpha}\bigg\vert_{\varphi=固定}^{\alpha=0}-\int d^4x \frac{\partial J(x)}{\partial \alpha}\bigg\vert_{\varphi=固定}^{\alpha=0}\varphi(x)$
$=\displaystyle\frac{\partial W_\alpha[J]}{\partial \alpha} \bigg\vert_{J=固定}^{\alpha=0}$

$=\displaystyle \frac{1}{2} \bigg\{\bigg(\int d^4x\frac{\delta W[J]}{\delta J(x)}\bigg)^2-i\int d^4xd^4y\frac{\delta^2W[J]}{\delta J(x)\delta J(y)}\bigg\}$
二行目については、
　そして、それぞれの項が単連結かどうかを考えていきます。まず、一項目については$S_\alpha[\phi]$に加えられた項そのものであることがわかるので、一粒子規約です。二項目についても考えてみると、$J(x)$に関する汎関数微分は、グラフを分断しないので連結グラフであることがわかります。

具体的に書いてみる

　最後に、単連結グリーン関数がどのように分解されるかを視覚的に見てみましょう。次の式は4点連結グリーン関数を一粒子規約なグラフで分解して書くと次のようになります。
4点連結グリーン関数
一般の相互作用では、上のように書き表せますが、$\Gamma^{(3)}$は$\phi^4$相互作用のみの場合0になるので、第一項のみが残ることになります。

まとめ

　今回の記事では、ファインマングラフは連結グリーン関数の生成汎関数を用いてきれいにまとめることができ、さらに連結グリーン関数は一粒子規約なグラフに分解できることを見てきました。有効作用は今回見てきた性質以外にも、重要な性質があり繰り込みを考えるときにも大事な役割を果たします。かなり過程の省略が多くなってしまいましたが、この記事で少しでもファインマングラフの面白さが伝わったらうれしいです。

修正

2025/11/4　L_0の説明、グリーン関数の図式を追加