整数解を考えるのに無理数が出てくるよ！って話

$(x,y,z)$をピタゴラス数とする。このとき、$X= \displaystyle{\frac{x}{z}},Y=\displaystyle{\frac{y}{z}}$とおくと
$$ \begin{eqnarray} x^2+y^2=z^2 &\Longleftrightarrow& \left(\frac{x}{z}\right)^2+\left(\frac{y}{z}\right)^2=1 \\ &\Longleftrightarrow& X^2+Y^2=1\\ \end{eqnarray}$$
となり、$X,Y$は有理数であるので単位円上の有理点を考えれば良いとわかり、$x,y,z$が正の整数であることから単位円上の第１象限にある有理点のみを考えれば良いことがわかる（ただし２点$(1,0)$,$(0,1)$を除く）。
ここで点$(-1,0)$を通り、傾きが$0< m<1$であるような直線を考える。
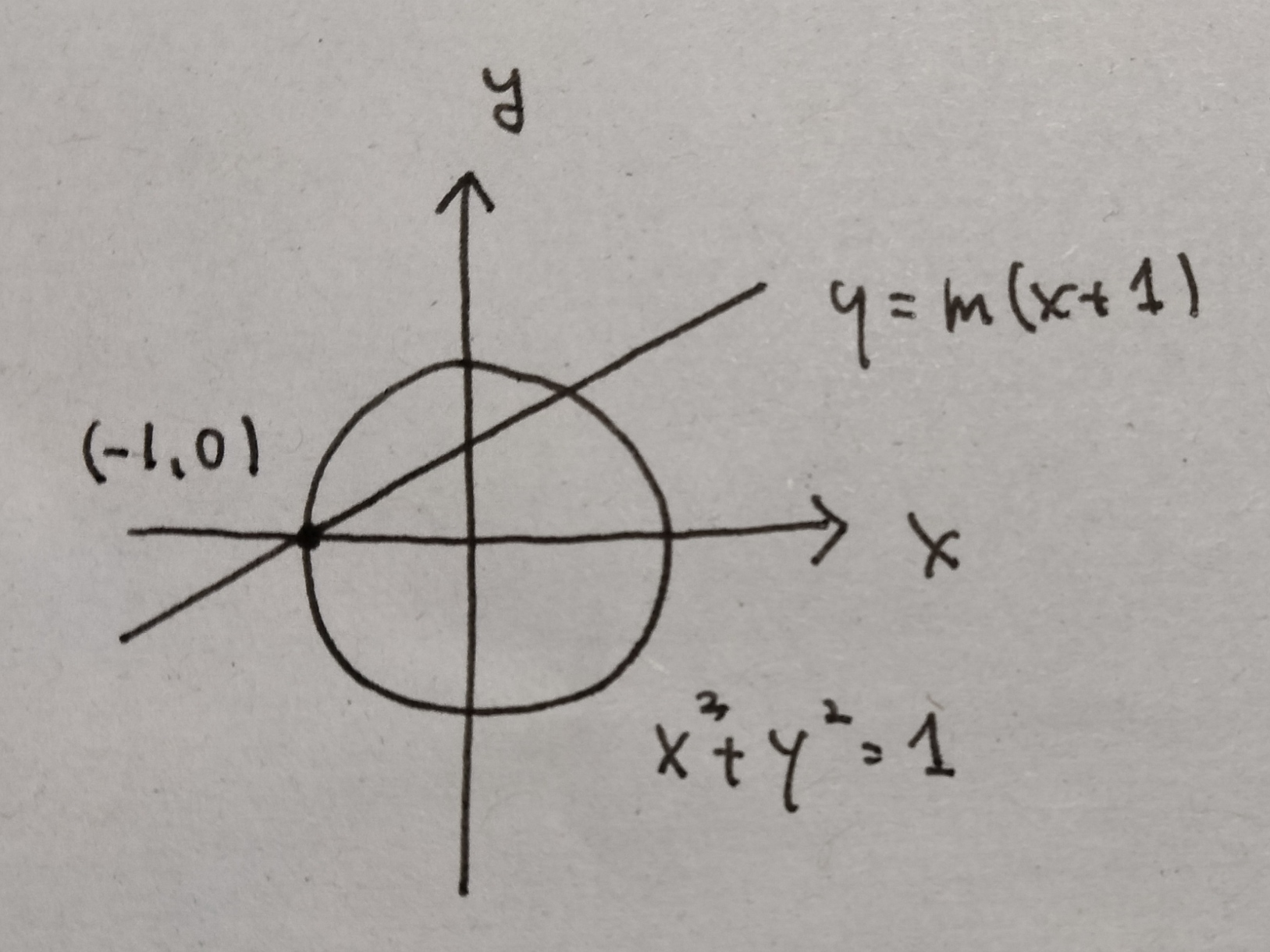単位円と直線
図１よりこの直線と単位円が点$(-1,0)$と第１象限にてもう１点で交わることがわかるのでその交点の座標を調べる。直線の方程式$Y=m(X+1)$を$X^2+Y^2=1$に代入すると
$$ \begin{eqnarray} &X^2+(m(X+1))^2& = 1 \\ &X^2+m^2(X^2+2X+1)& = 1 \\ &(m^2+1)X^2+2m^2X+(m^2-1)& = 0 \end{eqnarray}$$
ここで、図１より$X=-1$が解であるので因数定理から
$$ (X+1)((m^2+1)X+(m^2-1))=0$$
のように変形できるので$X=-1,\displaystyle{\frac{1-m^2}{1+m^2}}$が得られる。$X=\displaystyle{\frac{1-m^2}{1+m^2}}$を$Y=m(X+1)$に代入すると$Y=\displaystyle{\frac{2m}{1+m^2}}$となる。よって、求めたかった交点の座標は$\left(\displaystyle{\frac{1-m^2}{1+m^2}},\displaystyle{\frac{2m}{1+m^2}}\right)$となるが$m$が有理数のとき、交点は有理点となることがわかる。ゆえに$(X,Y)=\left(\displaystyle{\frac{1-m^2}{1+m^2}},\displaystyle{\frac{2m}{1+m^2}}\right)$が式$X^2+Y^2=1$の有理数解となることがわかる。
逆に$(X_1,Y_1)$を単位円上の有理数点とすると、2点$(-1,0),(X_1,Y_1)$を通る直線の傾き$m$は有理数となる。
よって、単位円上の第１象限にある有理数点は$0< m<1$を有理数とすると$(X,Y)=\left(\displaystyle{\frac{1-m^2}{1+m^2}},\displaystyle{\frac{2m}{1+m^2}}\right)$ですべて与えられる。$0< m<1$は有理数であるので$0< v< u$を整数とすると$m=\displaystyle\frac{v}{u}$とおけ、これを用いると
$$ \begin{eqnarray} (X,Y) &=& \left({\frac{1-m^2}{1+m^2}},{\frac{2m}{1+m^2}}\right) \\ &=& \left({\frac{u^2-v^2}{u^2+v^2}},{\frac{2uv}{u^2+v^2}}\right) \\ \left(\frac{x}{z},\frac{y}{z}\right) &=& \left({\frac{u^2-v^2}{u^2+v^2}},{\frac{2uv}{u^2+v^2}}\right) \\ (x,y,z) &=& (u^2-v^2,2uv,u^2+v^2) \end{eqnarray}$$
よって題意は示された。

$Y$を任意の正の整数とする。このとき$Y+1$個の数
$0 \cdot \alpha=N_0+F_0$ ,$N_0=0$ ,$F_0=0 $
$1 \cdot \alpha=N_1+F_1$ ,$N_1 \in \mathbb{Z}$ ,$0 \leq F_1<1$
$2 \cdot \alpha=N_2+F_2$ ,$N_2 \in \mathbb{Z}$ ,$0 \leq F_2<1$
$\cdots$
$Y \cdot \alpha=N_Y+F_Y$ ,$N_Y \in \mathbb{Z}$ ,$0 \leq F_Y<1$
と、$Y$個の区間
$$ \left[\frac{0}{Y},\frac{1}{Y}\right),\left[\frac{1}{Y},\frac{2}{Y}\right),...,\left[\frac{Y-1}{Y},\frac{Y}{Y}\right) $$
を考える。このとき$F_i (i=0,1,\cdots,Y)$を鳩、$\displaystyle{\left[ \frac{i-1}{Y},\frac{i}{Y}\right)}(i=1,\cdots,Y)$を巣として鳩ノ巣原理を適用すると、ある正の整数$n,m(0 \leq m< n \leq Y)$が存在して
$$ |F_m-F_n|< \frac{1}{Y}$$
が成立することがわかる（$Y+1$匹いる鳩を$Y$個の巣に押し込めているので少なくとも１つの巣は２匹の鳩をもつ）。
ここで関係式$m\alpha=N_m+F_m$,$n\alpha=N_n+F_n$と置換$x=N_n-N_m$,$y=n-m$を用いると上式は
$$ \begin{eqnarray} |(N_n-N_m)-(n-m)\alpha|& < \frac{1}{Y}\\ |x-y\alpha| < \frac{1}{Y} \end{eqnarray}$$
とかける。よって任意の正の整数$Y$に対して$|x-y\alpha|<\displaystyle \frac{1}{Y}$をみたす正の整数$x,y$が存在することがわかる。(正直な話なんでxが正になるのかがわかってません、わかる方がいたら教えてくれると助かります)
このことから$Y$をさらに大きくとると$|x-y\alpha|<\displaystyle \frac{1}{Y}$をみたす正の整数$x,y$が新たに得られ$0< y \leq Y$に注意すると、これを繰り返すことで不等式$|x-y\alpha|<\displaystyle \frac{1}{y}$をみたす正の整数の組$(x,y)$が無数に存在することがわかる。

正の整数の組$(x,y)$が$|x-y\sqrt{D}|<\displaystyle \frac{1}{y}$を満たしているとする。
ここで、$x< y\sqrt{D}+\displaystyle \frac{1}{y}$が成り立つので
$$ \begin{eqnarray} x+y\sqrt{D} &<& (y\sqrt{D}+\frac{1}{y})+y\sqrt{D}\\ &\leq& 3y\sqrt{D} \end{eqnarray}$$
上式の両辺に$|x-y\sqrt{D}|$をかければ
$$ \begin{eqnarray} |x^2-Dy^2| &<& 3y\sqrt{D}\cdot|x-y\sqrt{D}|\\ &<& 3y\sqrt{D}\cdot\frac{1}{y}\\ &=& 3\sqrt{D} \end{eqnarray}$$
以上より、$|x-y\sqrt{D}|<\displaystyle \frac{1}{y}$をみたす正の整数の組$(x,y)$は
$|x^2-Dy^2|<3\sqrt{D}$を満たす。
ここで、$T=\lfloor3\sqrt{D}\rfloor$とおく（$\lfloor \quad \rfloor$はガウス記号）。
鳩として$|x-y\sqrt{D}|<\displaystyle \frac{1}{y}$を満たす正の整数$(x,y)$を、巣として整数
$$ -T,-T+1,\cdots,-1,1,\cdots,T-1,T$$
をとる。今、補題３より$|x-y\sqrt{D}|<\displaystyle \frac{1}{y}$をみたす正の整数の組$(x,y)$が無数にあることに注意して鳩ノ巣原理を用いると
$(x,y)$が鳩のとき、式$x^2-Dy^2$は$-T$から$T$の間にあるので明らかにある整数$M(-T\leq M \leq T,M \neq 0)$が存在して、$x^2-Dy^2=M$は無数の正の整数解$(x,y)$をもつ（無限匹いる鳩を$2T$個の巣に押し込めているので少なくとも１つの巣は無限匹の鳩をもつ）。
$x^2-Dy^2=M$の正の整数解を$(X_i,Y_i),(i=1,2,\cdots)$で表す。
以下、$M$を法として
$$ X_j\equiv X_k \qquad Y_j\equiv Y_k$$
を満たす整数解を鳩ノ巣原理を使って探す。
鳩として$(X_i,Y_i)$を、巣として$(A,B),(0\leq A,B< M)$を設定し、各鳩$(X_i,Y_i)$を巣に入れるのにそれぞれの$M$で割った余りを考える。すると再び鳩ノ巣原理より、
$$ \begin{eqnarray} X_j \equiv X_k \qquad X^2_j-DY^2_j=M\\ Y_j \equiv Y_k \qquad X^2_k-DY^2_k=M \end{eqnarray}$$
をみたす$(X_j,Y_j),(X_k,Y_k)$が存在することがわかる（無限匹いる鳩を$M^2 $個の巣に押し込めているので少なくとも１つの巣は無限匹、つまり２匹以上の鳩をもつ）。そして実は
$$ x=\frac{X_jX_k-Y_jY_kD}{M}\qquad y=\frac{X_jY_k-X_kY_j}{M}$$
がペル方程式$x^2-Dy^2=1$の整数解となっている。実際に、
$$ \begin{eqnarray} x^2-Dy^2 &=& \left(\frac{X_jX_k-Y_jY_kD}{M}\right)^2-D\left(\frac{X_jY_k-X_kY_j}{M}\right)^2\\ &=& \frac{(X_j^2-DY_j^2)(X_k^2-DY_k^2)}{M^2}\\ &=& 1 \end{eqnarray}$$
であり、後は$x,y$が共に整数であることを示せばよい。それには$x,y$の分子が共に$M$の倍数であることが言えればよいが、
$$ \begin{eqnarray} &X_jX_k-Y_jY_kD& \equiv X_j^2-Y_j^2D=M \equiv 0 \\ &X_jY_k-X_kY_j& \equiv X_jY_j-X_jY_j \equiv 0 \end{eqnarray}$$
これより$x,y$が共に整数であることがわかり、必要があれば負の符号を置き換えることで整数解$(x,y)$,$(x,y \geq 0)$が存在することがわかる。そして今、
$$ \begin{eqnarray} 0 &\leq& y \\ 0 &\leq& Dy^2\\ 1 &\leq& Dy^2+1=x^2 \end{eqnarray}$$
となるので$x \geq 1$となる。ここで$y=0$と仮定すると$y^2=\displaystyle\frac{x^2+1}{D}$であるので$x^2=-1$となり、$x \geq 1$に矛盾することから$y \geq 1$がわかる。以上のことから$(x,y)=\left(\displaystyle\frac{X_jX_k-Y_jY_kD}{M},\frac{X_jY_k-X_kY_jD}{M}\right)$がペル方程式$x^2-Dy^2=1$の正の整数解であることが示された。