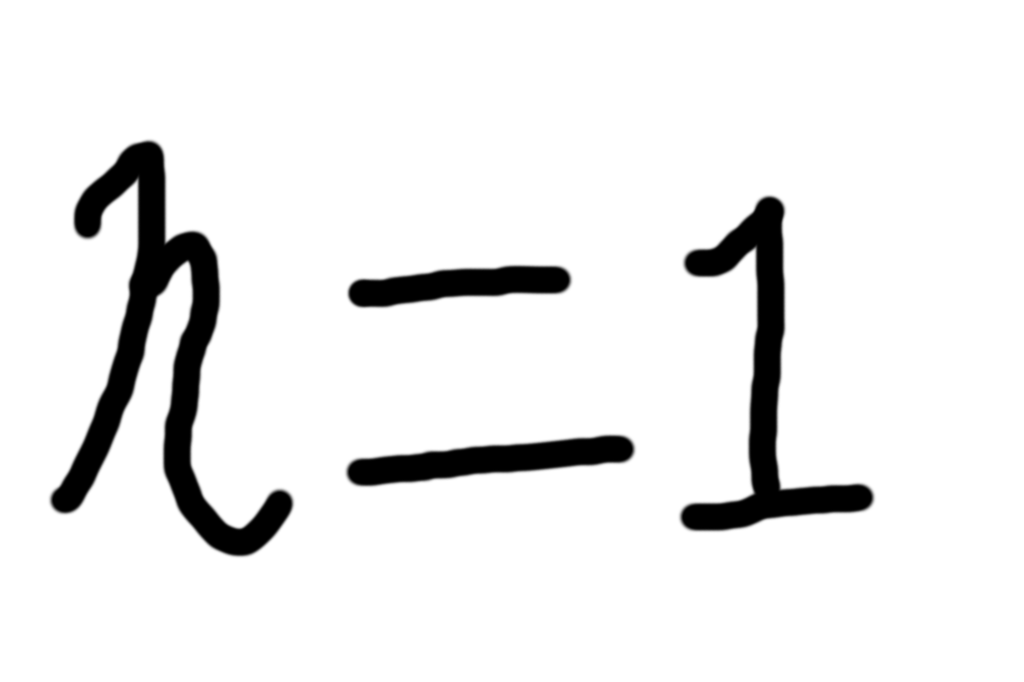√して負の数2

はじめに

　こんにちは、最近漸化式ガチャにはまっているn=1です。今回は この記事 の続きについてやっていきます。

定義

　 前回 と同じで、$\sqrt{x}=-1$となる$x$を$s$とします。また、$\sqrt 1\ne -1$なので当然$s\ne 1$です。

矛盾点について

　前回は、$\sqrt{x}^2=y\neq x$として$\sqrt{s}^2=1 \Longleftrightarrow s=1$を回避していました。しかし、今回私が考えたものは当然$(-1)^2=1$となり、また定義より$(-1)^2=s$ともなるという$(-1)^2=1,s$という別解がうまれることから起きた間違いから起きてしまったのではないかという考えです。
　$(-1)^2=1,s$だから
$\sqrt{s}^2=\sqrt{(-1)^2}^2=\sqrt1 ^2=1$
$　　　　　　　　　=\sqrt s ^2=s$
そのため$\sqrt{s}^2=1,s$とします。なお、これによりどちらにせよ$\sqrt{x}^2=y\neq x$という別解がうまれるということは変わっていませんし、おそらく指数の$(x^m)^n=x^{mn}$とは限らないです。

性質

　性質としては前回あったように、
$\frac{1}{s}=s$
なので
$\frac{s}{s}=s^2=1$
となり、 分解型複素数 のような性質を持っています。
　四則演算は、分解型複素数のような性質を持っているので、以下のようになります。
$(a+bs)+(c+ds)=(a+c)+(b+d)s$
$(a+bs)-(c+ds)=(a-c)+(b-d)s$
$(a+bs)(c+ds)=(ac+bd)+(ad+bc)s$
$\frac{a+bs}{c+ds}=\frac{ac+bd}{c^2-d^2}+\frac{ad+bc}{c^2-d^2}s$
そして除法から$1 \pm s$は 零因子 になります。

応用

　応用として、この数を使い偶数乗根の解が負になるものを求めると
$\sqrt{x}=-1 \Longleftrightarrow x=s$
$\sqrt[4]{x}=-1 \Longleftrightarrow x=s^2=1$
しかし、当然$\sqrt[4]{1}\ne-1$なので、4乗根以降はまた新たな数を考えなければいけません。
　なお、$\sqrt{1+s}=\pm\frac{1+s}{\sqrt2},\sqrt{1-s}=\pm\frac{1-s}{\sqrt2}$となりますが、他の場合の√は解が4つになります。

最後に

　記事を書いてて応用の4乗根以降ができないのは指数が有理数の場合は分数から計算すれば避けられそうだなと思いました。
　以上で√して負の数は終わりです。間違っている部分があると思うのであったらご指摘お願いします。投稿を見てくださりありがとうございました。