テルドラゴン曲線を描く
テルドラゴン曲線というのがある。次のように作る。
方向列を$[0]$からスタートして次のように作っていく。
$$[a_0,a_1,\cdots ,a_{n-1}]\to[a_0,a_1,\cdots ,a_{n-1},a_0+1,a_1+1,\cdots,a_{n-1}+1,a_0,a_1,\cdots,a_{n-1}]$$
成分は$0,1,2$でモジュロ$3$の足し算とする。ひとつひとつは$120$°回転に対応している。このやり方で作っていく曲線のことをいう。こんな感じ：
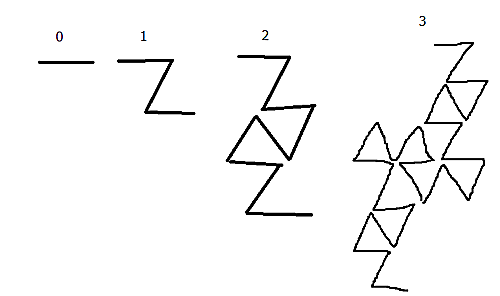テルドラゴン1
回転方向は時計回りとする。
$$[0]\to[0,1,0]\to[0,1,0,1,2,1,0,1,0]\to \cdots$$
作っていくとこんな感じになる。
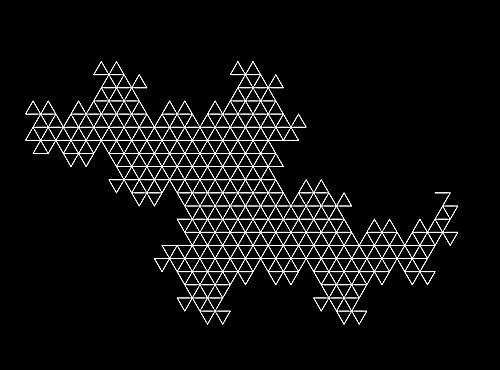テルドラゴン2
この曲線の$n$回目の進行方向を考えてみる（$0$回目は$0,~1$回目は$1,\cdots$）。まず、方向列の作り方が、
$$[\alpha]\to[\alpha,~\alpha+1,~\alpha]$$
となっている。この$3$つの区分は$n$を$3$進数展開したときの最上位桁$0,1,2$に対応しているので、それが$1$の場合だけ真ん中に入る。そして$1$を引いて続きは$\alpha$の中で同じことをする。それは頭の桁を取り去ることに対応するから、結局桁が$1$のときだけ実際の値から$1$を引いて残りを調べる形になる。最後は$[0,1,0]$だから末尾も$1$のときだけ$1$になってて最後は$0$になる。ゆえに、$1$の数だけ$120$°回転すれば$n$での進行方向が出る。
テルドラゴン曲線の第$n$番目の進行方向は、$n$を$3$進数展開したときに桁に現れる$1$の個数だけ$120$°回転した方向。
最初のいくつかの数字を$3$進数展開して並べてみる：
$$0,~1,~2,~10,~11,~12,~20,~21,~22,~100,~101,~102,~110,~111,~112,~120,~121,~\cdots$$
確かに$1$の個数で回転角が決まっていることが分かる。
実際にこれをp5.jsで作成するコードを置いておく。
作品ページ
let a = 0;
let b = 0;
let f = 0;
function setup(){
createCanvas(600, 600);
stroke(255);
background(0);
}
function draw(){
translate(540, 300);
let u = f;
let x = 0;
while(u){
x += (u % 3) & 1;
u = (u - (u % 3)) / 3;
}
let c = 20 * cos(x * 2 * PI / 3);
let s = 20 * sin(x * 2 * PI / 3);
line(a, b, a + c, b + s);
a += c;
b += s;
f++;
}
$f$が項数で、$u$に代入して計算しているところで使っている。$x$が$1$の個数。下から見ていく。$0,1,2$のうち&を取って$1$になるのは$1$だけだからビット演算で出る。$1$の個数に$2\pi/3$を掛けると進行方向が出る。そんな感じ。
6つの方向に出してみる
テルドラゴン曲線は6つの方向に伸ばしていくと正三角形格子のすべての辺を一つ残らずなぞることが知られている。それを実行したコードがこれ：
作品ページ
テルドラゴン3
let a = 0;
let b = 0;
let f = 0;
function setup(){
createCanvas(600, 600);
colorMode(HSB, 100);
background(0);
}
function draw(){
translate(300, 300);
let u = f;
let x = 0;
while(u){
x += (u % 3) & 1;
u = (u - (u % 3)) / 3;
}
let c = 9 * cos(x * 2 * PI / 3);
let s = 9 * sin(x * 2 * PI / 3);
let r = 6;
while(r--){
rotate(PI / 3);
let v = r % 2;
stroke(55, 100 * v, 100);
line(a, b, a + c, b + s);
}
a += c;
b += s;
f++;
}
すべての辺をちょうど1回ずつ通るので、そこにひし形を配置して平面充填することができる。それを実行するとこんな感じになる：
作品ページ
テルドラゴン4
const SIZE = 640;
const HALF_SIZE = SIZE / 2;
let x = 0;
let y = 0;
let properFrameCount = 0;
const k = Math.PI / 3;
const UNIT_LENGTH = 6;
const SHORT_LENGTH = UNIT_LENGTH / Math.sqrt(3);
let gr;
function setup(){
createCanvas(SIZE, SIZE);
gr = createGraphics(SIZE, SIZE);
gr.colorMode(HSB, 96);
gr.noStroke();
gr.translate(HALF_SIZE, HALF_SIZE);
}
function draw(){
background(128);
let rp = 20;
while(rp--){
let u = properFrameCount;
let z = 0;
while(u){
z += 2 * ((u % 3) & 1);
u = (u - (u % 3)) / 3;
}
let s = UNIT_LENGTH * cos(z * k);
let t = UNIT_LENGTH * sin(z * k);
let s1 = SHORT_LENGTH * cos(z * k - PI / 6);
let t1 = SHORT_LENGTH * sin(z * k - PI / 6);
let s2 = SHORT_LENGTH * cos(z * k + PI / 6);
let t2 = SHORT_LENGTH * sin(z * k + PI / 6);
let r = 6;
const sat = properFrameCount % 50 + 50;
const blt = properFrameCount % 40 + 60;
while(r--){
gr.rotate(k);
gr.fill(r * 16, sat, blt);
gr.quad(x, y, x + s1, y + t1, x + s, y + t, x + s2, y + t2);
}
x += s;
y += t;
properFrameCount++;
}
image(gr, 0, 0);
if(properFrameCount > 14000){ noLoop(); }
}
すべての格子の辺を1回ずつ通るのについてはそのうち証明してみたいと思う。ドラゴン曲線の方も（正方形格子）。あっちはなんとか証明できそうなのでそのうち上げたい。
