平行な2直線間の距離
初めまして、しょぼんと申します. 平行な2直線間の距離を求めてみたいと思います.
 3
3
必要知識
知識は点と直線の距離の公式(下)のみです.
直線$ax+by+c=0$と点$(x_0, y_0)$との距離$D$は$\displaystyle D=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$
高校数学で重要なこの定理を使います.
問題
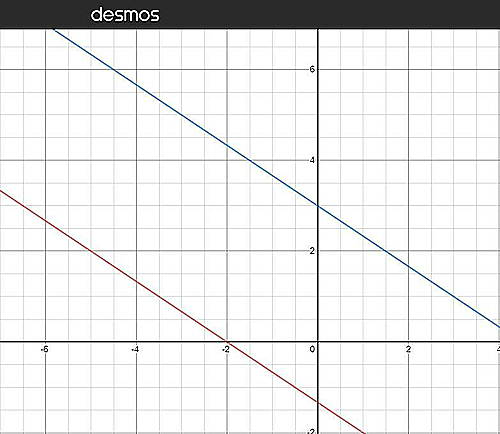
平行な$2$直線$2x+3y+4=0, 2x+3y-9=0$の距離を求めよ.
答えは$13$ではありません.
発想
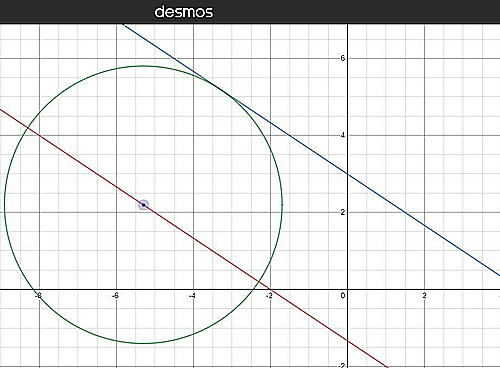
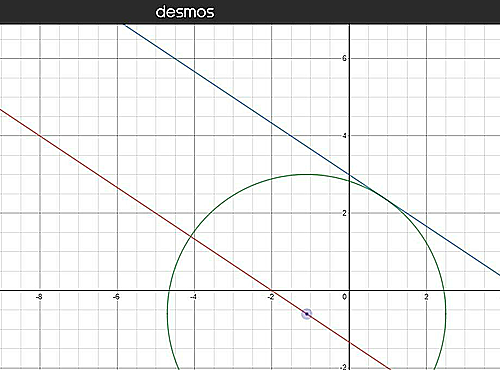
$(x_0, y_0)$は$2x+3y+4=0$上の点とします. このとき, どの点をとったとしても, その点ともう一方の直線の距離は変わりません.
 1
1
 2
2
上の2つの画像の円の半径(=距離)は同じです.
解答
$(-2,0)$は, 直線$2x+3y+4=0$上の点である. $(-2,0)$と$2x+3y-9=0$との距離は$\displaystyle \frac{|-4-9|}{\sqrt{2^2+3^2}}=\frac{13}{\sqrt{13}}=\sqrt{13}$
$2x+3y+4=0$上の点と$2x+3y-9=0$との距離は, 一定である.
よって, 平行な$2$直線$2x+3y+4=0, 2x+3y-9=0$の距離は$\mathbf{\sqrt{13}}$である.
拡張
いろいろ拡張してみます
平行な2直線の距離の公式
平行な2直線$ax+by+c=0, ax+by+d=0$の距離を求めます. 発想と同様に考えて,
$ax+by+d=0$上に点$(x_0, y_0)$をとる. このとき, $ax_0+by_0+d=0\cdots\text{(A)}$が成り立ちます.
$(x_0, y_0)$と$ax+by+c=0$との距離$D$は, $\displaystyle D=\frac{|ax_0+by_0+c|}{a^2+b^2}$です.
ここで$\text{(A)}$より, $ax_0+by_0=-d$であるので, $\displaystyle D=\frac{|c-d|}{\sqrt{a^2+b^2}}$
平行な2直線$ax+by+c=0, ax+by+d=0$の距離$D$は$\displaystyle D=\frac{|c-d|}{\sqrt{a^2+b^2}}$
平行な2平面の距離
前提となる次の定理を紹介します. 証明は, 数Bのベクトルを導入します.
平面$ax+by+cz+d=0$と点$(x_0, y_0, z_0)$との距離$D$は$\displaystyle D=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$
そのまま3変数に拡張したような感じですね!本題には関係ないですが, 比較的マイナーな定理なので証明をします.
証明は, 次の補題を使います.
$(a, b, c)$は平面$ax+by+cz+d=0$に垂直なベクトルである.
$ax+by+cz+d=0$上に異なる点$P, Q$をとり, その位置ベクトルを$\overrightarrow{p}, \overrightarrow{q}$とする.
ここで, Oを原点とおき, $\overrightarrow{p}=(x_0, y_0, z_0), \overrightarrow{q}=(x_1, y_1, z_1)$とする. このとき$ax_0+by_0+cz_0=-d$かつ$ax_1+by_1+cz_1=-d$である.
さて, $(a,b,c)\cdot \overrightarrow{u}=(a,b,c)\cdot(\overrightarrow{p}-\overrightarrow{q})=a(x_1-x_0)+b(y_1-y_0)+c(y_1-z_0)=-d+d=0.$ よって, あらゆる$ax+by+cz+d=0$上の点$P,Q$について $(a,b,c)\perp PQ$であるので, $(a,b,c)\perp $[$ax+by+cz+d=0$が表す平面].
これを用いて定理3を証明します.
点$(x_0, y_0, z_0)$から平面$ax+by+cz+d=0$に垂線をひき, その垂線と平面との交点を$A(p, q, r)$とする.その垂線のベクトルは, $(a,b,c)$である($\because$ 補題4)から, 実数$k$を用いてOを原点とおいたベクトル方程式 $(x_0,y_0,z_0)+k(a,b,c)=(p,q,r)$が成り立つ. $k(a,b,c)=(p-x_0, q-y_0, r-z_0)\cdots\text{(A)}$となる.
ここで$A(p,q,r)$は$ax+by+cz+d=0$上の点なので, $ap+bq+cr+d=0\cdots\text{(B)}$.
$\text{(A)}$の左辺と$(a,b,c)$との内積をとると, $k(a,b,c)\cdot(a,b,c)=k(a^2+b^2+c^2)$.
一方 $\text{(A)}$の右辺と$(a,b,c)$との内積をとると, $(p-x_0, q-y_0, r-z_0)\cdot(a,b,c)=ap+bq+cr-ax_0-by_0-cz_0=-ax_0-by_0-cz_0-d$.
よって, $\displaystyle k(a^2+b^2+c^2)=-ax_0-by_0-cz_0-d \therefore k=\frac{-ax_0-by_0-cz_0-d}{a^2+b^2+c^2}$
さて, $(x_0, y_0, z_0)$と平面$ax+by+cz+d=0$の距離$D$は$|k(a,b,c)|$と等しい. よって,
$\displaystyle D=|k||(a,b,c)|=\left|\frac{-ax_0-by_0-cz_0-d}{a^2+b^2+c^2}\right|\sqrt{a^2+b^2+c^2}=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$
さて, 平行な2平面間の距離の公式を出します. といっても, 予想はついていると思うので先に結果をだします.
平行な2平面$ax+by+cz+d=0, ax+by+cz+e=0$の距離$D$は$\displaystyle D=\frac{|d-e|}{\sqrt{a^2+b^2+c^2}}$
発想と同様に考えて,
$ax+by+cz+e=0$上に点$(x_0, y_0, z_0)$をとる. このとき, $ax_0+by_0+cz_0+e=0\cdots\text{(A)}$が成り立つ.
$(x_0, y_0, z_0)$と$ax+by+cz+d=0$との距離$D$は, $\displaystyle D=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$($\because$定理3)
ここで$\text{(A)}$より, $ax_0+by_0+cz_0=-e$であるので, $\displaystyle D=\frac{|d-e|}{\sqrt{a^2+b^2+c^2}}$
