複素座標入門1/5 複素座標って?
どうもnatuです.第0回は見ていただけたでしょうか.第1回では「基本的なこと」を書きます.数Ⅲの学習が済んでいる人はさらっと流してもらって構いません.では行こう!
基本的なこと
複素座標は平面上の点を複素平面上の複素数に対応させる考え方です.直交座標平面上の点$(x,y)$を一つの数$x+yi$として扱おうということです.このとき$x$を実部,$y$を虚部といいます.しかし実際に2つの文字を使うことはなかなかありません.普通は1つの複素数を$z$で表します.
また,この記事では特に断らない限り大文字で表された点$X$に対応する複素数を単純に小文字で$x$で表すことにします.
複素数を扱うときに特に留意しておきたいのは複素数は位置ベクトルであるということです.例えば線分$AB$の長さは$|b-a|$で表されます.また,後述する円の方程式$|z-a|=r$は円のベクトル方程式と全く同じです .このように複素数はベクトルと同じように点と数を結びつけていると解釈できます.じゃあこれを図形問題に使おうというのが複素座標のモチベーションとなっているのです.
複素座標平面
図形を書くキャンパスとなるのは複素座標平面です.これはおなじみの実数の数直線を縦にも広げたものです.縦にどれだけかのパラメータは虚数単位$i$を用います.
このとき,初めの実数の数直線を"実軸"といい,これに垂直で,原点を通る直線を"虚軸"といいます.
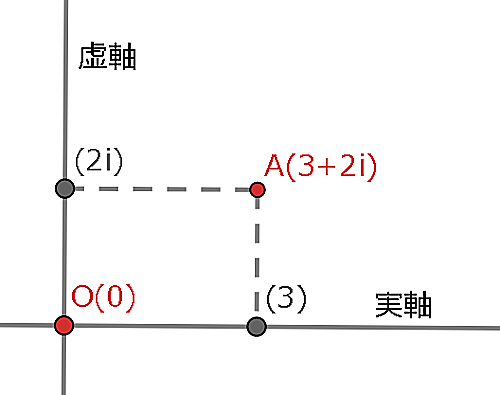
この平面上で例えば,$a=3+2i$はどの点を表すでしょうか.答えは原点から右に$3$,上に$2$だけ動いた点ですね.この点を$A$としたとき,この記事では"点$A$と複素数$a$は対応する."という言い回しをします.またこのことを"点$A$の座標は$a$である".という言い方もします.これを短く表すときは単に$A(a)$と表します.
このとき,実軸上の点に対応する複素数を"実数",虚軸上の点に対応する複素数を"純虚数"といいます.$3+2i$は実数でも純虚数でもありませんね.
また,複素数$z$の実数パラメータ,虚数パラメータの部分をそれぞれ$z$の"実部","虚部"といい,それぞれ$Re(z),Im(z)$と表します.$a=3+2i$のときは$Re(a)=3,Im(a)=2$です.当たり前ですが,任意の複素数$z$に対して,$z=Re(z)+Im(z)i$が成り立ちます.
 図
図
共役複素数
複素数$z=Re(z)+Im(z)i$に対して$Re(z)-Im(z)i$を$z$の共役複素数といい,$\overline{z}$で表します.
このとき,次のことが成り立ちます.
任意の複素数$a,b$に対して次のことが成り立つ.
$\overline{a\pm b}=\overline{a}\pm\overline{b} \overline{ab}=\overline{a}\overline{b}$
証明は練習問題とします.簡単なので.また,$z$の実部$Re(z)$,虚部$Im(z)$,絶対値$|z|$,実数である条件,純虚数である条件は次のように表せます.
$\displaystyle Re(z)= \frac{1}{2}(z+\overline{z}) Im(z)=\frac{1}{2i}(z-\overline{z}) |z|= \sqrt{z\overline{z}}$
$z$が実数$ \Longleftrightarrow z=\overline{z} z$が純虚数$ \Longleftrightarrow z+\overline{z}=0$
$z$が実数である条件は結構大事ですね.これも証明は簡単です.
直線
直交座標での直線$ax+by+c=0$を複素平面に対応させましょう.先ほど直交座標での$x,y$座標は複素平面での実部,虚部に対応するという話をしましたね.ということで$x$を$Re(z)$に,$y$を$Im(z)$にしてさらに命題2の式を代入しちゃいましょう.すると,
$\displaystyle ax+by+c=0 \Longleftrightarrow \frac{a+bi}{2}z+ \frac{a-bi}{2}\overline{z}=-c$
が得られます.なんちゃら$z$+なんちゃら$\overline{z}$=なんちゃら で直線の方程式になるということですね.もう一度$a,b,c$を用いて命題にします.
$a,b,c$を複素数とするとき方程式$az+b\overline{z}=c$は直線を表す.
実はこの命題の立て方はとても危ないです.
例えば方程式$z+\overline{z}=2$は直線$x=1$を表しますが(解が無数にあるので),
方程式$z+(1+i)\overline{z}=1$は点$(1,0)$を表すだけですし(解が1つしかないので),
方程式$z+\overline{z}=i$は何も表してくれません(解がないので)!
これは2元1次連立方程式の解の個数が0,1,無数のいずれかであることに起因しますがそのことについては入門ということで無視します.
以下,直線$az+b\overline{z}=c$などと書いているときはこの方程式が直線を表してくれていることは暗黙の了解とします.
特に,次のような直線は問題を解くうえでよく登場します.
2点$A,B$があるとき,
直線$A,B$の方程式は $(\overline{a}-\overline{b})z-(a-b)\overline{z}=\overline{a}b-a\overline{b}$
線分$A,B$の垂直二等分線の方程式は $(\overline{a}-\overline{b})z+(a-b)\overline{z}=|a|^2-|b|^2$
この命題の証明も練習問題とします.ところでこの2式,左辺が似てますね…詳しくは次回!
円
今度は円です.これも直交座標での方程式$x^2+y^2+mx+ny+l=0$に命題1の式を代入!!
といきたいところですが…面倒ですね.もちろんこのくらい代入して計算するだけの思い切りがないと先が思いやられるのですが.どうにか計算量を減らしたいと思うことも大事です.
ではどうするか,円の定義に従えばいいのです.点$A$が中心で半径が$r$の円周上の点$Z$は次の式を満たします.
$|z-a|=r$
左辺は$Z$と$A$の距離,右辺は円の半径を表しているので当たり前ですね! 別の表現をしたいならば先ほどの式の両辺を2乗して,
$r^2=|z-a|^2=(z-a)(\overline{z-a})=(z-a)(\overline{z}-\overline{a})$
$=z\overline{z}+a\overline{a}-(\overline{a}z+a\overline{z})=|z|^2+|a|^2-(\overline{a}z+a\overline{z})$
としてもよいですね.
$a$を複素数,$r$を非負実数とするとき方程式$|z-a|=r$すなわち
$|z|^2-(\overline{a}z+a\overline{z})+|a|^2=r^2$は$a$を中心とした半径$r$の円を表す.
しかし見てわかるように式が複雑なのであまりぽんぽん使いたいものではありません.使うのは$a=0$(中心が原点),$r=1$(半径が$1$)のときの$|z|=1$が多いです.この円を舞台に様々なことをすることができます.詳しくは第3,4回をご覧ください.
ところで円を決定する方法として,他には「通る3点を決める」があります.これは第4回に円の方程式2として扱います.
内分点
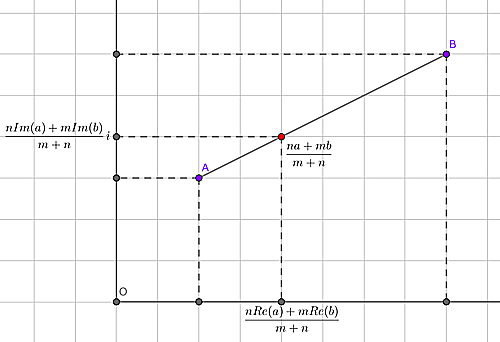
線分$AB$を$m:n$に内分する点$P$の座標を求めましょう.といっても直交座標での考え方を複素座標に輸入するだけです.すなわち実部と虚部に分けて考えると
$\displaystyle Re(p)=\frac{nRe(a)+mRe(b)}{m+n},Im(p)=\frac{nIm(a)+mIm(b)}{m+n}$ということなので$p=Re(p)+Im(p)i=\displaystyle\frac{nRe(a)+mRe(b)}{m+n}+\frac{nIm(a)+mIm(b)}{m+n}i$
$=\displaystyle\frac{n(Re(a)+Im(a)i)+m(Re(b)+Im(b)i)}{m+n}=\frac{na+mb}{m+n}$ですね.
線分$AB$を$m:n$に内分する点の座標は$\displaystyle\frac{na+mb}{m+n}$
外分は本質的には内分と同じ(内分比を負の数に拡張しただけ)なので特に命題にはしません.
 図
図
練習問題
level1
次の命題を示せ.
(1)任意の複素数$a,b$に対して$\overline{a\pm b}=\overline{a}\pm\overline{b},\overline{ab}=\overline{a}\overline{b}$が成り立つ.
(2)任意の複素数$z$に対して$Re(z)=\displaystyle \frac{1}{2}(z+\overline{z}),Im(z)=\frac{1}{2i}(z-\overline{z}),|z|= \sqrt{z\overline{z}}$,$z$が実数$,\Longleftrightarrow z=\overline{z},z$が純虚数$ \Longleftrightarrow z+\overline{z}=0$
$4\sqrt{3}+4i$の平方根をすべて求めよ.
level2
平面上に2点$A,B$がある.次の図形の方程式を$a,b$で表せ.
(1)直線$AB$
(2)線分$AB$の垂直二等分線
(3)線分$AB$を直径とする円
次の4つの数のうち複素数$a,b (|a|,|b|=1)$の値にかかわらず実数となるものをすべて選べ.
$\displaystyle\frac{ab+a+b+1}{a^2+b^2-1},\frac{ab(a+b)}{a^2b^2+a^2b+ab^2+a+b+1},\frac{a^3+b^3}{(a^2+b)(b^2+a)},\frac{(Re(a)+Im(b)i)(Re(b)+Im(a)i)}{Re(ab)+Im(ab)Re(\displaystyle\frac{a^2+b^2}{2ab})i}$
原点$O$,および原点でない異なる点$A,B$に対して三角形$OAB$の重心,外心の座標を求めよ.
level3
平面上に点$O$と点$A$に対して次のような操作を考える.
操作:点$A$を半直線$OA$上の$OA\cdot OA^{\prime}=1$を満たす点$A^{\prime}$に移す.
この操作を図形$X$上のすべての点に対して行ったとき$X$が移る先を$X^{\prime}$とおく.次のことを複素座標を用いて示せ.
(1)$X$が$O$を通らない円のとき,$X^{\prime}$も$O$を通らない円である.
(2)$X$が$O$を通る円のとき,$X^{\prime}$は$O$を通らない直線である.
複素座標を用いてスチュワートの定理を示せ.スチュワートの定理の主張は次のとおりである.
:三角形$ABC$の辺$BC$に点$P$を取ったとき,$AB^2\cdot CP+AC^2\cdot BP=BC(BP\cdot CP+AP^2)$が成り立つ.
次回予告
さて,複素座標入門第1回,どうだったでしょうか.問題を解くにはまだまだ使えそうにありませんね.次回は複素数の偏角の応用について書きます.
それでは,お疲れさまでした.
