ドラゴン曲線による平面充填定理の証明
以前の記事で書いたように、ドラゴン曲線を4つの方向に伸ばすと、それにより平面を覆うことができる。具体的には、平面を座標軸に平行な直線で区切って格子を作るときに、隣接格子点を結ぶ線分をどれもちょうど1回だけ通るように、4つの曲線を伸ばしていくことができる。こんな風に。
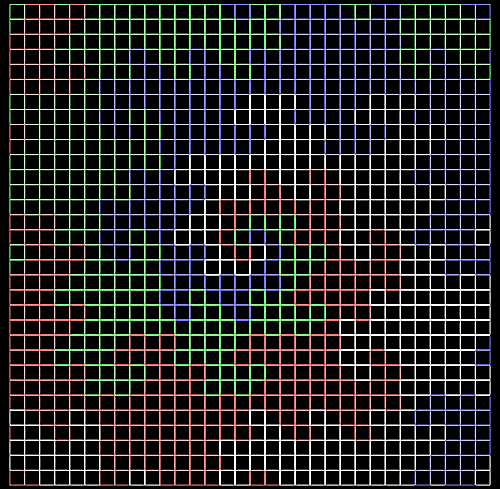ドラゴン充填1
このことを証明したい。それには、この形式だと具合が悪いので、$45$°回転させてこの形で証明する。
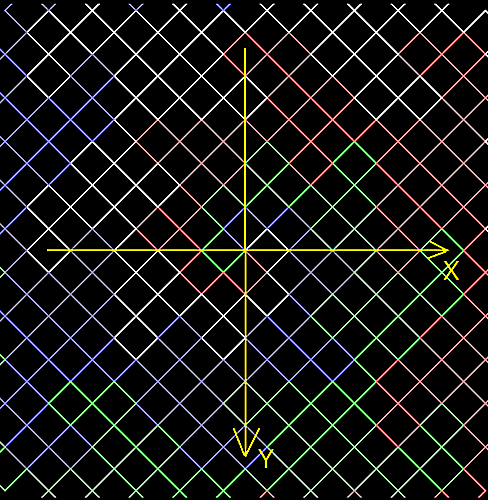ドラゴン充填2
座標軸はこのように取り、原点から4つの方向に伸ばすとする。長さについては軸との交わりが偶数の整数点$(\pm 2kとか\pm 2li)$、つまり各セグメントは$\sqrt{2}$の長さとする。複素数が活躍する。方針としては、ドラゴン曲線の構成法を見直すことにより、各セグメントの中点の全体を表す式を立てる。それらの全体と、次のような点：
$$\frac{m+ni}{2},~~~m,~nは共に奇数$$
という点の全体が1対1に対応することを示せば証明が終わる。すなわち、このような点は必ずいずれかのドラゴン曲線のいずれかのセグメントの中点であり、その表し方は一通りしかないことを言えばよい。
ドラゴン曲線復習
ドラゴン曲線は方向列$[0]$からスタートして
$$[0]\to[0,2]\to[0,2,4,2]\to[0,2,4,2,4,6,4,2]\to \cdots$$
のように変化していくもの。数字はモジュロ$8$の足し算で$\pi/4$に掛けて進行方向が出る。メソッドは、
$$[a_0,a_1,\cdots,a_{n-1}, a_{n-1}+2,\cdots ,a_1+2,a_0+2]$$
である。すなわち逆にたどって$2$を足す。上の図では、それを$8$分割で言うと$1,3,5,7$からスタートさせている。実際は$0$から始まるものだけ計算して角度をずらしているけど。
作品ページ
ソースコード：
let a = 0;
let b = 0;
let f = 0;
const SEG_SIZE = 40;
let palette = [[255, 255, 255], [120, 120, 255], [120, 255, 120], [255, 120, 120]];
function setup(){
createCanvas(640, 640);
background(0);
strokeWeight(2);
}
function draw(){
translate(320, 320);
let e = f & 1;
let h = 1;
while(f >= h){
if(!(f & h) && (f & (h * 2))){ e += 2; }
h *= 2;
}
c = SEG_SIZE * cos(e * PI / 2 - PI / 4);
s = SEG_SIZE * sin(e * PI / 2 - PI / 4);
let r = 4;
while(r--){
rotate(PI / 2);
stroke(...palette[r]);
line(a, b, a + c, b + s);
}
a += c;
b += s;
f++;
}
逆にたどって$2$を足すということは、$2$べきで区切った先の点はそこからスタートに戻る経路をたどるそれを、$-90$°回転させながら進むということ。こんな風に：
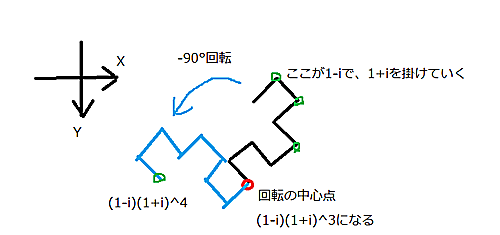説明
これらの$2$べき番目の点が重要である。白であらわされるドラゴン曲線の$2$べき項数の点（$0,1,2,4,8,\cdots$）は、まず$1$が$1-i$で、あとはそれに$1+i$を掛けて行ってできる点になる。すなわち、
$$0,~~1-i,~~(1-i)(1+i)^k~~~(k=1,2,3,4,\cdots)$$
この点を中心にそれまでの部分を$-90$°回転させて複製する行為を繰り返すわけ。それによりそれまでの曲線に乗っていた点$z$は、その時点での区切り点を$\alpha$として、
$$(-i)(z-\alpha) + \alpha = (-i)z + (1+i)\alpha$$
に移る。特に$z=0$は、
$$(-i)(0-\alpha)+\alpha = (1+i)\alpha$$
になる。だから区切り点は$1-i$から始まって$1+i$を繰り返し掛けていく感じになる。これが基本。
この白いドラゴン曲線のセグメントの中点の座標をこれから調べる。最初は$(1-i)/2$でそこからさっきの計算で求めていく。他の$3$つについては、これらを$90$°回転させて得られる。すなわち$-i$を$1,2,3$回掛けたものになる。
セグメントの中点を表す式
回転の中心を$\alpha$として、メソッド：
$$z~\to~(-i)z+(1+i)\alpha$$
を繰り返し適用する。
最初は$(1-i)/2$からスタートする。$\beta=(1-i)/2$とおく。最初の基準点である$1-i$を$\alpha=1-i$とおく。
$$\beta,~~(-i)\beta + (1+i)\alpha.$$
次の基準点は$(1+i)\alpha$でこれにより回転すると次が得られる：
$$(-i)\beta + (1+i)^2\alpha,~~(-i)^2\beta + (-i)(1+i)\alpha + (1+i)^2\alpha.$$
次の基準点は$(1+i)^2\alpha$でこれにより回転すると次が得られる：
- $(-i)\beta + (1+i)^3\alpha,$
- $(-i)^2\beta + (-i)(1+i)\alpha + (1+i)^3\alpha,$
- $(-i)^2\beta + (-i)(1+i)^2\alpha + (1+i)^3\alpha,$
- $(-i)^3\beta + (-i)^2(1+i)\alpha + (-i)(1+i)^2\alpha + (1+i)^3\alpha.$
次は$(1+i)^3\alpha$を基準として回転、これを繰り返す。すると、次のような形式の点が得られることになる。
$$(-i)^m\beta + (-i)^{m-1}(1+i)^{b_1}\alpha + \cdots + (1+i)^{b_m}\alpha.$$
ただし$m\geq 0$で$1\leq b_1<\cdots < b_m.~m=0$の点が$\beta$に対応する感じ。
これらはすべて$(-i)^0=1$で終わっている。それに$-i$を$1,2,3$回掛けることで、中点の座標がすべて得られる。すなわち、セグメントの中点の座標はすべて次の形式で表現される。
$$(-i)^{m+k}\beta + (-i)^{m+k-1}(1+i)^{b_1}\alpha + \cdots + (-i)^k(1+i)^{b_m}\alpha.$$
ただし$m\geq 0,~k=0,1,2,3,~1\leq b_1<\cdots < b_m.$
原点から$4$方向に延びるドラゴン曲線のセグメントの中点の座標の全体は次の式であらわされる。
$$\beta = (1-i)/2,~~~\alpha = 1-i,$$
$$(-i)^{m+k}\beta + (-i)^{m+k-1}(1+i)^{b_1}\alpha + \cdots + (-i)^k(1+i)^{b_m}\alpha.$$
ここに$m\geq 0$で（$m=0$の場合は$\beta$の$-i$倍の項だけ）、
$$1\leq b_1 < \cdots < b_m$$
であり、$k=0,1,2,3$である。$k$の値により、それに応じたドラゴン曲線の上の点であることが分かる。最高位の$b_m$で何回目の複製で得られる点であるかがわかる。
示すことは、すべての奇数点：
$$z = \frac{(2a+1) + (2b+1)i}{2}~~~~(a,b\mbox{は整数})$$
がこの形式で書けて、その書き方が一意であることである。
このままだと証明しづらいのでちょっといじる。$(-i)$の$1$ずつの降べきなので、$i$の$1$ずつの昇べきで書き直せる。また、どんな$i$のべきも$(-i)$の$0,1,2,3$のべきで書き直せる。だから次のような数の全体としてもいい。
$$\epsilon(\beta + i(1+i)^{b_1}\alpha + i^2(1+i)^{b_2}\alpha + \cdots + i^m(1+i)^{b_m}\alpha), $$
$$\epsilon \in \{1,~i,~-1,~-i\},~~~~m\geq 0,~~~~1\leq b_1 < \cdots < b_m.$$
$\epsilon$も$i$のべき、というかガウス整数環の単元。この形式で証明する。
表現の一意性の証明
一意性の証明。帰納法による。
\begin{align*}
&\epsilon(\beta + i(1+i)^{b_1}\alpha + \cdots + i(1+i)^{b_m}\alpha) \\[5pt]
&=\epsilon'(\beta + i(1+i)^{b_1'}\alpha + \cdots + i(1+i)^{b_{m'}'}\alpha)
\end{align*}
だとする。まず両辺に$1+i$を掛ける。すると、
$$(1+i)\beta = 1,~~~(1+i)\alpha=2$$
だから、
\begin{align*}
&\epsilon(1 + 2i(1+i)^{b_1} + \cdots + 2i(1+i)^{b_m}) \\[5pt]
&=\epsilon'(1 + 2i(1+i)^{b_1'} + \cdots + 2i(1+i)^{b_{m'}'})
\end{align*}
となる。$b_1$も$b_1'$も$1$以上だからこれは
$$\epsilon(1 + (2+2i)\zeta) = \epsilon'(1+(2+2i)\zeta')~~~(\zeta,~\zeta'\in \mathbb{Z}[i])$$
と書ける。これよりモジュロ$2+2i$で$\epsilon\epsilon'^{-1}\equiv 1$となるが、$2,~1-i,~1+i$はいずれも$2+2i$で割り切れないから、$\epsilon\epsilon'^{-1}=1$で$\epsilon=\epsilon'$を得る。すなわち二通りに書けるとき単元部分は等しい。ゆえに、
$$(1+i)^{b_1} + \cdots + (1+i)^{b_m} = (1+i)^{b_1'} + \cdots + (1+i)^{b_{m'}'}$$
となる。このことからどっちかの$m$が正ならもう片方の$m'$も正になることが分かる。
次に、たとえば$b_1< b_1'$とすると、両辺を$(1+i)^{b_1}$で割って、
$$1 + (1+i)^{b_2-b_1} + \cdots + (1+i)^{b_m-b_1} = (1+i)^{b_1'-b_1} + \cdots + (1+i)^{b_{m'}'-b_1}$$
となるが、$1+i$の指数はすべて正だから、実部と虚部のパリティを考えると矛盾である。よって$b_1=b_1'$で、両辺からこれを除く。
これを繰り返す。すると、$m\neq m'$だとどっちかが先に$0$になってしまうから矛盾と分かる。だから$m=m'$で、さらに指数はすべて一致する。これで示された。$\square$
表現可能性の証明
次を示す。
複素数$z$は次の形とする。
$$z = \frac{(2a+1)+(2b+1)i}{2},~~~~a,bは整数。$$
このとき、$z$を次のように書ける。
$$z = \epsilon(\beta + i(1+i)^{b_1}\alpha + \cdots + i^m(1+i)^{b_m}\alpha).$$
$$(\epsilon \in \{1,~i,~-1,~-i\},~~~\beta = \frac{1-i}{2},~~~\alpha = 1-i,~~~m\geq 0,~~~1\leq b_1<\cdots < b_m)$$
まず$p=2a+1,~q=2b+1$とおく。これらは奇数。
$$w = (1+i)z = \frac{p-q}{2} + \frac{p+q}{2}i = s+ti$$
とおくと、$s-t,s+t$は奇数だから、$s,t$はパリティが異なる。そこで、これとモジュロ$2+2i$で等しい単元を取る。これは一意的に存在する。まずモジュロ$2+2i$の代表元は$8$つで、
$$0,~1+i,~1-i,~2,~1,~i,~-1,~-i$$
が取れる。このうち実部と虚部のパリティが異なるものが同値となるのはもちろん後者$4$つ、つまり単元。単元同士はモジュロ$2+2i$で等しいと一致する。よって、
$$w = \epsilon + (2+2i)\zeta,~~~\zeta\in\mathbb{Z}[i]$$
と書けて、
$$z= \epsilon\beta + 2\zeta = \epsilon\beta + i\epsilon(1+i)\zeta'\alpha~~~~(\beta = \frac{1-i}{2},~~\alpha=1-i,~~\zeta'=(-i)\epsilon^{-1}\zeta)$$
と書ける。これより、
$$z = \epsilon(\beta + i(1+i)\zeta'\alpha)$$
だから、あとは$\zeta'$というか一般のガウス整数$\zeta$が次のように書けることを言えばよい：
$$\zeta = (1+i)^{c_1} + i(1+i)^{c_2} + \cdots + i^{m-1}(1+i)^{c_m}.$$
$$m\geq 1,~~0\leq c_1 < c_2 < \cdots < c_m. $$
なお、$\zeta=0$の場合、つまり$z$が$\beta$の単元倍の場合はすでに終わっているので、以下ではそうでないとする。$\square$
任意の$0$でないガウス整数$\zeta\in\mathbb{Z}[i]$は次の形式に書ける：
$$\zeta = (1+i)^{c_1} + i(1+i)^{c_2} + \cdots + i^{m-1}(1+i)^{c_m}.$$
ただし$m\geq 1,~~0\leq c_1< c_2<\cdots < c_m.$
$N=|\zeta|^2$は整数なので、これにもとづいて無限降下法で示す。
- $N=1,$すなわち$\zeta$が単元の場合
次のように示される：
$$1=1,~~~i=1 + i(1+i),~~~-1 = 1 + i(1+i)^2,$$
$$-i = 1 + i(1+i) + i^2(1+i)^2.$$
- $N \leq 6$の場合。
$|\zeta|^2 = N \leq 6$であるようなガウス整数を考える。
$$x^2+y^2=3,~~~x^2+y^2=6$$
を満たす整数組$(x,y)$は存在しない。$N=1$は単元の場合である。$N=2$は$1+i$の単元倍の時で、$N=4$は$2i$の単元倍の時であるが、$2i=(1+i)^2$でありいずれも先程の単元をあらわす式で両辺に$1+i$や$(1+i)^2$を掛ければ表示が得られる。
最後に$N=5,$これは$8$つある。$2+i$の単元倍と$2-i$の単元倍である。
注意：ガウス整数$\zeta$が目的の表示で書けるならば、
$$\zeta' = 1+i(1+i)^b\zeta~~~~(b\geq 1)$$
もまた目的の表示で書ける。証明は容易。
\begin{align*}
2+i&=1+(1+i)=1+i(1+i)\cdot (-i)\\[5pt]
2-i &= 1+(1-i) = 1+i(1+i)\cdot (-1)\\[5pt]
1+2i&=1+i(1+i)\cdot (1-i)\\[5pt]
1-2i&=1+i(1+i)\cdot(-1+i)
\end{align*}
とでき、いずれもドットの後ろを表記で書き換えればよい。次に、
\begin{align*}
-2+i &= 1+(-3+i) = 1+i(1+i)\cdot(2+i)\\[5pt]
-2-i&=1+i(1+i)\cdot (1+2i) \\[5pt]
-1+2i &= 1+i(1+i)\cdot 2\\[5pt]
-1-2i &= 1+i(1+i)\cdot 2i
\end{align*}
とできるから成り立つ。
- $|\zeta|^2 = N > 6$とし、$|\zeta'|^2< N$なる$\zeta'$については成立しているとき
はじめに$\zeta$の実部と虚部のパリティが等しい時。この場合$\zeta$は$1+i$で割れる、つまり割ったものもガウス整数。だから$\zeta=(1+i)\zeta'$と書けるがこのとき
$$|\zeta'|^2=\frac{|\zeta|^2}{2}<|\zeta|^2$$
なので$\zeta'$に仮定が使える。それに$1+i$を掛ければ得られる。
次にパリティが異なるとき。この場合$\zeta-1$を考えるとこれはパリティが一致するから$1+i$で割れる。特に$i(1+i)$で割れるので
$$\zeta = 1 + i(1+i)\zeta'$$
のように書ける。ここで、
$N\geq 6 > (1+\sqrt{2})^2,~~~|\zeta| = \sqrt{N} > 1+\sqrt{2}$
だから、
$$|\zeta'| = \frac{|\zeta-1|}{\sqrt{2}}\leq \frac{1}{\sqrt{2}}(|\zeta| + 1)$$
において
$$1<\frac{|\zeta|}{1+\sqrt{2}}$$
を適用して
$$|\zeta'|\leq \frac{1}{\sqrt{2}}(|\zeta|+1)<\frac{1}{\sqrt{2}}(1+\frac{1}{1+\sqrt{2}})|\zeta|=|\zeta|.$$
$$\therefore~~~|\zeta'|^2<|\zeta|^2.$$
ここで$\zeta'$は仮定を満たすから表記で書ける。ゆえに$\zeta$も表記で書ける。証明終わり。$\square$
テルドラゴンの方
多分うまくいったのはガウス整数環$\mathbb{Z}[i]$が綺麗な性質を持ってたからだと思う。テルドラゴンの敷き詰めの方では$\mathbb{Z}[\omega]$が活躍しそうな気がするけど証明はまだできてないのでそのうちやってみたい。
