【高校数学ⅠAⅡB】y=f(x)のグラフを平行移動・拡大縮小・回転移動させたい
初めに
関数$f(x)$を変形させてみたいと思ったことはあるだろうか?僕はあります。
方針
平行移動、拡大縮小、回転移動をやって行くのだが、この3つとも次に示す方針に従って行っていく。
$$1.\ 点(x,y)が変換されて点(X,Y)となったとする。 \\\hspace{ 10pt }そのとき、X=(変換の定義の式)、Y=(変換の定義の式)と置く。$$
$$2.\ この2式をx,yについて解く$$
$$3.\ y=f(x)に2.で示したx,yを代入する。$$
平行移動
$$y=f(x)のグラフをx軸方向にp、y軸方向にqだけ平行移動させたグラフの式を求めよ。$$
$$xがx軸方向にpだけ移動されXとなり、yがy軸方向にqだけ移動されYとなるから、$$
$$X=x+p、Y=y+qとなる。$$
$$これをx,yについて解くと、$$
$$x=X-p、y=Y-q$$
$$したがって、$$
$$Y-q=f(X-p)が得られる。$$
$$よって、この公式が得られる。$$
$$y=f(x)のグラフをx軸方向にp、y軸方向にqだけ平行移動させたグラフの式は、$$
$$y-q=f(x-p)$$
GeoGebraで出力してみる
 平行移動
平行移動
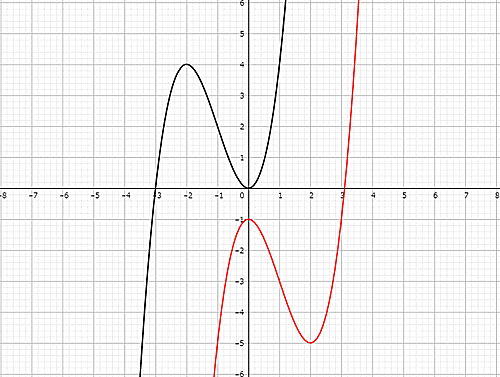
黒いグラフは$y=x^3+3x^2$、赤いグラフはそれを$x方向に2,y方向に-5$だけ平行させたグラフである。
つまり、$y+5=(x-2)^3+3(x-2)^2 \Longleftrightarrow y=x^3-3x^2-9$である。
拡大縮小
$$y=f(x)のグラフを原点を中心にx軸方向にp倍、y軸方向にq倍拡大させたグラフの式を求めよ。$$
ちなみに、縮小したい場合も本質的には同じである。$(0< p,q<1か1< p,qかの違い)$
$$xがx軸方向にp倍されてXとなり、yがy軸方向にq倍されてYとなるから、$$
$$X=px、Y=qyとなる。$$
$$これをx,yについて解くと、$$
$$x=\frac Xp、y=\frac Yqとなる。$$
$$したがって、$$
$$\frac Yq=f(\frac Xp)が得られる。$$
$$よって、この公式が得られる。$$
$$y=f(x)を原点中心にx軸方向にp倍、y軸方向にq倍拡大させたグラフの式は、$$
$$\frac yq=f(\frac xp)$$
$$なお、p=-1にすればy軸で対称移動、q=-1にすればx軸で対称移動させることができる。$$
GeoGebraで出力してみる
 拡大縮小
拡大縮小
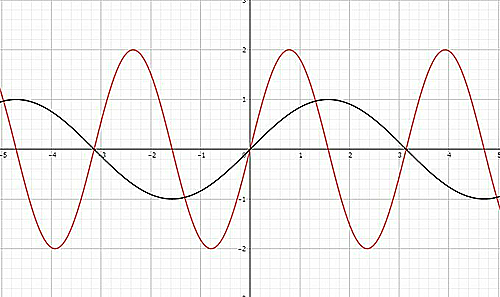
黒いグラフは$y=\sin x$、赤いグラフはそれを原点中心に$x方向に\frac 12倍に縮小し,y方向に2倍拡大させた$グラフである。
$$つまり、\frac y2=\sin 2x \Longleftrightarrow y=2\sin 2xである。$$
回転移動
$$y=f(x)のグラフを原点中心にθだけ回転移動させたグラフの式を求めよ。ただし、0 \leqqθ<2\piとする。$$
$$(x,y)=(r\cos\alpha,r\sin\alpha)とする。(極形式に直す.)$$
$$すると、(X,Y)=(r\cos(\alpha+θ),r\sin(\alpha+θ))となる。$$
$$したがって、$$
$$X=r\cos(\alpha+θ)
\\\hspace{ 8pt }=r(\cos\alpha\cosθ-\sin\alpha\sinθ)
\\\hspace{ 8pt }=(r\cos\alpha)\cosθ-(r\sin\alpha)\sinθ
\\\hspace{ 8pt }=x\cosθ-y\sinθ$$
$$Y=r\sin(\alpha+θ)
\\\hspace{ 8pt }=r(\sin\alpha\cosθ+\cos\alpha\sinθ)
\\\hspace{ 8pt }=(r\cos\alpha)\sinθ+(r\sin\alpha)\cosθ
\\\hspace{ 8pt }=x\sinθ+y\cosθ
$$
$$よって、$$
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
X=x\cosθ-y\sinθ \\
Y=x\sinθ+y\cosθ
\end{array}
\right.
\end{eqnarray}
$$
$$この方程式をx,yについて解くと、$$
$$x=X\cosθ+Y\sinθ、y=-X\sinθ+Y\cosθ$$
この連立方程式を解く際に$\sinθ,\cosθ$で割る場面が出たため、$θ=0,\frac{\pi}{2},\pi,\frac 32\pi$とそれ以外で場合分けをし、この解が成立することを示す必要がある。なお、確認すれば上の式はこれらの場合でも成り立つ。
よって、
$$-X\sinθ+Y\cosθ=f(X\cosθ+Y\sinθ)が得られる。$$
$$よって、この公式が得られる。$$
$$y=f(x)を原点中心にθだけ回転移動させたグラフの式は、$$
$$-x\sinθ+y\cosθ=f(x\cosθ+y\sinθ)$$
GeoGebraで出力してみる
 回転移動
回転移動
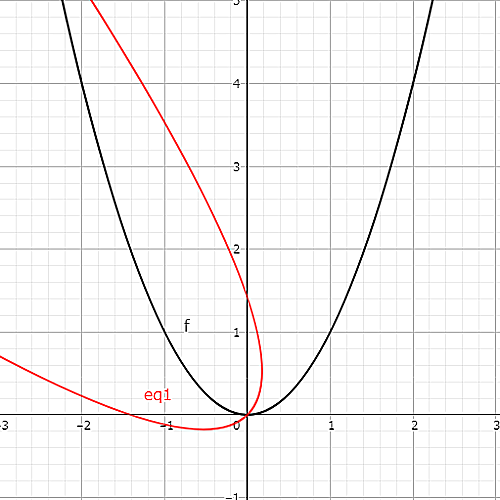
黒いグラフは$y=x^2$、赤いグラフはそれを原点中心に$\frac\pi4$($45°$)だけ回転移動させたグラフである。
$$-x\sin\frac\pi4+y\cos\frac\pi4=(x\cos\frac\pi4+y\sin\frac\pi4)^2 \Longleftrightarrow
\frac12x^2+xy+\frac12y^2+\frac{1}{\sqrt{2}}x-\frac{1}{\sqrt{2}}y=0$$
となる。
考察
$x,y$を上手いこと置換して計算しているだけなので、今まで考えてきた陽関数だけでなく、陰関数でも定義できそう。
また、回転移動の導出方法は、今回やった加法定理による導出以外にも、複素平面を利用したり行列を利用したりと、色々な解法があって面白かった。
