複素座標入門2/5 偏角の応用
どうもnatuです.今回は偏角についてです.複素座標をする上でこの偏角の考え方が一番大事です.この回で述べる命題は後の回でも頻繁に使うので是非マスターしましょう.では,参ります.
絶対値と偏角
複素数は実部と虚部を決めるとただ一つに定まります.実はこのような複素数を決定する要素としてほかに絶対値と偏角があります.
絶対値
絶対値は第1回でも登場しましたが,もう少し踏み込みます.
$z$の絶対値とは複素数平面上において$z$と対応する点と原点,すなわち$0$と対応する点との距離を言い,$|z|$で表します.
三平方の定理より$|z|= \sqrt{Re(z)^2+Im(z)^2}$ですね.
絶対値について次の重要なことが成り立ちます.
$|ab|=|a||b| \left|\displaystyle\frac{1}{z}\right|= \displaystyle\frac{1}{|z|} (|z| \neq0)$
第1式 左辺$=|(Re(a)+Im(a)i)(Re(b)+Im(b)i)|$
$=|(Re(a)Re(b)-Im(a)Im(b))+(Re(a)Im(b)+Im(a)Re(b))i|$
$=\sqrt{(Re(a)Re(b)-Im(a)Im(b))^2+(Re(a)Im(b)+Im(a)Re(b))^2}$
$=\sqrt{Re(a)^2Re(b)^2+Re(a)^2Im(b)^2+Im(a)^2Re(b)^2+Im(a)^2Im(b)^2}$
$=\sqrt{Re(a)^2+Im(a)^2}\sqrt{Re(b)^2+Im(b)^2}=$右辺
よって示された.
第2式 第1式において$a=z,b= \displaystyle\frac{1}{z}$として得られる.
積の絶対値=絶対値の積 ってことですね.大事です.
偏角
$z$の絶対値とは,複素平面上において$z$と対応する点$Z$と原点$O$と$A(1)$について半直線$OZ$が半直線$OA$となす角をいい,$\arg z$と表します.
「なす角」は符号付き角を考えます.すなわち$\angle AOZ=-\angle ZOA$ということです.
「実部・虚部」に注目せず「絶対値・偏角」で複素数$z$を表したいときは次の表し方が有効です.
$z=r(\cos\theta+i\sin\theta)$ この表し方は極座標に似た表し方であるので"極形式"と呼ばれます.
当たり前ですが偏角が1周$(2\pi)$してもその複素数は不変なので,複素数の偏角というとその角度を限定するために大抵は$0\leq\theta<2\pi$または$-\pi\leq\theta<\pi$で考えます.
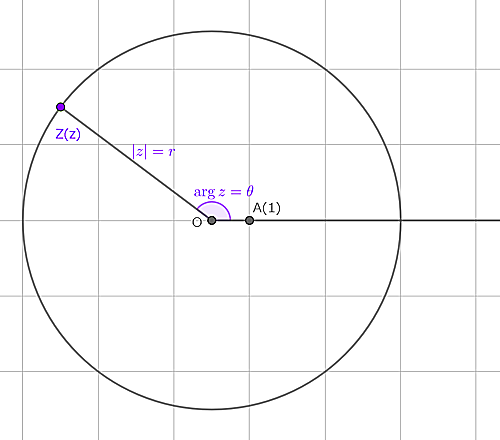 図
図
$\arg ab=\arg a+\arg b \arg \displaystyle\frac{1}{z}=-\arg z (z\ne 0)$
第1式 練習問題とする.
第2式 第1式において$a=z,b= \displaystyle\frac{1}{z}$として得られる.
積の偏角=偏角の和 ってことですね.超大事です.
直線のなす角
直線の平行・垂直1
平面上に2点$A,B$があるとき半直線$AB$が実軸となす角はどう表せるでしょうか.
考えられるのはこの直線を平行移動して$O$と$A$を重ねたとき,$B$の行先は$b-a$に対応するので求める角は$\arg (b-a)$で表せるという考え方です.もう少し拡張しましょう.
新しく2点$C,D$をとって,半直線$AB$が半直線$CD$となす角を表します.
求める角は半直線$AB$が実軸となす角から半直線$CD$が実軸となす角を引いたものに等しいですね.ということで$\arg (b-a)-\arg (d-c)=\arg \displaystyle\frac{b-a}{d-c}$です.
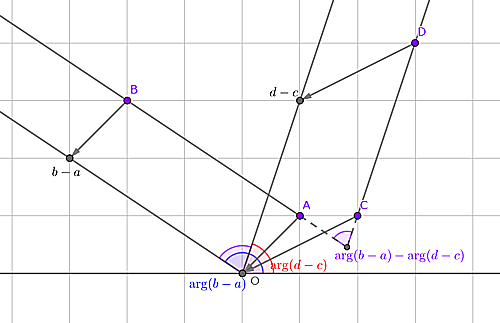 図
図
特に,$d$を$c$に,$c$を$a$に置き換えると半直線$AB$が半直線$AC$となす角,すなわち$\angle BAC$を複素数の偏角として表すことができます.
$\angle BAC=\arg\displaystyle\frac{a-b}{a-c}$
この命題は超超超重要です.
さらに我々が興味を持つのは,直線$AB,CD$が平行or垂直になるときです.
平行なとき
半直線$AB$が半直線$CD$となす角は$0$または$\pi$なので$\arg\displaystyle\frac{b-a}{d-c}=0,\pi$です.
このとき複素数$\displaystyle\frac{b-a}{d-c}$は実軸上に存在するので実数といえます.
垂直なとき
半直線$AB$が半直線$CD$となす角は$ \displaystyle\frac{1}{2}\pi$または$ \displaystyle\frac{3}{2}\pi$なので$\arg\displaystyle\frac{b-a}{d-c}= \displaystyle\frac{1}{2}\pi, \displaystyle\frac{3}{2}\pi$です.
このとき複素数$\displaystyle\frac{b-a}{d-c}$は虚軸上に存在するので純虚数といえます.
まとめます.
$AB/\!/ CD \Longleftrightarrow \displaystyle\frac{b-a}{d-c}$は実数 $AB\perp CD \Longleftrightarrow \displaystyle\frac{b-a}{d-c}$は純虚数
点$A$と点$D$が一致する,すなわち$a=d$のときこの命題は次のようになります.
3点$A,B,C$が同一直線上に存在$ \Longleftrightarrow \displaystyle\frac{a-b}{a-c}$は実数
$\angle BAC=90^{\circ} \Longleftrightarrow \displaystyle\frac{a-b}{a-c}$は純虚数
これは証明問題に使えますね.
直線の平行・垂直2
今度は直線の関係を方程式から考察します.
今,直線の方程式$az+b\overline{z}=c \cdots $①があります.
平行な直線
直線①を$p$だけ平行移動した直線は$z$を$z-p$にした式,すなわち$a(z-p)+b(\overline{z-p})=c$として得られますね.これを整理して$ap+b\overline{p}+c=d$とすると,$az+b\overline{z}=d$となります.式①と比べてみてください.$c$が$d$になっただけですね!
垂直な直線
直線①を原点を中心に$90^{\circ}$だけ回転移動した直線は$z$を$\displaystyle\frac{z}{i}$にした式,すなわち$a\displaystyle\frac{z}{i}+b\overline{(\displaystyle\frac{z}{i})}=c$として得られますね.これを整理して$az-b\overline{z}=ci$さらに$ci$をほかの複素数,例えば$d$にしても平行移動するだけなので$az-b\overline{z}=d$は①と垂直ですね!
直線①上の点$Z(z)$を原点を中心に$90^{\circ}$だけ回転移動すると点$Z^{\prime}(z^{\prime})$に移り,$z^{\prime}=iz$がなり立ちます.なのでこれを$z=\displaystyle\frac{z^{\prime}}{i}$と変形して①に代入,$z^{\prime}$を$z$と置きなおせばよいのです.図形の平行移動と似た考えですね.
まとめます.
任意の複素数$a,b,c,d$について,
2直線$az+b\overline{z}=c,az+b\overline{z}=d$は平行
2直線$az+b\overline{z}=c,az-b\overline{z}=d$は垂直
それでは練習問題を解いてみましょう.
練習問題
level1
直交座標平面上に異なる3点$A(m,n),B(-n,m),C(m-n,m+n)$がある.
複素座標を用いて$\angle BAC=45^{\circ}$を示せ
直線$az+b\overline{z}=c (a \neq0)$と原点の距離は$b$によらないことを示せ.
(1)絶対値が$r$で偏角が$\theta$である複素数$\alpha$について$Re(\alpha),Im(\alpha)$を求めよ.
(2)(1)の結果を用いて$|ab|=|a||b|,\arg ab=\arg a+\arg b$が成り立つことを示せ.
level2
三角形$ABC$が正三角形であるとき,$a^3+b^3+c^3=3abc$であることを示せ.
${}_{99} \mathrm{ C }_0+{}_{99} \mathrm{ C }_4+\cdots +{}_{99} \mathrm{ C }_{96}$を計算せよ.
4点$\displaystyle A(a),B(b),A^{\prime}\left(-\frac{1}{\overline{a}}\right),B^{\prime}\left(-\frac{1}{\overline{b}}\right)$は同一直線上に並ぶか同一円周上に並ぶことを示せ
level3
平面上に三角形$ABC$があり,外部に点$P,Q,R,S$を四角形$ABPQ,ACRS$が正方形になるようにとる.点$A$を通り,直線$QS$に垂直な直線は辺$BC$の中点を通ることを示せ.(長岡の教科書Ⅲより)
平行四辺形$ABCD$があり,直線$AB$上に点$E$がある.$A,B,E$はこの順に並んでおり,$BC=BE$をみたす.$A$から直線$CE$へおろした垂線と線分$AE$の垂直二等分線の交点を$X$とするとき,4点$A,B,D,X$は同一円周上にあることを示せ.$(EGMO$一次予選$2020 4)$
次回予告
だんだんとただの数だった複素数が図形的に扱えるようになってきましたね.実用的でしょう?
さて,次回からは外接円が$|z|=1$の三角形について書いていこうと思います.これが理解できればたいていの問題は(複素で解くことを想定しているならば)手が届きます!
それでは,お疲れさまでした.
