自作問題1(解答編)

自作問題1の解答です。
https://mathlog.info/articles/106

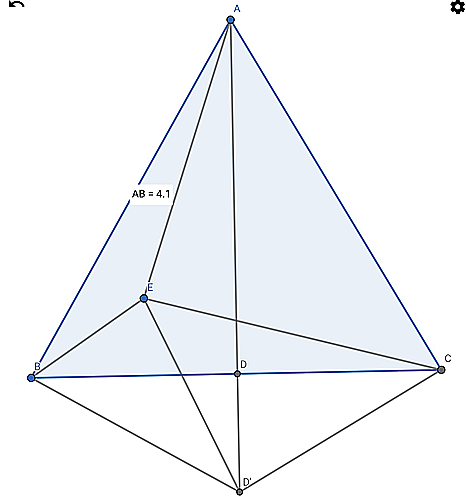図
(上の図において、点P→点Eとなっています。ABの長さの表示は気にしないで…)
<解答>
BCの中点をD，三角形BPCの外心をOとする。
(図では点O→点D’となっています。)
このとき、角BOC＝120°，BO＝PO＝CO＝2√3，
AO＝4√3である。
三角形APOで余弦定理より、
$\cos \angle AOP$＝$\frac{11}{12}$
$BP\lt CP$より，
$\cos \angle POB= \cos (60°- \angle AOP) = \frac{11+ \sqrt{69}}{24} $
三角形BPOで余弦定理より，
$BP^2 = 13- \sqrt{69} $
したがって，
$ BP＝\frac{ \sqrt{46}- \sqrt{6}} {2} $$ \cdots $(答)

別解等思いつきましたら教えていただけると嬉しいです。

追記

<考え方>
図形における求値問題は、大雑把に分けて以下の２つ。
1、条件を満たす図形が一意(あるいは有限個のパターンに)
決定される。
2、条件を満たす図形は一意に決まらないが、求める値は
常に一定。
今回は前者です。
(前者より後者の方が難問が多い印象)
①角BPCの大きさが一定→点Pはある円上にある！
②APの長さが一定→点Pは①とは別の円上にある！
③だから点Pは二つの円の交点だ！
④BPとCPの大小関係から点Pが一意に決まる！
と考えました。こう考えると三角形BPCの外心を
補助点としてとる事は自然な考えだと言えそうです。
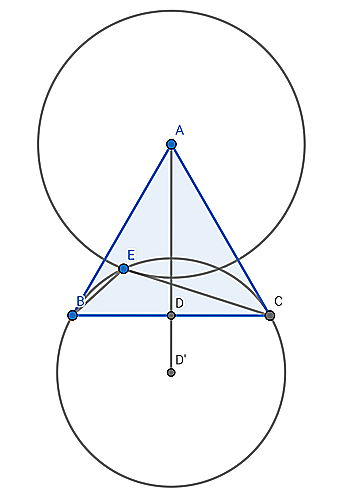図2