4元体について

「素数に憑かれた人たち」P316に四元体であるF4の演算表が載っています。ルールがよくわからないので頑張って調べました。

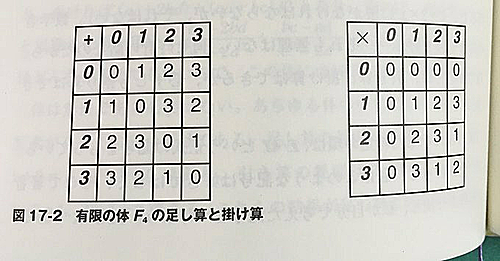4元体

もし間違っていたら指摘してください。

加算
F4の任意の元xとyについて、x+yを正の整数で計算した結果を「N:x+y=z」と書き、同様にF4上で計算した結果を「F4:x+y=z」と書きます。

ルール1
(x=y)→F4:x+y=0

ルール2
N:x+y=4→F4:x+y=2
N:x+y=5→F4:x+y=1

ただしルール1を優先する。

ルール3
N:x+y=1→F4:x+y=1
N:x+y=2→F4:x+y=2
N:x+y=3→F4:x+y=3

ただしルール1、ルール2を優先する。

積算
加算と同様にF4の任意の元xとyについて、x×yを正の整数で計算した結果を「N:x×y=z」と書き、同様にF4上で計算した結果を「F4:x×y=z」と書きます。

ルール1
x=2またはx=3、かつy=2またはy=3ならば
F4:x×y=N:|x×y-7|

ルール2
F4:x×y=N:x×y
ただしルール1を優先する。

実に複雑だ。もっと簡単に書けないものか。