

&&&def 三角数
三角数とは、以下のように石を用いて正三角形を構成した場合に用いる石の総数で表される数のことである。
　三角数のなす数列は1, 3, 6, 10, 15, 21, 28, 36, ... 
となり、$\normalsize{n}$項目は$\normalsize{k(k+1)/2}$である。
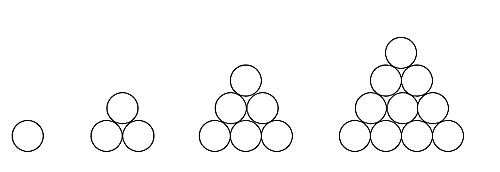![三角数](/uploads/mathdown/20201205144427.jpg =250)
&&&


&&&thm 
$N\equiv 3\pmod 8$を満たす自然数$\normalsize{N}$は奇数の平方数3つの和として表すことができる。（証明略）
&&&


&&&thm
任意の自然数は3つの三角数の和として表すことが出来る。
&&&


&&&prf
定理1より、3つの非負整数$\normalsize{a}$,$\normalsize{b}$,$\normalsize{c}$を用いて
$\normalsize{8N+3}$$=$$\normalsize{(2a+1)^{2}+(2b+1)^{2}+(2c+1)^{2}}$
と表される。これを変形して
$\normalsize{N}$$=$$\normalsize{a(a+1)/2+b(b+1)/2+c(c+1)/2}$
を得る。

&&&





Gaussの定理（三角数）

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント