集合論による関係データモデルの定式化
はじめに
この記事では集合論をベースに関係データモデルの話の定式化を試みています。ネットなどにある関係データモデルの解説ではあまり数式を用いずに解説しているものが多く、数学的に曖昧なことが多いです(大学の講義もそうでした)。そこで、集合論をベースに関係データモデルの話の定式化をしようと考えました。関係データモデルのようなデータベースの話については大学の講義で習った程度の初学者なので間違えている部分がありましたら申し訳ありません。
関係データモデルの定義から2NFの定義までを書いていきたいと思います。
前提(集合論)
この記事で必要になる集合論の話を軽く紹介します。
$X, Y$を集合とし、$A \subseteq X$とします。写像$f\colon X\to Y$に対して、写像$f|_A\colon A\to Y$を
$$f|_A(x) = f(x)\quad (x\in A)$$
で定義します。写像$f|_A\colon A\to Y$を写像$f$の集合$A$への制限と呼びます。
2つの写像$f,g\colon \set{0,1,2,3}\to \Z$を$f(n) = n, g(n)=n^2$で定義します。
$(f(0), f(1)) = (g(0), g(1))$なので、$f|_{\set{0,1}} = g|_{\set{0,1}}$が言えます。
$\Lambda$を集合とします。$(A_\lambda)_{\lambda\in \Lambda}$を添字集合$\Lambda$によって添字付けられた集合族とします(つまり、各$\lambda \in \Lambda$に対して$A_\lambda$を集合とします)。このとき、集合$\prod_{\lambda \in \Lambda} A_\lambda$を
$$
\prod_{\lambda \in \Lambda} A_\lambda = \setsep{f\colon \Lambda \to \bigcup_{\lambda\in\Lambda}A_\lambda}{f(\lambda) \in A_\lambda\ (\forall \lambda \in \Lambda)}
$$
で定義します。$\prod_{\lambda \in \Lambda} A_\lambda$を$(A_\lambda)_{\lambda\in \Lambda}$の直積と呼びます。
$\Lambda=\set{1,2}, A_1=\set{3,4,5}, A_2=\set{6,7}$とします。このとき、$\prod_{\lambda \in \Lambda} A_\lambda$には次の6個の元($f_1,...,f_6$)があります
| $\lambda=1$ | $\lambda=2$ | |
|---|---|---|
| $f_1(\lambda)$ | 3 | 6 |
| $f_2(\lambda)$ | 3 | 7 |
| $f_3(\lambda)$ | 4 | 6 |
| $f_4(\lambda)$ | 4 | 7 |
| $f_5(\lambda)$ | 5 | 6 |
| $f_6(\lambda)$ | 5 | 7 |
関係データモデルの定義
次に定義される$P, D, R$の3つ組$\langle P, D, R\rangle$ を関係データモデルと呼ぶことにします。
- $P$: 集合
- $D= (D(A))_{A\in P}$: 集合$P$によって添字付けられた集合族
- $R \subseteq \prod_{A\in P}D(A)$
$P$の元を属性(attribute)、$R$の元をタプル(tuple)と呼びます。また、$R$を関係(relation)と呼びます(集合論でも、直積の部分集合を関係と呼んだりしますね。)
$P_1 = \set{a,b,c}$、$D_1(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_1)$、$R_1=\setsep{t\in \prod_{A\in P_1}D_1(A)}{t(a) + t(b) + t(c) =3}$
とすると、$\langle P_1, D_1, R_1\rangle$は関係データモデルです。
このモデルを表に表すと次のようになります。
| $a$ | $b$ | $c$ |
|---|---|---|
| 0 | 0 | 3 |
| 0 | 1 | 2 |
| 0 | 2 | 1 |
| 0 | 3 | 0 |
| 1 | 0 | 2 |
| 1 | 1 | 1 |
| 1 | 2 | 0 |
| 2 | 0 | 1 |
| 2 | 1 | 0 |
| 3 | 0 | 0 |
(○3つと|2つの並べ方から10通りあります。)
$a,b,c$は属性です。表の横の並び($(0,0,3)$や$(0,1,2)$など)はタプルです。この記事の文脈に沿って正確に言うと、例えば$(t(a), t(b), t(c))=(0,0,3)$で定義される写像$t$がタプルです。
$P_2 = \set{a,b,c}$、$D_2(A) = \set{0,1}\ (A\in P_2)$、$R_2=\setsep{t\in \prod_{A\in P_2}D_2(A)}{t(c) = \max\set{t(a), t(b)}}$
とすると、$\langle P_2, D_2, R_2\rangle$は関係データモデルです。
このモデルを表に表すと次のようになります。
| $a$ | $b$ | $c$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(ORの真理値表です。)
関係データモデルを考えていると、「2つのタプル$t_1, t_2\in R_2$の属性$a$と属性$c$の値が等しい」ということを数式で書きたくなることがあります。もちろん$(t_1(a), t_1(c)) = (t_2(a), t_2(c))$と書けばいいのですが、写像の制限を用いて$t_1|_{\set{a,c}} = t_2|_{\set{a,c}}$と簡潔に書くことができます。
例えば、$t_1, t_2\in R_2$を$(t_1(a), t_1(b), t_1(c)) = (1,0,1), (t_2(a), t_2(b), t_2(c)) = (1,1,1)$で定義すると、$t_1 \neq t_2$ですが、$(t_1(a), t_1(c)) = (t_2(a), t_2(c))$なので、$t_1|_{\set{a,c}} = t_2|_{\set{a,c}}$が言えます。
ちなみに、$t_1$と$t_1|_{\set{a,c}}$を表で表すと次のようになります。
[$t_1$の表]
| $a$ | $b$ | $c$ |
|---|---|---|
| 1 | 0 | 1 |
[$t_1|_{\set{a,c}}$の表]
| $a$ | $c$ |
|---|---|
| 1 | 1 |
今後は写像の制限を用いた表記を使います。
関数従属性
$\langle P, D, R\rangle$を関係データモデルとします。
2つの属性の集合$X,Y\subseteq P$について、「任意の$t_1, t_2\in R$に対して、$t_1|_X = t_2|_X$ならば$t_1|_Y = t_2|_Y$」
が成り立つとき、$Y$は$X$に関数従属しているといい、$X\to Y$と書きます。
雑にいうと、$X$に属している属性の値がすべて決まれば、$Y$に属している属性の値がすべて決まるということです。
余談ですが、関数従属性の定義は 二項関係から写像を定義する際に使う「右一意」 や 単射の定義 とよく似てますね。
$P_1 = \set{a,b,c}$、$D_1(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_1)$、$R_1=\setsep{t\in \prod_{A\in P_1}D_1(A)}{t(a) + t(b) + t(c) =3}$
で定義される、関係データモデル$\langle P_1, D_1, R_1\rangle$における関数従属性を見ていきます。
$\set{a,b}\to \set{c}$が成り立ちます。
これは雑に言うと、属性$a$と属性$b$の値が決まれば属性$c$の値も決まるということです。
このことについて見ていきます。
$t\in R_1$とします。このとき、$t(c) = 3 - t(a) - t(b)$なので、$t(a)$の値と$t(b)$の値が決まれば$t(c)$の値が決まります。
つまり、$t_1, t_2 \in R_1$に対して、$(t_1(a), t_1(b)) = (t_2(a), t_2(b))$ならば、$t_1(c) = t_2(c)$が言えます。すなわち、$\set{a,b}\to \set{c}$が成り立ちます。
同様に、$\set{b,c}\to \set{a}$や$\set{c,a}\to \set{b}$も言えます。また、$\set{a,b}\to \set{a,b,c}(=P_1)$も言えます。
さらに、自明な関数従属性として、$\set{a}\to \set{a}, \set{a,b}\to \set{a}, \set{a}\to \emptyset, \emptyset \to \emptyset$ なども言えます(「自明な」というのは$R_1$の定義を見なくても属性だけを見れば言えるということです。)
次に関数従属性が成り立たない例を見ていきます。$\set{a}\to \set{b}$は成り立ちません。$t_1, t_2\in R_1$を$(t_1(a), t_1(b), t_1(c)) = (1,0,2), (t_2(a), t_2(b), t_2(c)) = (1,1,1)$で定義すると、$t_1(a) = t_2(a)$ですが、$t_1(b)\neq t_2(b)$です。つまり$\set{a}\to \set{b}$は成り立ちません。
次に関数従属性の性質を見ていきます。
$\langle P, D, R\rangle$を関係データモデルとします。このとき次の性質が成り立ちます。
- 反射律: 任意の$X\subseteq P$に対して$X\to X$が成り立つ。
- 推移律: 任意の$X,Y,Z\subseteq P$に対して$X\to Y$かつ$Y\to Z$ならば$X\to Z$が成り立つ。
要するに$(2^P, \to)$は 前順序集合 ということです。
証明は簡単なので省略します。
反対称律($X\to Y$かつ$Y\to X$ならば$X=Y$)は成り立つとは限りません。
$P_3 = \set{a,b}$、$D_3(A) = \set{0,1}\ (A\in P_3)$、$R_3=\setsep{t\in \prod_{A\in P_3}D_3(A)}{t(a) = t(b)}$とし、
$\langle P_3, D_3, R_3\rangle$の関係データモデルを考えます。
| $a$ | $b$ |
|---|---|
| 0 | 0 |
| 1 | 1 |
このとき、$\set{a}\to \set{b}$、$\set{b}\to \set{a}$ですが、$\set{a}\neq \set{b}$です。
つまり、反対称律は成り立つとは限りません。
$\langle P, D, R\rangle$を関係データモデルとします。このとき次の性質が成り立ちます。
- $X,Y\subseteq P$について、$Y\subseteq X$が成り立つならば$X\to Y$が成り立つ。
- $X,Y,Z\subseteq P$について、$X\to Y$が成り立つならば$X\cup Z\to Y\cup Z$が成り立つ。
1つめのは反射律の一般化です。
命題1の推移律と命題2の2つの性質をあわせてアームストロングの規則と言うそうです( Wikipediaの関数従属性 )。
$\langle P, D, R\rangle$を関係データモデルとします。このとき次の性質が成り立ちます。
- $X,Y,Z\subseteq P$について、$Y\subseteq X$かつ$Y\to Z$ならば$X\to Z$
- $X,Y,Z\subseteq P$について、$Z\subseteq Y$かつ$X\to Y$ならば$X\to Z$
この系は推移律の特殊バージョンです。
完全関数従属性
関数従属性より強い概念である完全関数従属性を定義します。
$\langle P, D, R\rangle$を関係データモデルとします。
2つの属性の集合$X,Y\subseteq P$について、$X$が$\setsep{X'\subseteq P}{X'\to Y}$の(集合の包含関係による)極小元であるとき、$Y$は$X$に完全関数従属していると言います。
言い換えると、$X\to Y$だが、任意の$X'\subsetneq X$に対して$X'\to Y$ではないとき、$Y$は$X$に完全関数従属していると言います。
極小元であるというのは、$Y$に属している属性の値をすべて決めるのに$X$の中に無駄な属性が無い($X$から一つでも属性が欠けたら$Y$に属している属性の値をすべて決めるということができない)ということです。
$X\to Y$が完全関数従属性であることを確認するためには、「任意の$x\in X$に対して、$X\setminus\set{x}\to Y$でない」ことを確認すれば十分です。
$P_4 = \set{a,b,c}$、$D_4(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_4)$、$R_4=\setsep{t\in \prod_{A\in P_4}D_4(A)}{1\leq t(a)\leq 3, 1\leq t(b)\leq 3, t(c) = \lfloor (t(a)+ t(b) )/2\rfloor}$
で定義される関係データモデル$\langle P_4, D_4, R_4\rangle$について考えます。
| $a$ | $b$ | $c$ |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 2 | 1 | 1 |
| 2 | 2 | 2 |
| 2 | 3 | 2 |
| 3 | 1 | 2 |
| 3 | 2 | 2 |
| 3 | 3 | 3 |
$\set{c}$は$\set{a,b}$に関数従属します(つまり、$\set{a,b}\to \set{c}$が成り立ちます)。さらに、$\set{c}$は$\set{a,b}$に完全関数従属します。完全関数従属することを見ていきます。
$\set{a}\to \set{c}$や$\set{b}\to\set{c}$は成り立ちません(もちろん$\emptyset\to \set{c}$も成り立ちません)。よって、$\set{c}$は$\set{a,b}$に完全関数従属します。
$P_5 = \set{a,b,c}$、$D_5(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_5)$、$R_5=\setsep{t\in \prod_{A\in P_5}D_5(A)}{1\leq t(a)\leq 3, 1\leq t(b)\leq 3, t(c) = \lfloor t(b)/2\rfloor}$
で定義される関係データモデル$\langle P_5, D_5, R_5\rangle$について考えます。
$\set{c}$は$\set{a,b}$に関数従属します(つまり、$\set{a,b}\to \set{c}$が成り立ちます)。一方、$\set{c}$は$\set{a,b}$に完全関数従属はしません。$\set{b}\to \set{c}$だからです。
「$\set{c}$は$\set{a,b}$に関数従属する」と言うのに、属性$a$は冗長(属性$a$の値がなくても属性$c$の値が定まる)なので、完全ではないということです。
キー
タプルを特定する場合に、一部の属性の値だけがわかればいい場合があります。
どの属性の値を知ればいいかという議論にスーパーキーやキー候補といった概念が出てきます。
$\langle P, D, R\rangle$を関係データモデルとします。
$K\subseteq P$が$K\to P$を満たすとき、$K$をスーパーキーと言います。
スーパーキー$K$に属する属性の値がわかればタプルが一意に特定できます。特に、$P$はスーパーキーです。
$\langle P, D, R\rangle$を関係データモデルとします。
$K\subseteq P$について、$P$が$K$に完全関数従属しているとき、$K$をキー候補と言います。
別の言い方をすると、スーパーキー全体の集合の極小元をキー候補と言います。
キー候補は「ほしいタプルを特定するための無駄のない属性の集合」といえます。
キー候補は必ず1つは存在します($P$がスーパーキーなので)。ただし、キー候補が複数ある場合もあります(極小元が1つとは限らないので)。
$P_1 = \set{a,b,c}$、$D_1(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_1)$、$R_1=\setsep{t\in \prod_{A\in P_1}D_1(A)}{t(a) + t(b) + t(c) =3}$
で定義される、関係データモデル$\langle P_1, D_1, R_1\rangle$のスーパーキーやキー候補を考えます。
例5で見たように、$\set{a,b}\to \set{c},\set{b,c}\to \set{a},\set{c,a}\to \set{b}$が成り立ちます。関数従属性の各種性質から、$\set{a,b}\to P_1, \set{b,c}\to P_1, \set{c,a}\to P_1$が成り立ちます。よって、$\set{a,b}, \set{b,c}, \set{c,a}$はスーパーキーです。$\set{a,b}$から属性を一つ取るとスーパーキーではなくなる($\set{a}\to P_1$と$\set{b}\to P_1$は成り立たない)ので、$\set{a,b}$はキー候補です。同様に$\set{b,c}, \set{c,a}$もキー候補です。
$P_1\to P_1$なので$P_1$はスーパーキーですが、$\set{a,b} \subsetneq P_1$もスーパーキーなので、$P_1$はキー候補ではないです。
$P_6 = \set{a,b,c}$、$D_6(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_6)$、$R_6=\setsep{t\in \prod_{A\in P_6}D_6(A)}{t(a)\leq 3, t(b)\leq 3,t(c)\leq 3}$
で定義される、関係データモデル$\langle P_6, D_6, R_6\rangle$のスーパーキーやキー候補を考えます。
属性$a,b,c$は独立しているので、$\set{a,b}\to \set{c}$などが成り立たず、$P_6=\set{a,b,c}$が唯一のスーパーキーです。つまり、$P_6=\set{a,b,c}$が唯一のキー候補です。
関係データモデル$\langle P, D, R\rangle$で、$\abs{R}\leq 1$の場合(つまりタプルがまだ1つしか入っていないか、1つも入っていない場合)を考えます。
関数従属性の定義から、任意の$X,Y\subseteq P$に対して、$X\to Y$が言えます。特に$\emptyset \to P$が言えます。つまり、$\emptyset$はスーパーキーで唯一のキー候補です。これは、属性が一つも決まらなくてもすべての属性の値が決まる(タプルが特定できる)ということです(タプルが1つ以下なので当たり前ですが)。
このように、タプル数が少ない場合に関数従属性やキーの話をするのは意味がないです。
第2正規形(2NF)
最後に関係データモデルで重要な概念であると思われる正規形、とくに第2正規形(2NF)の定義を定式的に与えたいと思います。
$\langle P, D, R\rangle$を関係データモデルとします。$\mathcal{K}$を候補キー全体の集合とします。
$A\in P$について、任意の$K\in \mathcal{K}$に対して、$A\notin K$であるとき、$A$を非キー属性といいます。
つまり、$(\bigcup_{K\in \mathcal{K}}K)^C$の元を非キー属性といいます。
$\langle P, D, R\rangle$を関係データモデルとします。$\mathcal{K}$を候補キー全体の集合とします。
任意の非キー属性$A$、任意の$K\in \mathcal{K}$に対して、$\set{A}$が$K$に完全関数従属するとき、この関係データモデルは第2正規形(2NF, 2nd Normal Form)であるといいます。
$K\in \mathcal{K}$に対して、$K\to P$なので常に$K\to \set{A}$つまり$\set{A}$は$K$に関数従属します。よって完全であるかどうか(つまり$\set{A}$が$K$の真部分集合に関数従属しないかどうか)が2NFの定義では重要になります。
$P_4 = \set{a,b,c}$、$D_4(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_4)$、$R_4=\setsep{t\in \prod_{A\in P_4}D_4(A)}{1\leq t(a)\leq 3, 1\leq t(b)\leq 3, t(c) = \lfloor (t(a)+ t(b) )/2\rfloor}$
で定義される関係データモデル$\langle P_4, D_4, R_4\rangle$は2NFです。2NFであることを見ていきます。
| $a$ | $b$ | $c$ |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 2 | 1 | 1 |
| 2 | 2 | 2 |
| 2 | 3 | 2 |
| 3 | 1 | 2 |
| 3 | 2 | 2 |
| 3 | 3 | 3 |
$\set{a,b}\to \set{c}$は成り立ちます。一方、$\set{a}\to \set{b}$や$\set{b}\to\set{a}$、$\set{b,c}\to \set{a}$、$\set{c,a}\to \set{b}$は成り立ちません。
関数従属性から、候補キーは$\set{a,b}$のみであることがわかります。また、非キー属性は$c$のみです。
なお、関数従属性を図に表すと次のようになります。
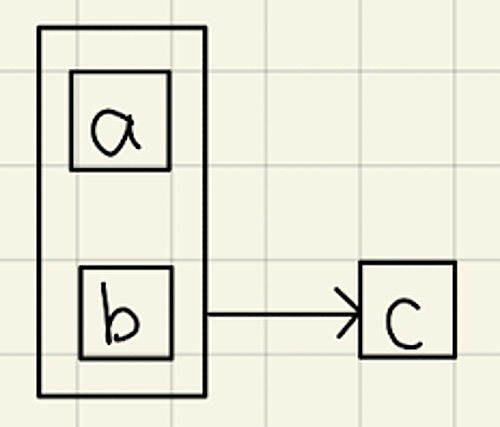 FD1
FD1
ここで、$\set{c}$は$\set{a,b}$に完全関数従属しています($\set{a,b}\to \set{c}$は成り立っているが、$\set{a}\to \set{c}$や$\set{b}\to \set{c}$は成り立っていないので)。
以上から関係データモデル$\langle P_4, D_4, R_4\rangle$は2NFであることが言えます。
$P_5 = \set{a,b,c}$、$D_5(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_5)$、$R_5=\setsep{t\in \prod_{A\in P_5}D_5(A)}{1\leq t(a)\leq 3, 1\leq t(b)\leq 3, t(c) = \lfloor t(b)/2\rfloor}$
で定義される関係データモデル$\langle P_5, D_5, R_5\rangle$は2NFではないです。2NFでないことを見ていきます。
$\set{b}\to \set{c}$が成り立ちます。よって、$\set{a,b}\to \set{c}$や$\set{a,b}\to P_5$が成り立ちます。つまり、$\set{a,b}$はスーパーキーです。
一方、$P_5$と$\set{a,b}$以外の属性の集合($\set{b,c}$と$\set{c,a}$とそれらの部分集合)はスーパーキーではないです。
よって、キー候補は$\set{a,b}$のみです。また、非キー属性は$c$のみです。
なお、関数従属性を図に表すと次のようになります。
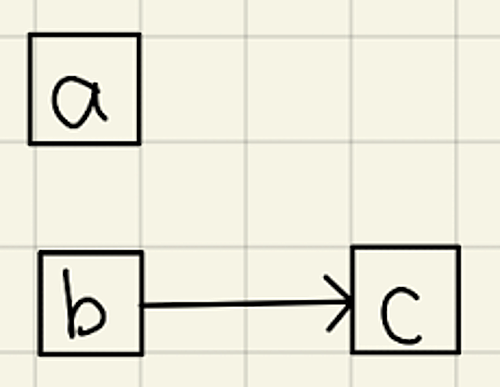 FD2
FD2
非キー属性$c$について、$\set{c}$はキー候補$\set{a,b}$に完全関数従属しません。なぜならば、$\set{b}\to \set{c}$が成り立つからです。
以上から、$\langle P_5, D_5, R_5\rangle$は2NFではないです。
$P_7 = \set{a,b,c}$、$D_7(A) = \setsep{n\in \Z}{n\geq 0}\ (A\in P_7)$、$R_7=\setsep{t\in \prod_{A\in P_7}D_7(A)}{1\leq t(a)\leq 3, 1\leq t(b)\leq 3, t(c) = t(b)}$
で定義される関係データモデル$\langle P_7, D_7, R_7\rangle$は2NFです。
$\set{b}\to \set{c}$や$\set{b}\to \set{a}$が成り立ちます。
関数従属性を図に表すと次のようになり、キー候補は$\set{a,b}, \set{a,c}$です。
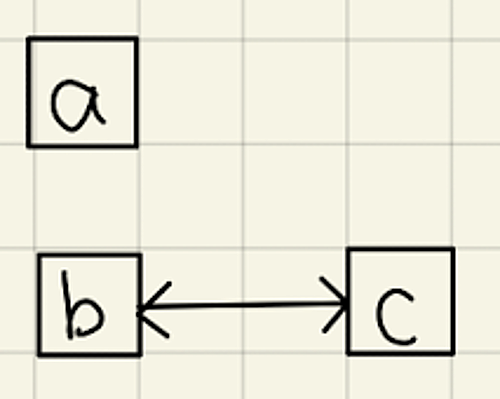 FD3
FD3
非キー属性は存在しないので$\langle P_7, D_7, R_7\rangle$は2NFです。
2NFの定義「任意の非キー属性$A$、任意の$K\in \mathcal{K}$に対して、$\set{A}$が$K$に完全関数従属する」で$A$を非キー属性に限定していますが、この例では$A$を非キー属性に限定していることが有効にはたらいています。というのは「任意の非キー属性$A$、任意の$K\in \mathcal{K}$に対して、$\set{A}$が$K$に完全関数従属する」は真だが、「任意の属性$A$、任意の$K\in \mathcal{K}$に対して、$\set{A}$が$K$に完全関数従属する」は偽となる例になっているからです。
例えば$\set{c}$はキー候補$\set{a,b}$に(関数従属しているが)完全関数従属していないです($\set{b}\to \set{c}$なので)。よって、「任意の属性$A$、任意の$K\in \mathcal{K}$に対して、$\set{A}$が$K$に完全関数従属する」は偽です。
おわりに
この記事では、集合論をベースに関係データモデルの定義から関数従属性、キー、2NFの定義を定式化し、その定義を満たす例と満たさない例をいくつか与えました。わかりやすさはともかく、(同内容の他の解説と比べて)数学的に厳密な定義は与えられたかと思います。
他の関係データモデルの解説にはあまりないこの記事の特徴としては、タプルを写像として与えたこと、タプルの複数の属性の値の取得に写像の制限を用いたことが挙げられます。
この記事を書いてて、集合論はなにかを記述する言語として便利だなぁと思いました。
補足
この記事では関数従属性を満たすかどうかをタプルを見て決めていますが、そもそも現実では、タプルを見て決まるものというよりかは、この関数従属性を満たすタプルしか入らないというのが正しい見方のような気がします。タプルを見て関数従属性を考えると、タプル数が少ない場合に例10のような意味のない議論が発生してしまいます。現実世界でいうと、属性として(ユニークな)IDと本名を持つ関係データベースを考えた場合、{ID}→{本名}と{本名}→{ID}と両方向の関数従属性が見えるかもしれませんが、もしかしたら今後同姓同名の人が登録して{本名}→{ID}の関数従属性が満たされなくなるかもしれません。タプルを見て関数従属性を決めると関係の状態に大きく左右されてしまいます。
そこで、関係(タプルの中身)によらずに関数従属性を定義したいです。ありえる関係をすべて集めた関係の集合$\mathcal{R}\subseteq 2^{\prod_{A\in P}D(A)}$ を定義し($R\in \mathcal{R}$が関係の一例です。)、$\langle P, D, \mathcal{R}\rangle$ に対して関数従属性を定義してあげるという方法がありそうです($\langle P, D, R\rangle$が関係データベースの実際のデータなのに対して、$\langle P, D, \mathcal{R}\rangle$は関係データベースの設計に当たります)。具体的には$X, Y \subseteq P$に対して、$X\to Y$を「任意の$R\in \mathcal{R},\ t_1, t_2\in R$に対して、$t_1|_X = t_2|_X$ならば$t_1|_Y = t_2|_Y$」と定義してあげればよさそうです。
この関数従属性の定義は
関西学院大学のデータベース論の講義資料
を参考にしました(この講義資料では$R\in \mathcal{R}$をインスタンスと呼んでいます)。
最後に$\langle P, D, \mathcal{R}\rangle$の具体例をあげて終わりにしたいと思います。$P=\set{a,b}$で、属性$a$に一意性制約(2つの異なるタプルで属性$a$の値が等しいものが存在しないようにする制約)があるとします。このとき、
$\mathcal{R} = \setsep{R \subseteq \prod_{A\in P}D(A)}{\forall t_1, t_2\in R, t_1(a) = t_2(a) \Rightarrow t_1 = t_2}$
と書けます。このとき、$\langle P, D, \mathcal{R}\rangle$において関数従属性$\set{a}\to P$が成り立ちます。
