世界二難しい論理パズル(?)の類題と、削除符号。
皆さん!こんにちは!
IE50_testさんの
全国の多変数関数にお悩みの大学生を救う記事
に続き
2020年
日曜数学
アドベントカレンダー7日目の記事です!
ええ、そうです!私は、あのとき助けて頂いたキジです!
最近は、きびだんごを巡ってイヌとサルの喧嘩が終わらずに困ってます!
このたびは恩を返しにやって参りました!
 kijinoongaeshi
kijinoongaeshi
${\LARGE いやそれ鶴やないかーーーーーーい!!}$
$$ $$
${\large \cdots いや雉が恩を返したっていい!!そうだろう?}$
えー、ぺこぱはさておき今回はある論理パズルと、ある符号の二本立てでお送りしたいと思います!
${\textcolor{red}{世界一}}$難しい論理パズル(The Hardest Logic Puzzle Ever)といえば、 三神の問題 ですが、今回は それに匹敵する難易度と言われるチェス盤のパズル の類題を考えました!
専門的な知識が無いと解けないということが無いように、後半で削除符号というものについての解説をしますが、まずはぜひ解説を読まずに挑戦してみて下さい!その際、類題の元ととなったパズルの解法を知らなくても全く問題ありません!
悪魔が告げた数字は?
 puzzle!!
puzzle!!
表裏を気にせずにシャッフルされた52(=13×4)枚のトランプがある。まず、悪魔は囚人Aだけに1~54の数字を一つ告げる。
その数字を聞いて、囚人Aは黒のジョーカーを表か裏にしてトランプの上から何番目かに必ず挿入する。(もちろん一番上に置いてもよい。)
その後、囚人Bはそのトランプの状態を見て、赤のジョーカーを好きな位置に必ず挿入する。
囚人A,Bはトランプに対して、ジョーカーを挿入することと広げる(スプレッドする)$^*$こと以外の行為(カードをめくる等)はやってはいけない。
最後に、悪魔がカードを上から順番に(1枚目,2枚目,...,54枚目のように)引いていく。悪魔が告げた数字番目に赤のジョーカーを引けば、囚人達の勝利となる。
囚人達はこのゲームを始める前に戦略を練ることが出来る。この際トランプの初期状態は知らされない。さて、囚人達はどのような戦略を取ればいいか?
ここでトランプをスプレッドするとは、以下のように順番を崩さずにトランプを広げることを指します。(図中のハートのエースは問題文中でいう赤のジョーカー)
 spreadnozu
spreadnozu
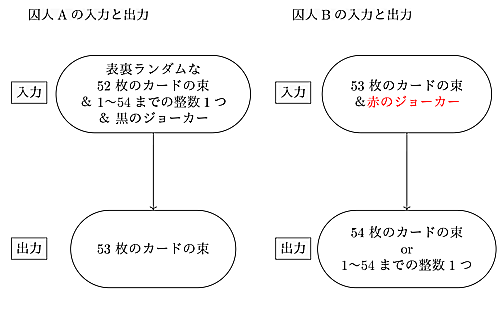
この問題における囚人A、囚人Bそれぞれにおける入力と出力は以下のフローチャートの通りです。(入力で得られるのは正確にはスプレッドで得られるトランプの情報。)
 inputoutput
inputoutput
しかし一見すると難しくなさそうな(?)このゲーム、悪魔の罠が潜んでいたようで$\cdots$
囚人A(なぁんだ$\cdots$悪魔が言った数字番目に、黒のジョーカーを表向きに挿入して囚人Bには赤のジョーカーを上に重ねてもらえればいいじゃん!)
囚人A(黒のジョーカーが見つからなかったら最後(54番目)ってことにすればいいんだし!)
囚人A「ようし!そのゲーム乗った!!」
囚人B「いや...待て!何か嫌な予感がする...。」
悪魔「${\bf 参加を宣言したな}$...それではゲーム開始だ...!!」
悪魔「ちなみに君達がゲームに参加するか否かを迷っている間に残念だがトランプの絵柄(表の面)のインクが飛んでしまったようだ.」
悪魔「黒のジョーカーも例外じゃない.囚人A,君は表と裏しかないただのカードの束に対して,表と裏しかないただのカードを挿入することになる.」
囚人A「何だと...!?」
悪魔「俺もあくまで悪魔であって,鬼じゃない.赤のジョーカーだけは特殊なインクが使われているから絵柄は残っている.せいぜい頑張ってくれたまえ.アヒャヒャヒャヒャ!!」
囚人B「$\cdots$そんな予感はしていたさ。悪魔、お前の負けだ。このゲームには必勝法がある...!!(流れ出す Electrode Sprak 0101 )」
悪魔「Nani!?」
・・・あくまで悪魔の悪魔なゲームに参加してしまった囚人達でしたが、ここで皆様にお伝えしたいことがございます。
なんと囚人達はインクが飛んでしまった状態のトランプでも勝利出来る戦略を立てたため、ゲームに勝てたそうです!
さて、どのような戦略だったのでしょうか!?
いきなり52枚の裏表しかない(インクが飛んだ)カードの束を扱うのは難しいので例としてカードの束が1枚で、悪魔が言う数字が1~3の場合を考えてみましょう。
 omoteura
omoteura
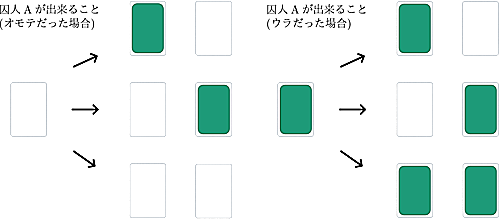
カードの束の初期状態は、1枚しかないのでオモテかウラかです。
どちらの状態であっても囚人Aは1枚のカードを挿入することで3通りの状態を作れます。この3通りの状態を整合的に1~3の数字に対応させる解釈の仕方を考えれば、囚人Bに悪魔が言った数字を伝えることが出来ます。これは上図で上から1,2,3と解釈するとよさそうです。つまり、
2枚のカードの束のウラオモテが揃っていないとき、
1枚目がウラであれば1、2枚目がウラだったら2と解釈することにし、
2枚のカードの束のウラオモテが揃っているとき、3と解釈することにすれば、
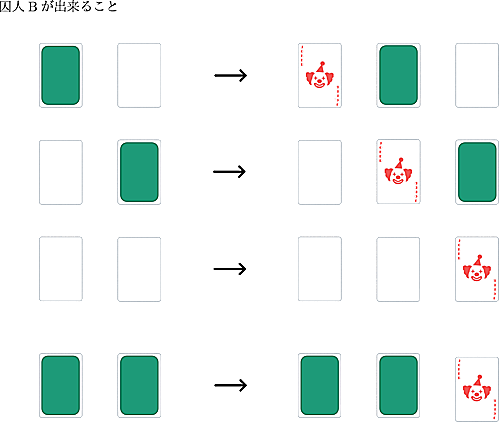
囚人Aは囚人Bに悪魔が言った数字を伝えられ、囚人Bは悪魔が言った数字を当てることが出来ます。
数字が分かった為、その数字番目に赤のジョーカーを挿入すれば勝利です!
 joker_trump
joker_trump
元々のカードの束が1枚だったときは勝てました!では元々のカードの束が2枚、3枚、、、52枚だったら...どうでしょう?
削除符号について
ここから上記のパズルの解法につながる削除符号というものを紹介します。
実は、削除符号は次世代の情報記録媒体であるDNAデータストレージに使われる符号(仕組み)だったりします。
DNAデータストレージとは、その名の通りDNAを用いたデータ$\stackrel{ストレージ}{記録媒体}$のことで、1gあたり215PB(ペタバイト)の情報を数十万年保存出来ると言われており、近い未来に訪れる情報爆発を解決する手段として期待されています。 (これで一万年と二千年前からア・イ・シ・テ・ルのサインも一安心。一億と二千年たったブレーキランプはfuture works。)
削除符号はこの他にも面白い話題がある為、あえてパズルとのつながりには触れずに紹介します!しかし、いつの間にかパズルのヒントになっているように紹介します!
まず、そもそも符号とは?符号理論とは?という所から始めます。
大ざっぱに
符号理論
(誤り検出訂正)とは、コミュニケーションの際にメッセージが間違って伝わったとしても、ある程度なら正しく推測出来るような伝え方、もしくは間違って伝わったことが分かるような伝え方を考える理論です。この伝え方のことを符号化(encode)、推測の仕方のことを復号(decode)といいます。
この符号化と復号の組を符号と呼ぶこともありますが、今回はある程度間違って伝わっても正しく推測出来るような構造を持つメッセージの集合(空間)のことを符号と呼びます。
符号理論はCDや主記憶装置、QRコードなどメッセージのやり取りを行う様々な場面で実際に使われていて、最近では量子コンピュータに用いられる量子誤り訂正符号も研究されています。工学的なアプローチも数学的アプローチ(組み合わせ論、デザインなど)もある研究対象です。
ちなみに
オンライン整数列大辞典(OEIS)
の創設者
N.J.A Sloane
は符号理論の研究者です。
例として"ありがとう"、"ごめんなさい"、"さようなら"というメッセージを、ある程度間違って伝わっても正しく推測出来るように
$$\text{"ありがとう Thank you Obrigada Grazie 謝謝", }\\
\text{"ごめんなさい Sorry Lo siento Mi dispiace 対不起" }\\
\text{"さようなら Good bye Adios Ciao 再見"}$$
と様々な国の言葉も付け加えて言うことにしましょう。(符号化)
そうするとこのうちの一つが、急に鳴った雷の音で一部聞こえなかったり、そもそも喉や口の調子が悪かったりで、
$$\text{"ざ?%你a rGoo...くぁwせdrftgyふじこ lp}\cdots\text{iao 再見"}$$
と伝わったとしても、$\text{"さようなら"}$かな?と推測出来ることでしょう。(復号)
NICO Touches the Walls大勝利!!(
手をたたけ
)
(この3つのメッセージだけでも告白の返事は出来そうなので
ボッコちゃん
に実装するといいかもしれません。${\color{white} また客が死ぬ。}$)
半ば無理矢理な例でしたが、一般にメッセージが冗長に(やたら長く)なってしまうことが問題になります。そこで、発生しやすい間違った伝わり方(誤り)に特化した冗長性、構造を持ったメッセージの集合(符号)を考えることになります。ではそもそも誤りとはどのようなものが考えられるでしょうか?
以下が基本的な誤りの例です。このうちの削除誤り、が起きても訂正出来る集合を削除符号と呼びます。
$$ 10110 \stackrel{一文字反転}{→} 1{\color{red}1}110 \,\ 10110 \stackrel{一文字消失}{→} 1{\color{red} ?}110 \\ 10110 \stackrel{一文字削除}{→} 1010 \quad 10110 \stackrel{一文字挿入}{→} 101110 $$
削除(挿入)誤りの特徴は、何番目が削除(挿入)されたかは最後まで分からないことがあるという点です。そんな状況を体感出来る例が身近にあります。だるま落としです。
 daruma
daruma
$$ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \color{red}{\text{SMASH!!!}} $$
 daruma3
daruma3
たったいま${\color{green}緑色}$と${\color{skyblue }水色}$のブロックが積まれていたなかで、${\color{green}緑色}$のブロックが飛ばされて(削除されて)しまいました。
しかし、上から何番目のブロックだったかは分かりません。上から3番目の${\color{green}緑色}$のブロックかもしれませんし、4番目の${\color{green}緑色}$のブロックだったのかもしれません。
このように何番目かのブロックにあたるものが無くなってしまったとき、空白は残らずに間が詰まるような場面でこのような状況になります。
(そうでない状況の例として、指定席の試験は欠席者が出たときに前から何番目に欠席が出たか分かります。これは消失誤りに対応します。)
筆者自身詳しくは分からないですが、4種類の塩基ATGC(アデニン、チミン、グアニン、シトシン)からなるDNAの塩基配列を扱う際に削除や挿入が起きるようです。CTCGAGAGTA$\cdots\rightarrow$CTCGGGG$\cdots$など。
では削除誤りが起きても誤りが訂正出来て(削除符号であって)、数学的に扱いやすいものはどのようなものがあるのでしょう??
その一つが以下のある合同式によって定まるVT符号です。(VTとは、発見者であるVarshamovとTenengoltsの名からとられています。)
自然数は$1$以上の整数のこととします。
$n:$自然数, $a:$整数に対して、集合${\text{VT}}_a(n)$を以下で定める。
$${\text{VT}}_a(n) \\
:=\{(x_1,x_2,\cdots, x_n)\in\{0,1\}^n\mid 1x_1+2x_2+\cdots+nx_n\equiv a \pmod {n+1} \} $$
この集合を符号長$n$,パラメータ$a$のVT符号と呼ぶ。
長さ$n$のビット列($0$と$1$からなる系列)で、$1$から$n$までの自然数の列との(標準)内積をとり、その値を$n+1$で割った余りが$a$になるもの全体の集合がVT符号です。一文字の削除誤りに耐性があります。(実は挿入も)
$a=0$であれば、それぞれ1コずつ用意された$1$~$n$$\text{g}$の分銅を用いて$(n+1\text{の倍数})$$\text{g}$の重さを作るときの、分銅の選び方$(x_1,x_2,\cdots, x_n)$の集合とも言えます。
 hundou
hundou
各$x_i$は$0$か$1$かですので、$i$$\text{g}$の分銅を使うか使わないかに対応します。($1\leq i \leq n$)
また、この$0$と$1$は二元体$\mathbb{F}_2$の元ではなく整数の$0,1$です。要するに$1+1=0$ではなく、$1+1=2$です。(そらそうだ)
(ちなみにVT符号の元の個数として、数列$|{\text{VT}}_0(n)|$はOEIS A000016 (番号が若い!)、数表(?)$|{\text{VT}}_k(n)|$はOEIS A053633 に載っています。)
符号長$4$,パラメータ$0$の例を見てみましょう。
$${\text{VT}}_0(4)=\{(x_1,x_2,x_3,x_4)\in\{0,1\}^4\mid 1x_1+2x_2+3x_3+4x_4\equiv 0 \pmod {5} \} \\
=\{0000,0110,1001,1111\} $$
($0000$は$(0,0,0,0)$の略記です。)
(例が悪いのですが、一般には線形性は成り立ちません。だって$1+1=2$だから!)
長さ$4$のビット列$(x_1,x_2,x_3,x_4)$で、自然数列$(1,2,3,4)$と内積をとり、その値を$5$で割った余りが$0$になるビット列全体の集合が$\text{VT}_0(4)$です。
実際に
$$1\cdot{\color{red} 0}+2\cdot{\color{red} 0}+3\cdot{\color{red} 0}+4\cdot{\color{red} 0}=0\\
1\cdot{\color{red} 0}+2\cdot{\color{red} 1}+3\cdot{\color{red} 1}+4\cdot{\color{red} 0}=5\\
1\cdot{\color{red} 1}+2\cdot{\color{red} 0}+3\cdot{\color{red} 0}+4\cdot{\color{red} 1}=5 \\
1\cdot{\color{red} 1}+2\cdot{\color{red} 1}+3\cdot{\color{red} 1}+4\cdot{\color{red} 1}=10 $$
であり、これらの値を$5$で割った余りは$0$となっています。
ここで、VT符号の元(符号語と呼ぶ)それぞれに対して削除誤りが起こるとどうなるかを見てみます。
$0000\rightarrow 000$ (どこを削除されたかに関わらず,削除しても一人。)
$0110\rightarrow 110,010,011$ (削除のされ方によって$3$通りの系列が現れる。)
$1001\rightarrow 001,101,001$ (1つ上に同じ。)
$1111\rightarrow 111$ (3つ上に同じ。)
ここで削除後の系列に被りはありません!そのため、削除後の系列から一意的に元の符号語を推定することが出来ます!
また、削除後の系列をよーく見ると、$000$から$111$まで長さ$3$のビット列が全て現れていることが分かります!
($0$~$7$までの$2$進表記が全て現れているとも言えます。)
つまり、長さ$3$のビット列全体をVT符号の各符号語を基準に分類する(=直和分割する)ことが出来るということです。
$$\{0,1\}^3 \\ =(0000\text{産だよ)}\cup(0110\text{産です})\cup(1001\text{産やで})\cup(1111\text{産!}) \\ =\{000\}\cup\{110,010,011\}\cup\{001,101,100\}\cup\{111\}$$
例えばビット列$110$は符号語$0110$からきた(一文字削除された)ものと分類されます。このように長さ$3$のビット列は全て、どの符号語からくるかという基準で分類することが出来ます。
あなたの符号語はどこから? 私は$1111$から!
という会話があれば$111$が答えていることが分かりますね!
うわっ$\cdots$私の直感、冴えすぎ$\cdots$??
さらに驚くべきことに、このVT符号の性質(どの符号語からくるかという基準で、長さが$1$短いビット列全体の分類を与える性質)は、任意の符号長$n$と任意の整数$a$において成り立ちます。
つまりVT符号${\text{VT}}_a(n)$は符号長$n$やパラメータ$a$によらずに上記の性質をもつということです。
例えば、${\text{VT}}_{12}(8)(={\text{VT}}_{3}(8))$の各符号語から一文字削除して得られる系列全体の集合達は、長さが$7$のビット列全体($0000000$~$1111111$まで$2^7={\color {red}128}$個ある)の直和分割を与えます!
架空のアイドルグループ$\text{ZiuNi}$($={\text{VT}_{12}(8)}$)のメンバーの誰を担当する(誰推し)かでファン達($=$長さ$7$のビット列全体)がきっちり分かれる様子が見えますね!(例3の分類基準 お前、どこ産?が お主、どこ担?になっただけです!)
今日の日付である12/8的にもいい感じの話題になりました!(強引)
最後にこの性質を数学的に定式化しておきます。
任意の自然数$n$と任意の整数$a$に対して、
$$\{0,1\}^{n-1}=\bigcup_{{\bf x}\in{\text{VT}_a(n)}} \text{dS}({\bf x}) $$
かつ、相異なる符号語${\bf x},{\bf x'}\in \text{VT}_a(n)$に対して、
$$ \text{dS}({\bf x}) \cap \text{dS}({\bf x'})=\emptyset$$
が成り立つ。ただし、$\text{dS}({\bf x})$はビット列${\bf x}$から一文字削除して得られる系列全体の集合(=削除球面(deletion sphere))を表す。
このことをVT符号は単一削除誤りに対して完全であると言います。(符号長やパラメータに依存しない。)
論理パズルに繋がるように、このことを更に言いかえていきます。
和集合と部分集合($ \subset$)の定義から、任意のビット列${\bf y}\in \{0,1\}^{n-1}$に対して、ある符号語${\bf x} \in \text{VT}_a(n)$が存在して、${\bf y} \in \text{dS}({\bf x})$(${\bf y}$は${\bf x}$から一文字削除されたものである)が成り立つことが分かります。
どんなビット列${\bf y}\in \{0,1\}^{n-1}$も何かしらの符号語${\bf x} \in \text{VT}_a(n)$から一文字削除されたものになるということです。
また削除球面$\text{dS}({\bf x})$達は、共通部分を持たないため、上記の和集合は直和であり、${\bf y} \in \text{dS}({\bf x})$なる符号語${\bf x}$の存在は一意的であることが分かります。
ビット列${\bf y}\in \{0,1\}^{n-1}$は運命の符号語${\bf x}\in \text{VT}_a(n)$から一文字削除されたものになるぞということです。
ここで$\text{iS}({\bf y})$をビット列${\bf y}$に$0$か$1$の一文字を挿入して得られる系列全体の集合(=挿入球面(insertion sphere))とすると、ビット列${\bf x},{\bf y}$に対して、
${\bf y} \in \text{dS}({\bf x})$(${\bf y}$は${\bf x}$から一文字削除されたもの)であることと、
${\bf x} \in \text{iS}({\bf y})$(${\bf x}$は${\bf y}$から一文字挿入されたもの)であることは同値です。
${\bf x}$から${\bf y}$に一文字削除でたどり着いたなら、${\bf y}$から${\bf x}$へは一文字挿入でいけるよねということです。
以上から次の系が言えます。
任意の自然数$n$と任意の整数$a$と任意のビット列${\bf y}\in \{0,1\}^{n-1}$に対して、${\bf y}$に一文字挿入して得られる符号語${\bf x}\in\text{VT}_a(n)$は一意的に決まり、必ず存在する。
要するにビット列${\bf y}$から一文字挿入でいける符号語${\bf x}$は運命の赤い糸によって一つに決まっていて現世に生きているということです。
(ちなみに${\bf y}$にとって${\bf x}$は唯一無二の存在だけど、${\bf x}$にとっての${\bf y}$はその他大勢のうちの一人。つらたん。)
(それでも$n=53$とするといいことあるかもしれません。)
おわりに
さて難問論理パズルと削除符号の話はここまでで終わりです!
いかがでしたでしょうか?
実はVT符号の完全性を使うことで、あと1歩でパズルを解くことが出来ます!
解答編は12/22の日曜数学アドベントカレンダー
21日目の記事
にて公開いたしますのでお楽しみに!!
(結局のところ、VT符号の完全性の面白さを伝える為に論理パズルや、その他の例、小ネタを書いたまでありました。
伝えたいことを誤解なく伝えるために色々な冗長性(冗談性)を付け加える、まさにこのブログ記事が符号理論...(?) ${\color{white}ふご~!}$)
明日はキグロさんの
ネジの山の形について
です!
$\,\,\,$共通内接線、引けますか!
