論理パズルの解説と、ハミング符号。
こんにちは！ヘカテーと申します！院生をやっています！
楕円曲線の群構造の概要が学べる前日のRyuさんによる記事、
楕円曲線論への誘い～ロマ数トレラン受講記録～
に引き続き、2020年
日曜数学
アドベントカレンダー２１日目の記事です！
年の瀬は早いものでクリスマス(アドカレ最終日)まで残り４日になる１２／２２今日この頃ですが、"毎月２２日はショートケーキの日"と国内のケーキ屋さんで呼ばれていることを皆様ご存じですか？
layered_cake
その理由はカレンダーにありまして、２２日の一週間前が１５日であるため、カレンダー上でちょうど２２日の真上に１５日(イチゴ)が乗っている形になるからだそうです！面白い！
この理屈でいくと一週間後は２９日(肉の日)なので、イチゴと肉にはさまれるスポンジケーキみたいな絵面になりますね！混ぜるな危険！
でも１２月ならショートケーキとターキーのクリスマスセットということで許される気がします！クリスマスは正義！
えー、一切今回の話と関係ない前座でしたが、今回は 前回の記事 で提示した論理パズルの解答とその 参考元 のチェス盤のパズルの解答に共通する性質、完全性について書きます！前回の記事を特に読んでいなくても概要は掴めると思います！
前回の論理パズル
まず、前回の論理パズルの概要がこちら。
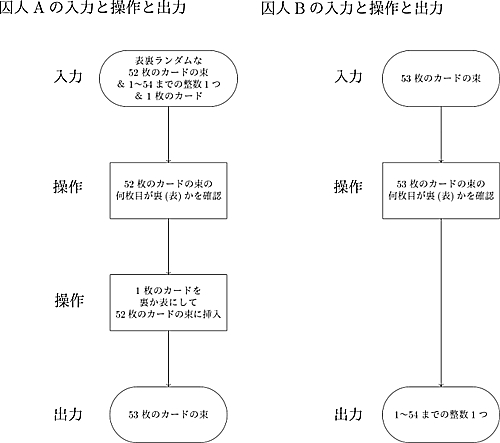
裏表の区別しかない５２枚の同じカードの束を、悪魔が裏表バラバラにシャッフルする。その後、悪魔は囚人Aだけに$1$～$54$までの整数を１つ伝える。
それを聞いた囚人Aは、その５２枚のカードの束に、同じカード１枚を裏か表かにして挿入する。その際、５２枚のカードの束を順番を崩さずに広げて何枚目が裏なのか表なのかを確認してよい。
その後、囚人Bは同様にその５３枚のカードの束の何枚目が裏なのか表なのかだけを確認し、囚人Aに伝えられた整数を当てる。
このゲームを成功させるために、囚人Aと囚人Bはこのゲームのルールを知った上で事前にどのような戦略をとればいいか？
(問題変わってるじゃないか！というツッコミはご容赦あそばせ。)
つまり、囚人Aと囚人Bの入力と操作の一部と出力は以下の通り。
input
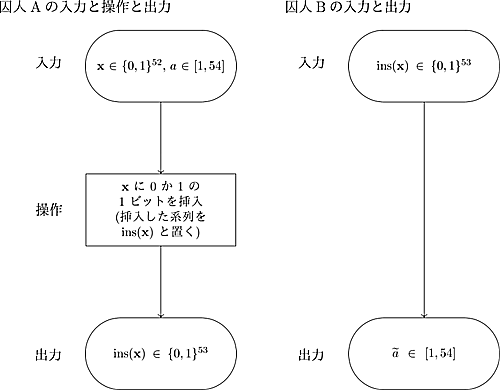
数式で表すとこんな感じ。(区間$[1,54]$は$1$から$54$までの整数の集合を表します。)
input2
$\widetilde{a}=a$となるような囚人Aの操作と囚人Bの操作を具体的に問うているのがこの論理パズルになります。
論理パズル(カード)の解説
この論理パズルの解答を、前回定義したVT符号とその性質を用いて解説していきます。
VT符号の定義とその性質を以下に再掲します。自然数は$1$以上の整数のことだとします。
$n:$自然数, $a:$整数に対して、集合${\text{VT}}_a(n)$を以下で定める。
$${\text{VT}}_a(n) \\
:=\{(x_1,x_2,\cdots, x_n)\in\{0,1\}^n\mid 1x_1+2x_2+\cdots+nx_n\equiv a \pmod {n+1} \} $$
この集合を符号長$n$,パラメータ$a$のVT符号と呼ぶ。
VT符号の元を符号語と呼ぶ。
整数$a$は実際は$1$から$n+1$までの整数のうちの一つ($a\in[1,n+1]$)で代表させても構いません。
$a \equiv a' \pmod {n+1}$であれば${\text{VT}}_a(n)={\text{VT}}_{a'}(n)$であり、
$a \not\equiv a' \pmod {n+1}$であれば${\text{VT}}_a(n)\neq{\text{VT}}_{a'}(n)$である為です。
任意の自然数$n$と任意の整数$a$に対して、
$$\{0,1\}^{n-1}=\bigcup_{{\bf x}\in{\text{VT}_a(n)}} \text{dS}({\bf x}) $$
かつ、相異なる符号語${\bf x},{\bf x'}\in \text{VT}_a(n)$に対して、
$$ \text{dS}({\bf x}) \cap \text{dS}({\bf x'})=\emptyset$$
が成り立つ。ただし、$\text{dS}({\bf x})$はビット列${\bf x}$から一文字削除して得られる系列全体の集合(＝削除球面(deletion sphere))を表す。
$${\text{VT}}_0(4)=\{(x_1,x_2,x_3,x_4)\in\{0,1\}^4\mid 1x_1+2x_2+3x_3+4x_4\equiv 0 \pmod {5} \} \\
=\{0000,0110,1001,1111\} $$
($0000$は$(0,0,0,0)$の略記です。)
$$\{0,1\}^3 \\ =\bigcup_{{\bf x}\in{\text{VT}_0(4)}} \text{dS}({\bf x}) \\ =\text{dS}(0000)\cup\text{dS}(0110)\cup\text{dS}(1001)\cup\text{dS}(1111) \\ =\{000\}\cup\{110,010,011\}\cup\{001,101,100\}\cup\{111\} \\ =(長さ3のビット列全体)$$
上記の完全性の例は前回の「お前、どこ産？」の例と同じものです。
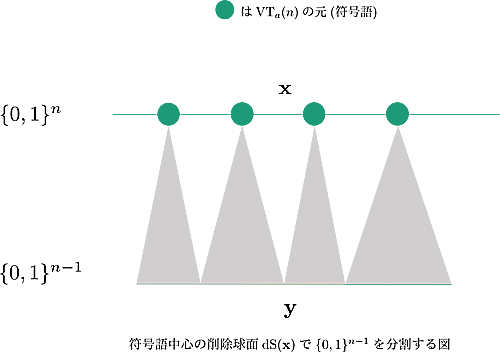
さらに自然数$n$と整数$a$を固定したとき、定理１の様子を図示するとこんな感じ。
perfect1
灰色の三角形(の底辺)が削除球面$\text{dS}({\bf x})$を表しています。符号語${\bf x}$によって要素数が異なるので底辺の長さを変えています。上図のように符号語中心の(単一)削除球面が、符号語の長さより$1$短いビット列全体を直和分割するとき、その(二元)符号を単一削除に対して完全と言います。(符号語の長さは一定とします。)一定の長さのビット列全体を削除球面で充填(sphere packing)、埋め尽くしているイメージです。
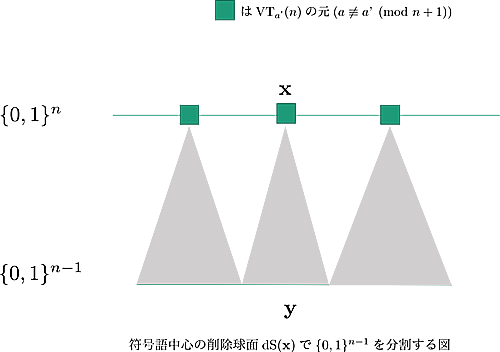
また、VT符号の完全性はパラメータ$a$によらず、$a$を別のパラメータ$a'$に取り替えても成り立ちます。
すなわち整数$a\in[1,n]$の取り方の分だけ、$\text{VT}_{a}(n)$の元を中心とした長さ$n-1$のビット列全体の埋め尽くし方が取れるということになります。
perfect2
(一般に$\text{VT}_a(n)$と$\text{VT}_{a'}(n)$の符号語数(要素数)は同じとは限りません。)
これらの図を見ると前回紹介した定理１の系は納得出来る主張になっていると思います。
任意の自然数$n$と任意の整数$a$と任意のビット列${\bf y}\in \{0,1\}^{n-1}$に対して、${\bf y}$に一文字挿入して得られる符号語${\bf x}\in\text{VT}_a(n)$は一意的に決まり、必ず存在する。
定理１の系がこの論理パズルを解く鍵になります。この定理１の系を用いて、５２枚のカードの束$\rightarrow$１枚のカード(の束)、
$1$～$54$の整数一つを当てる$\rightarrow$$1$～$3$の整数一つを当てる、とした場合の論理パズルの解法を見ていきましょう。
この場合の解法は以下の図の通りです。当てる整数は$1$～$3$です。
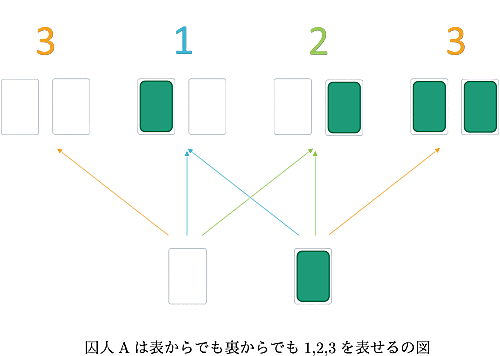figure1
カードの束が１枚しかないので初期状態は表か裏かですが、どちらであっても囚人Aは１枚カードを挿入することで３通りの状態が作れ、上図の数字の割り振り方で囚人Bに$1$～$3$の整数を一つ伝えることが出来ます。
この解法を定理１の系の視点から捉え直します。$a$を$1$～$3$までの整数の一つとしてVT符号$\text{VT}_{a}(2)$を考えると
$$\text{VT}_{1}(2)=\{10\},\qquad \text{dS}(10)=\{0,1\}$$
$$\text{VT}_{2}(2)=\{01\},\qquad \text{dS}(01)=\{0,1\}$$
$$\text{VT}_{3}(2)=\{00,11\},\,\ \text{dS}(00)=\{0\}, \,\ \text{dS}(11)=\{1\}$$
となり、$a=1,2,3$のそれぞれの場合で完全性(削除球面でビット列全体を重なり無く埋め尽くす性質)が成り立っています。
今までは整数$a$を固定して、どんな$y\in\{0,1\}$も一文字挿入して$\text{VT}_{a}(2)$の符号語${\bf x}$に一意的に辿り着けるという見方をしてきました。(下の図で各色が分割を与えているという見方)
しかし、これは$y\in\{0,1\}$を固定して、どんな整数$a\in[1,3]$に対しても、$y\in\{0,1\}$から一文字挿入して$\text{VT}_{a}(2)$の符号語${\bf x}$に一意的に辿り着けるという見方も出来ます。(下の図で各ビット$0,1$から3本の矢印が出ているという見方)
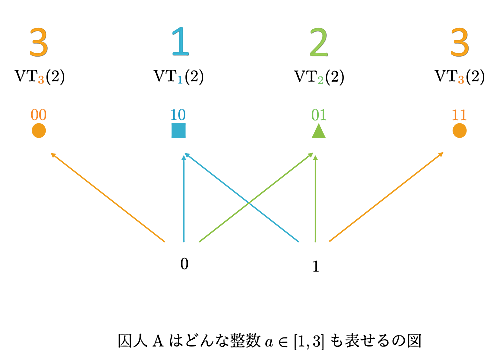figure2
$0$をカードの表、$1$をカードの裏とすれば先ほどの図と完全に対応していますね！(VT符号達で長さ$2$の方のビット列全体を直和分割している点も面白いです！)
結局のところ、定理１の系は整数$a$もビット列${\bf y}$も任意であるため、実際はどちらを先に固定して考えてもいいわけです！
従って、$n=53$としてこの仕組み(完全性)を使えば、カードの束が５２枚からスタートしたとしても必ず囚人Aは囚人Bに好きな整数$a\in[1,53]$を伝えられるわけです！(どうカードを挿入すればいいかは後述。)
囚人Bはカードの表裏を$0,1$に割り当て、長さ53のビット列と自然数列$(1,2,...,53)$との標準内積を$54$で割った余りを計算することで整数$a$を読み解くことが出来ます！(余り$0$は$54$と解釈すればよい。)
これで悪魔に勝てます！VT符号の完全性すごい！
friend
さて、囚人Aのカードの挿入の仕方ですが、定理１の系から与えられた５２枚のカードの束(上から表を$0$、裏を$1$と読むことで長さ$52$のビット列と同一視)に対して、どんな整数$a\in[1,54]$が伝えられたとしても１枚カードを挿入することで、VT符号$\text{VT}_a(53)$の元にすることが必ず出来ます。すなわち、$(1,2,...,53)$との標準内積が$54$余り$a$となるように長さ$53$のビット列を必ず作れます。従って、時間をかけてカードを挿入しては余りが$a$になるかを全通り調べればいいのですが、計算に時間がかかると日が暮れてしまうかもしれません。そこで念のために、以下のアルゴリズムを書き残して解説を終えたいと思います。ちなみにこのアルゴリズムはLevenshteinによって、VT符号が削除･挿入誤り訂正に使えるということと共に、発見されたものです。(実はVT符号は発見当初、削除･挿入とは別の誤りを訂正出来る符号の扱いだった。)
① 与えられた長さ$52$のビット列と$(1,2,...,52)$との標準内積の値を$54$で割った余りをとる。
② ①の値を与えられた整数$a\in[1,54]$から引き、$54$で割った余り($0$～$53$)に直す。(要するに$\mod {54}$をとる。)
③ 与えられた長さ$52$のビット列に含まれる$1$の個数を数える。(裏になっているカードの枚数を数える。)
④ ②の値が③の個数以下である場合、カードは表にして挿入する。挿入位置は挿入する場所より上にある$1$の個数(裏の枚数)が、②の値と一致する場所と決める。(複数の候補がある場合、どこに挿入しても同じ結果になる。)
⑤ ②の値が③の個数より大きい場合、カードは裏にして挿入する。挿入位置は挿入する場所より下にある$0$の個数(表の枚数)が、(②の値)$-$(③の個数)$-1$なる値と一致する場所と決める。(複数の候補がある場合、どこに挿入しても同じ結果になる。)
大変申し訳ありませんが、このアルゴリズムの正しさとVT符号の単一削除誤りに対する完全性の証明は今回は省略いたします！
以上で論理パズル(カード)の解説は終了です！
前回の論理パズルの元になったパズル
前回扱った論理パズルには 参考元 があり、前回のパズルを削除･挿入誤りver.だとするなら、参考元のパズルは反転誤りver.です。(二つの誤りについては 前回の記事 をご参照下さい。)
すなわち、なんと参考元のパズルの方にも反転誤りに対する、ある種の完全性が使われています！そして対応する符号はハミング符号という符号(構造を持った集合)に少し修正を加えた符号になっています。
(個人的に論理パズルは解き方そのものも興味が湧きますが、やはりそのパズルを成り立たせる構造に俄然興味が湧いてしまいます！一般化したいのです！わくわく！)
この節でその視点から参考元のパズルを解説します。
chess
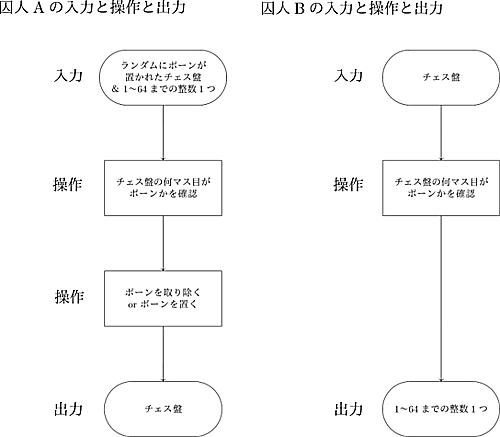
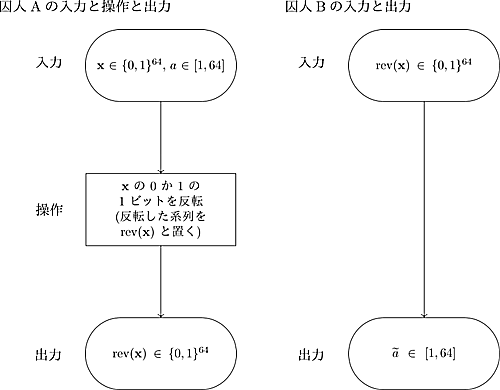
8×8のチェス盤のマスに、悪魔がランダムに同じポーンを好きなだけ(0～64個)置く。その後、悪魔は囚人Aだけに$1$～$64$までの整数を１つ伝える。
それを聞いた囚人Aは、そのチェス盤に対して、ポーンを一つ取り除くか、空いているマスにポーンを一つ置くのどちらか一方を必ず行う。
その後、囚人Bはチェス盤の何マス目にポーンが置いてあるかだけを確認し、囚人Aに伝えられた整数を当てる。
このゲームを成功させるために、囚人Aと囚人Bはこのゲームのルールを知った上で事前にどのような戦略をとればいいか？
このパズルの入力、操作の一部、出力を表したフローチャートはこちら
input3
数式ver.
input4
ここで整数の部分集合である$\{0,1\}$を二元体$\mathbb{F}_2$(**$1+1=0$**が成り立つ集合)に置き換えれば、$1$ビット反転は、ビット列${\bf x} \in\mathbb{F}_2^n$に($i$番目だけ$1$で他が$0$の)単位ベクトル$\boldsymbol{e}_i\in\mathbb{F}_2^n$を、各成分$1+1=0$の規則のもとで足すという代数的な演算で表されます。($n$は自然数, $i\in[1,n]$)
以降、$\{0,1\}$を$\mathbb{F}_2$に置き換えて考えます。$0$は偶数、$1$は奇数を表す記号に変わったと思って下さい。(体として$\mathbb{F}_2\simeq \mathbb{Z}/ 2\mathbb{Z}$であることから、この解釈を用いています。)
ハミング符号について
このパズルを解くのに用いるハミング符号(広義)の定義はこちら。
(前回と同様、符号の構造からパズルの解答に迫ります。)
$m$:自然数, $n:=2^m-1$, ${\bf 0}:=\underbrace{(0,0,\dots,0)}_{mコ}$,
$H$:$\mathbb{F}_2^m$の相異なる非零ベクトル($n$個)全てを列として並べたサイズ$m×n$の行列
に対して、集合$C_{n}\subset \mathbb{F}_2^n$を以下で定める。
$$C_{n}:=\{{\bf x}\in \mathbb{F}_2^n \mid H{\bf x}^{\mathrm{T}}={\bf 0}\}$$
この集合を$m$次のハミング符号と呼ぶ。
混乱の恐れがない限り、ハミング符号の元も符号語と呼ぶ。
要するに行列$H$を左から掛ける線形写像$H(\, \cdot \, )^{\mathrm{T}}:\mathbb{F}_2^n \rightarrow \mathbb{F}_2^m$の核(kernel)です。この写像$H(\, \cdot \, )^{\mathrm{T}}$を改めて$f$と置けば$C=f^{-1}({\bf 0})$と表せます。また、ハミング符号のように線形空間である符号のことを線形符号と呼びます。
ハミング符号は一文字の反転誤りが訂正出来ます。(実は代数的に構成される(反転)誤り訂正符号の中で最も古いものの一つです。)具体例を見ます。
$m:=3$, $n:=2^3-1=7$, ${\bf 0}:=(0,0,0)$,
$$H:=\left(
\begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1\\
0 & 1 & 1 & 0 & 0 & 1 & 1\\
1 & 0 & 1 & 0 & 1 & 0 & 1
\end{array}
\right)$$
($H$は$1$～$7$の二進表記を列ベクトルとして順番に並べた行列だと見なすと分かりやすいと思います。例えば$7$列目はちょうど$(1,1,1)$ですね！)
とすると、$C_{7}$は以下の$\mathbb{F}_2$上の連立方程式の解の集合であり、
$$H{\bf x}^{\text{T}}={\bf 0}\Leftrightarrow \begin{eqnarray}
\begin{cases}
x_4 + x_5 + x_6 + x_7 = 0 & \\
x_2 + x_3 + x_6 + x_7 = 0 & \\
x_1 + x_3 + x_5 + x_7 = 0
\end{cases}
\end{eqnarray}$$
解は$x_3,x_5,x_6,x_7$を決めれば一つに決まる為、$C_{7}\subset\mathbb{F}_2^{7}$は以下の$16$元集合。
$$C_{7}=\{(0,0,0,0,0,0,0),(1,1,0,1,0,0,1),(0,1,0,1,0,1,0),(1,0,0,0,0,1,1),\\
\quad \quad \,\,\ (1,0,0,1,1,0,0),(0,1,0,0,1,0,1),(1,1,0,0,1,1,0),(0,0,0,1,1,1,1), \\
\quad \quad \,\,\ (1,1,1,0,0,0,0),(0,0,1,1,0,0,1),(1,0,1,1,0,1,0),(0,1,1,0,0,1,1), \\
\quad \quad \,\,\ (0,1,1,1,1,0,0),(1,0,1,0,1,0,1),(0,0,1,0,1,1,0),(1,1,1,1,1,1,1) \}$$
ハミング符号といえばこの集合を指すと定義する場合もあります。(狭義の定義)
three
例３の$C_{7}$を引き続き例にとって考えます。ハミング符号$C_7$が$1$ビットの反転誤りを訂正出来るという紹介です。
このとき起こりうる$1$ビットの反転は$1$ビット目から$7$ビット目での反転です。これは単位ベクトル$\boldsymbol{e}_i\in \mathbb{F}_2^7(\, i\in[1,7])$が符号語に足されることだと見なせます。
従って、もし符号語${\bf x}\in C_{7}$に$1$ビット反転が起きたとすると、その状態は${\bf x}+\boldsymbol{e}_i$という形で表されるはずです。$i\in[1,7]$が分かれば、${\bf x}+\boldsymbol{e}_i$の$i$ビット目を反転させることで元の符号語${\bf x}$が分かります。そこで、このベクトルに行列$H$を掛けると、符号語${\bf x}$は$H{\bf x}^{\text{T}}={\bf 0}$を満たすことと行列の積の分配則から、
$$H({\bf x}+\boldsymbol{e}_i)^{\text{T}}=H{\bf x}^{\text{T}}+H\boldsymbol{e}_i^{\text{T}}=H\boldsymbol{e}_i^{\text{T}}$$
が成り立ちます。すなわち、符号語${\bf x}$によらない値になります。また、$\boldsymbol{e}_i$は単位ベクトルなので$H\boldsymbol{e}_i^{\text{T}}=h_i$($h_i$は$H$の$i$列目の列ベクトル)が成り立ちます。この$h_i$は行列$H$の列ベクトルの並び方から二進表記で$i$を表すため、$i$を読み取ることが出来ます。すなわち、元の符号語${\bf x}$が分かります。
例として$C_{7}$の元$(1,1,0,1,0,0,1)$の$3$番目に$1$ビット反転が起こり、$(1,1,{\color{red}1},1,0,0,1)$を受け取ったとします。これに行列$H$を左から掛けることで何番目に誤りが起きたかを診断しましょう。$C_{7}$における行列$H$を再掲します。
$$H:=\left(
\begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1\\
0 & 1 & 1 & 0 & 0 & 1 & 1\\
1 & 0 & 1 & 0 & 1 & 0 & 1
\end{array}
\right)$$
この行列を左から掛けると
$$H(1,1,{\color{red}1},1,0,0,1)^{\text{T}}=(0,1,1)^{\text{T}}$$
となり、二進表記で$011$は$3$ですね！$3$番目に誤りが起きたことが分かったので元の符号語が$(1,1,0,1,0,0,1)$だったと分かります。
ちなみに$1$ビット反転が起きていなければ行列$H$を掛けると${\bf 0}$が返ってくる為、$1$ビット反転が起きなかった場合は何も訂正しなくてよいと判断出来ます。ちなみにこの誤り訂正方法は$2$ビット以上の反転が起きうる場合だと使えません。
例４で、符号語${\bf x}\in C_{7}$から何もしないか、$1$ビット反転して得られる系列全体の集合$\text{B}({\bf x})$(反転球)を考えると、$\text{B}({\bf x})$の要素数は$1+7=8$です。
(中心が入るので球面(sphere)ではなく球(Ball)と呼ぶ方が適切ですが、球面と呼ばれることも多いです。また、一般に反転球や削除球面の概念は適当な距離を用いて定義されます。)
さらに符号語${\bf x},{\bf x'}\in C_{7}$,整数$i,j\in[1,7]$に対して､$${\bf x}+\boldsymbol{e}_i={\bf x'}+\boldsymbol{e}_j\Rightarrow {\bf x}={\bf x'}$$
が成り立ちます。($i=j$ならば明らかで、$i\neq j$の場合は行列$H$を両辺に掛けることで仮定が偽であることが分かるためです。)
このことから符号語${\bf x}$中心の反転球$\text{B}({\bf x})$たちに共通部分は無く、$$\bigcup_{{\bf x}\in{C_{7}}} \text{B}({\bf x})$$の要素数は$8×16=128$であることが分かります。
$\mathbb{F}_2^7$の要素数も$128$であることから、
$$\bigcup_{{\bf x}\in{C_{7}}} \text{B}({\bf x})=\mathbb{F}_2^7$$
であり、反転球たちが長さ$7$のビット列全体を直和分割していることが分かります。$\mathbb{F}_2^7$という空間が反転球$\text{B}({\bf x})$で充填(sphere packing)されているわけです。
こういった性質を持つ符号を完全符号と言います。この性質のことを(単一反転に対する)完全性と呼びます。
一般に以下の性質が成り立つことが分かります。
任意の自然数$m$に対して、
$$\mathbb{F}_2^n=\bigcup_{{\bf x}\in{C_{n}}} \text{B}({\bf x}) $$
かつ、相異なる符号語${\bf x},{\bf x'}\in C_{n}$に対して、
$$ \text{B}({\bf x}) \cap \text{B}({\bf x'})=\emptyset$$
が成り立つ。ただし、$n:=2^m-1$とする。
削除球面とは違い反転球の要素数は一定である為、一般には別の形で(単一)反転誤りに対する完全性が定義されますが、定理２もハミング符号の完全性を表しています。
任意の自然数$m$と任意のビット列${\bf y}\in \mathbb{F}_{2}^{n}\, \backslash\, C_7$に対して、${\bf y}$を一ビット反転して得られる符号語${\bf x}\in C_{n}$は一意的に決まり、必ず存在する。ただし、$n:=2^m-1$とする。
削除のときと同じような定理とその系が導けました！
しかし、このままだと問題点が２つあります。
- 定理１の系にあったパラメータ$a$が無い($a$は悪魔が伝える数字に対応)ため、パズルの解法につながらない。
- 符号の長さは$n:=2^m-1$に固定されているため、$2^6=64$マスのチェス盤に対応しない。
この問題を解決するために、ハミング符号を修正し、このパズルに対応する完全性を考える必要があります。
では、どのような修正をしたらよいでしょうか？
論理パズル(チェス盤)の解説と、ハミング符号の修正
その答えはシンプルで、ハミング符号の符号語の先頭に$0$をつけた系列の集合とハミング符号の符号語の先頭に$1$をつけた系列の集合の和集合をとるだけでOKです。
実際には先頭である必要は無いので一般的には以下のように定式化出来ます。
$m$:自然数, $n:=2^m$, ${\bf 0}:=\underbrace{(0,0,\dots,0)}_{mコ}$,
$H$:$\mathbb{F}_2^m$の相異なるベクトル($n$個)全てを列として並べたサイズ$m×n$の行列
に対して、集合$\text{LC}_{n}\subset \mathbb{F}_2^n$を以下で定める。
$$\text{LC}_{n}:=\{{\bf x}\in \mathbb{F}_2^n \mid H{\bf x}^{\mathrm{T}}={\bf 0}\}$$
この集合を$m$次の伸長ハミング符号と呼ぶ。
混乱の恐れがない限り、伸長ハミング符号の元も符号語と呼ぶ。
(この集合は通常の誤り訂正の能力を失っているので符号と呼ぶべきかは怪しく、伸長ハミング符号はこのブログだけの用語です。)
ハミング符号と異なる点は$H$の列ベクトルに零ベクトルを許していることです。例３の$H$は$0$～$7$の二進表記を列ベクトルとして順番に並べた行列に対応します。
完全性の方もこの符号に合わせたものになります。
任意の自然数$m$に対して、
$$\mathbb{F}_2^n=\bigcup_{{\bf x}\in{\text{LC}_{n}}} \text{S}({\bf x}) $$
かつ、相異なる符号語${\bf x},{\bf x'}\in \text{LC}_{n}$に対して、
$$ \text{S}({\bf x}) \cap \text{S}({\bf x'})=\emptyset$$
が成り立つ。ただし、$n:=2^m$とし、$\text{S}({\bf x})$はビット列${\bf x}$から$1$ビット反転して得られる系列全体の集合を表す。
完全性の気持ちとしては、特定の誤りを考えたとき、起こりうる(受信しうる)系列全体が元の空間と一致してる！です。ハミング符号の完全性における反転球$\text{B}({\bf x})$が反転球面$\text{S}({\bf x})$に置き換わっているため、伸長ハミング符号における完全性は、送信したい符号語${\bf x}$は受信者にそのまま届くことは絶対に無く、必ず$1$ビットの反転が起きるという仮定の下で意味を持つ概念です。(＃どんな状況)この仮定の下であれば、伸長ハミング符号は$1$ビット反転誤り訂正が行えます。
伸長したことにより符号語の長さを$n:=2^m$にすることが出来たため、$64$マスのチェス盤に対応させることが出来ました。
残りはパラメータ$a$ですね！完全性を満たす集合を$a\in [1,2^m]$の分だけ見つけましょう！これは準同型定理からいけそうです！
削除のときと同じく小さな具体例を見ることで一般の場合につなげます！
チェス盤が４マスで、$1$～$4$の整数の一つを当てる場合を考えます。
$0\in \mathbb{F}_2$をポーンが置かれていないマス、$1\in \mathbb{F}_2$をポーンが置いてあるマスに対応させます。さらにチェス盤のマスに番号をふり、チェス盤の状態を$\mathbb{F}_2^4$の元と同一視します。
行列$H$として$0$～$3$の二進表記を列ベクトルとして順番に並べた行列と見なしたものをとると
$$H:=\left(
\begin{array}{cccc}
0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 \\
\end{array}
\right)$$
であり、行列$H$を左から掛ける線形写像$H(\, \cdot \, )^{\mathrm{T}}:\mathbb{F}_2^4 \rightarrow \mathbb{F}_2^2$を改めて$f$と置けば
$$\text{LC}_4=f^{-1}((0,0)^{\text{T}})$$
$$=(H{\bf x}^{\text{T}}=(0,0)^{\text{T}}\text{の解集合})$$
$$=\{(0,0,0,0),(0,1,1,1),(1,0,0,0),(1,1,1,1)\}$$
は線形空間であり、準同型定理から$\mathbb{F}_2^4\, /\, \text{LC}_4\simeq\mathbb{F}_2^2$です。
$\mathbb{F}_2^4\, /\, \text{LC}_4$の元として$\text{LC}_4$の他には
$$f^{-1}((0,1)^{\text{T}})$$
$$=\{(0,1,0,0),(0,0,1,1),(1,1,0,0),(1,0,1,1)\},$$
$$f^{-1}((1,0)^{\text{T}})$$
$$=\{(0,0,1,0),(0,1,0,1),(1,0,1,0),(1,1,0,1)\},$$
$$f^{-1}((1,1)^{\text{T}})$$
$$=\{(0,0,0,1),(0,1,1,0),(1,0,0,1),(1,1,1,0)\}$$
があります。$\mathbb{F}_2^4\, /\, \text{LC}_4\simeq\mathbb{F}_2^2$より$\mathbb{F}_2^4\, /\, \text{LC}_4$の元は以上の４つです。伸長ハミング符号$\text{LC}_4$以外の上記の３つの集合(元)も$\text{LC}_4$と同様に、単一反転誤りに対する完全性が成り立ちます。その状況は見方を変えると、どんな長さ$4$のビット列${\bf y}\in \mathbb{F}_2^4$からでも適当に$1$ビット反転させることで、好きな$f^{-1}({\bf a}^{\text{T}})$の元にすることが出来るということになります。(${\bf a}\in \mathbb{F}_{2}^2$)
それは各$f^{-1}({\bf a}^{\text{T}})$に単位ベクトル$\boldsymbol{e}_i(i\in[1,4])$が含まれていることからも分かります。
イメージとしては以下の図になります。色を固定して頂点を動かしたり、頂点を固定して色を動かしたりすると面白いです。
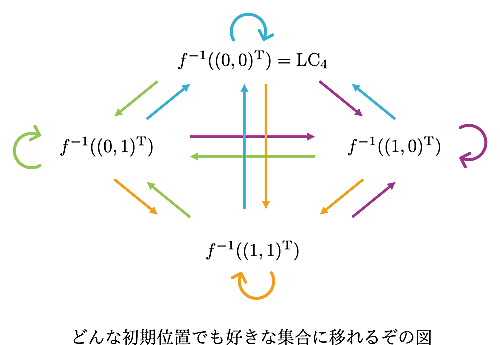colorful
削除の完全性の図と違って、元同士ではなくて集合間の矢印にしています。今回も完全性を与える集合$f^{-1}({\bf a}^{\text{T}})$達の方も$\mathbb{F}_2^4$を直和分割している点が不思議で面白いです。(従って、チェス盤の初期状態は必ずただ一つの$f^{-1}({\bf a}^{\text{T}})$に含まれます。チェス盤の初期状態がどの$f^{-1}({\bf a}^{\text{T}})$に含まれるかは、$H$を左から掛ければ分かります。)
囚人達でこの図を共通認識すれば、囚人Bは受け取ったチェス盤に行列$H$を掛けることで、どんな${\bf a}\in \mathbb{F}_2^2$、もとい$a\in [1,4]$でも読み解くことが出来ますね。(二元体上のベクトルを二進表記と見なして整数と同一視。$(0,0)$は$4$と思えばよい。)
定理$1$の系と対になるように例５でみた内容を定理の形に残します。
任意の自然数$m$と任意のビット列${\bf a}\in \mathbb{F}_2^m$と任意のビット列${\bf y}\in \mathbb{F}_2^{2^m}$に対して、${\bf y}$を$1$ビット反転して得られる元${\bf x}\in f^{-1}({\bf a}^{\text{T}})$は一意的に決まり、必ず存在する。ただし、写像$f$は、$\text{LC}_{n}$の定義に用いる行列$H$を左から掛ける写像$H(\, \cdot \, )^{\mathrm{T}}:\mathbb{F}_2^{2^m} \rightarrow \mathbb{F}_2^m$を表す。
チェス盤のパズルの具体的な解き方は既に解説が書かれた記事があるため、チェス盤のパズルの完全性の視点からの解説は以上にしたいと思います！
(少し触れると、特に例５において$H{\bf x}^{\text{T}}$を計算するということは$$\begin{eqnarray}
\begin{cases}
x_3 + x_4 & \\
x_2 + x_4 &
\end{cases}
\end{eqnarray}$$
の各値、もとい、
$$x_1 \left(
\begin{array}{cccc}
0 \\
0 \\
\end{array}
\right)+
x_2 \left(
\begin{array}{cccc}
0 \\
1 \\
\end{array}
\right)+
x_3 \left(
\begin{array}{cccc}
1 \\
0 \\
\end{array}
\right)+
x_4 \left(
\begin{array}{cccc}
1 \\
1 \\
\end{array}
\right)$$
の値を計算しているということですが、これらの値が
参考元
のサイト様における、$2$進フィルター、もとい、ポーンが置いてある各場所にあたる$2$進数の排他的論理和(XOR)にあたります。)
ちなみにチェス盤のパズルは非負整数$n$に対して、$2^n$マスのチェス盤でないと必勝法がありません。その解説は英語になってしまいますが、純粋な数学コンテンツだけで登録者数が300万人を超えているYoutuber 3Blue1Brownさんの
こちらの動画(The impossible chessboard puzzle)
をご覧下さい。
最後に、このチェス盤のパズルは、2007年秋に
Tournament of the town
という数学オリンピックに準ずる大会において出題されたマジックの問題(Senior A-level 5番)が元になっているそうです！悪魔が言う数字$\rightarrow$観客が言う数字、囚人A$\rightarrow$マジシャンの助手、囚人B$\rightarrow$マジシャンとすれば確かに、マジシャンの助手が一つだけポーンの有る無しを変更したものをマジシャンが一目見て(計算すれば)数字を当てることが出来ますね！(文献[7]参照)
おわりに
全$2$回にわたって、反転と削除それぞれに対する完全性を用いた論理パズルを紹介いたしました。
一文字反転させることと一文字削除することに耐性をもつ仕組みに共通(対応)する性質があることはとても不思議に思います！
ちなみに蛇足になってしまいますが、ある削除誤りに関する完全性に対する研究が、有限コクセター群などの道具を用いて現在もなお進行中です。
例えば$01$もしくは$10$という連続する二文字でビットが異なるものが削除される誤りに関して完全性を満たすものが見つかっています。
５４枚のカードの論理パズルの言葉で言うと、
囚人Aは、表裏もしくは裏表と連なった二枚のカードを束に必ず挿入するというルールでも、囚人Bに$1$～$54$までの整数を一つ伝えることが必ず出来るということです。
このとき囚人Aが、どこに挿入すれば整数を伝えられるかというアルゴリズムの構成が自分の研究だったりします。(このパズルと意外な繋がりがあって自分でもびっくりしています。)
また、およそ２ヶ月前(2020/10/27)のプロシーディング(学会発表用の論文)で面白い結果が出ました。５４枚のカードの論理パズルの言葉で言うと、
- 好きな位置に裏か表でカードを挿入し、もう一枚は一番下に裏か表かでカードを挿入する。
- 一番上に裏表好きな組み合わせでカードを二枚連ねて挿入する(置く)か、または、好きな位置に裏表揃えて、カードを二枚連ねるまたは一枚だけ間隔を空くように挿入する。
- 好きな位置に裏か表でカードを挿入し、もう一枚は一番下に、最初に入れたカードと裏表が揃うように挿入するか、または、好きな位置に裏か表でカードを挿入し、もう一枚は一番上に、最初に入れたカードと裏表が異なるように挿入する。
$\cdots$
といったルールたちの中からどれを選んでゲームを始めても、必ず囚人Bに$1$～$108$までの整数を一つを伝えることが出来る。
という完全性が発見されました。選べるルールの個数は$n$を大きくすれば増えていくため、実質無限個の完全性パズルが手に入ったことになります。
もはや面白いというより恐ろしいです$\cdots$。
明日は Mathlog からの マスログ で、matyuuさんによる 偏角の原理を使って五次方程式を解く です！！五次方程式は(数値的に)解ける！
