上半平面の双曲タイリングを描画する話

　上半平面の双曲タイリングの描画レシピ（簡単なもの）。
双曲タイリング
こんな感じのものを作ってみる。
まず角度を決める。そのうちひとつは簡単のため$\pi/2$とする。それは双曲平面だと直線というのが実軸に垂直なものと実軸に直交する半円であるのだけど、それが1点で交わるときのなす角度。だからこの図だと中央やや下方の半円と真ん中の垂直線だけが交わっている部分に相当する。その他、2つの角度を指定する。それらを$m,n$として、
$$\frac{1}{m}+\frac{1}{n}+\frac{1}{2}<1$$
を満たすようにしないといけない。この描画では$4,5$を選んでいる。そこで、
$$\theta = \frac{\pi}{4},~~~\phi = \frac{\pi}{5}$$
とおく。これらに対し次の量：
$$F(\theta,~\phi)=\frac{\cos \phi + \sqrt{\cos^2\phi - \sin^2\theta}}{\sin^2\theta}$$
を計算し、
$$s=F(\theta,~\phi),~~~a=-s\cos\theta$$
とおく。これらより、反射計算を作る。次の3つ。

1. $x<0$のとき、$x=0$で反射（$x=-x$という操作）
2. $x^2+y^2<1$のとき、円$x^2+y^2=1$で反射（反転）
   $ m = 1/(x^2+y^2)$として$x = mx, ~y=my.$
3. $(x-a)^2 + y^2 > s^2$のとき、円$(x-a)^2 + y^2 = s^2$で反射（反転）
   $n = s^2 / ((x-a)^2 + y^2)$として$x = a + n(x - a), ~y = ny.$

これで描画できる。実際のプログラムはこんな感じ。

作品ページ

      let f = 0;
let a = -1.7;
function setup(){
    createCanvas(800, 400);
}

function draw(){
    let r = 400;
    while(r-- && f < 800 * 400){
        let u = f % 800;
        let v = floor(f / 800);
        let c = 0;
        let p = 36;
        let x = u / 400 - 1;
        let y = 1 - v / 400;
        while(p--){
            if(x < 0){
                x = -x; c++;
            }else if(x * x + y * y < 1){
                let m = 1 / (x * x + y * y);
                x *= m; y *= m; c++;
            }else if((x - a) * (x - a) + y * y > 5.78){
                let n = 5.78 / ((x - a) * (x - a) + y * y);
                x = a + n * (x - a); y *= n; c++;
            }else{
                break;
            }
        }
        stroke(0, (c % 4) * 64, 255);
        circle(u, v, 1);
        f++;
    }
}
    

$s$は$s^2$という形でしか使わないので既に計算してある。
$$\theta = \frac{\pi}{4},~~\phi = \frac{\pi}{5}, ~~F(\theta,~\phi)=2.404185\cdots$$
のようになり、
$$s^2 = F(\theta,~\phi)^2 = 5.7801072\cdots,~~~a = -s\cos\theta = -1.700157\cdots$$
のようになるので近似値も妥当である。隣り合う領域は反射回数のパリティが異なるので、2や4で割った余りで反射回数を加工して色付けに使えばタイリングになる。反射回数をそのまま使ってカラフルに仕上げてもいい。

      colorMode(HSB, 100);
stroke((c % 8) * 12 , 50 + (c % 5) * 10, 100);
    

を使った例：
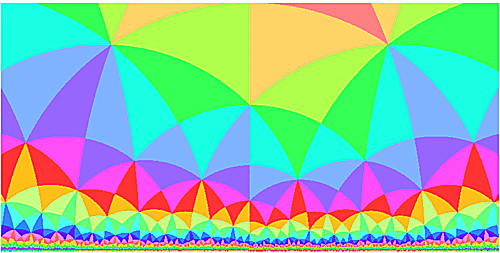カラフル

ただ、普通は$\mathrm{GLSL}$で書いた方がいいと思う。処理も軽くなるし、動きを付けるのもたやすい。

      let myShader;
let vs =
"precision mediump float;" +
"attribute vec3 aPosition;" +
"void main(){" +
"  gl_Position = vec4(aPosition, 1.0);" +
"}";

let fs =
"precision mediump float;" +
"uniform vec2 u_resolution;" +
"const float pi = 3.14159;" +
// 双曲タイリング
"float calc_ref(in vec2 p){" +
"  float theta = pi / 4.0;" +
"  float phi = pi / 5.0;" +
"  float s = (cos(phi) + sqrt(pow(cos(phi), 2.0) - pow(sin(theta), 2.0))) / pow(sin(theta), 2.0);" +
"  float a = -s * cos(theta);" +
"  float c = 0.0;" +
"  const int ITERATION = 64;" +
"  for(int rep = 0; rep < ITERATION; rep++){" +
"    if(p.x < 0.0){" +
"      p.x = -p.x;" +
"      c += 1.0;" +
"    }else if(p.x * p.x + p.y * p.y < 1.0){" +
"      float m = 1.0 / (p.x * p.x + p.y * p.y);" +
"      p.x *= m;" +
"      p.y *= m;" +
"      c += 1.0;" +
"    }else if((p.x - a) * (p.x - a) + p.y * p.y > s * s){" +
"      float n = s * s / ((p.x - a) * (p.x - a) + p.y * p.y);" +
"      p.x = a + n * (p.x - a);" +
"      p.y *= n;" +
"      c += 1.0;" +
"    }else{" +
"      break;" +
"    }" +
"  }" +
"  return c;" +
"}" +
"void main(){" +
"  float u_size = min(u_resolution.x, u_resolution.y);" +
"  vec2 p = (gl_FragCoord.xy * 0.5 - vec2(u_size, 0.0)) / u_size;" +
// なぜか仕様上gl_FragCoordが(0,0)～(1600, 800)になってしまっているので0.5倍して(0,0)～(800,400)にし
// そこから(400,0)を引いて(-400,0)～(400,400)にして400で割って[-1,1]×[0,1]を作り出している。
"  float count = calc_ref(p);" +
"  vec3 col = vec3(0.0, mod(count, 4.0) * 0.25, 1.0);" +
"  gl_FragColor = vec4(col, 1.0);" +
"}";

function setup(){
    createCanvas(800, 400, WEBGL);
  myShader = createShader(vs, fs);
    shader(myShader);
}

function draw(){
    myShader.setUniform("u_resolution", [800, 400]);
    quad(-1, -1, -1, 1, 1, 1, 1, -1);
}
    

GLSLで描いたもの：
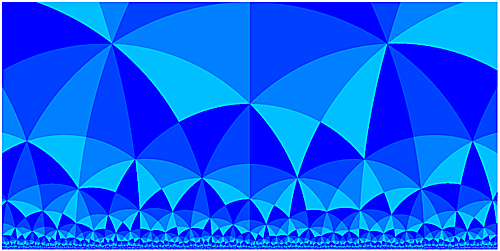双曲GLSL

　応用すると絵柄でやることもできる。
fox1
また、上半平面をポアンカレ円盤に移す写像を使えば、円でタイリングすることもできる。
fox2