コーンの影の問題

${}$

この記事では, 以下のような問題について考えてみます.

マーカーコーン

計算が割と多くなってしまいますが, 面白いと思うので, 最後まで読んでいただけたら幸いです.
${}$

数値設定

まず, 簡単のため, 座標空間で, コーンの下部の円を $\ds\begin{cases}x^2+y^2=9\\[5pt]z=0\end{cases}$, 上部の円を $\ds\begin{cases}x^2+y^2=1\\[5pt]z=1\end{cases}$としましょう. そしてこの2円を下底, 上底とする円錐台の側面を$K$とします.

また, 太陽光は平行光線で, 向きは $\ds\begin{pmatrix}4\\0\\-1\end{pmatrix}$ 方向であるとします.

これは, 上部の円の左端を通った光が下部の円の右端に着くような向きです. もう夕暮れですね.
${}$

$K$を式で表す

$K$を$z$軸に垂直な平面で切ったときの断面が$r$であるとします.$(1\leq r\leq3)$

このような平面は, 円錐の頂点が$z=\frac32$であることから, $z=\frac{3-r}{2}$ですので,

$$\beq K&:&\begin{cases}x^2+y^2=r^2\\[5pt] z=\frac{3-r}2 \end{cases}\sp(1\leq r\leq3)\\[5pt] &\Lra& x^2+y^2=(3-2z)^2\sp(0\leq z\leq1) \eeq$$
と書けます.
${}$

光線$l$を式で表す

上部の円周上の点$(\cos t,\sin t,1)\sp(0\leq t<2π)$を通る光線を$l$とします.

光線の$y$成分は$0$でしたから, $l$は平面$y=\sin t$内の, 傾き$-\frac14$の直線で,

$$ l:\begin{cases}z-1=-\frac14(x-\cos t)\\[5pt] y=\sin t\end{cases} $$
と書けます.
${}$

$K$と$l$の交点を求める

$K$の式に$l$の式を代入して, 交点の$z$座標を求めましょう. $z=1$が解であることは明らかですので, もう一つの解を求めます.

$$\beq && (4+\cos t-4z)^2+\sin^2t=(3-2z)^2\\[5pt] &\Lra& 3z^2-(5+2\cos t)z+2(1+\cos t)=0\\[5pt] &\Lra& (z-1)\left(3z-2(1+\cos t)\right)=0\\ \eeq$$

従って, 交点は $z=\frac23(1+\cos t)$ とわかりました.

$0\leq z\leq 1$ の条件から, $\cos t\leq\frac12$ 即ち $\fracπ3\leq t\leq\frac53π$ である必要があるとわかります.

これは, 上部の円の縁の影が$K$に映るのは$t$がこの範囲の部分の縁だけで, 残りの部分は縁が影を落とすことはないということですね.

$K$の展開図上での影の形を調べる

$K$は円錐ですから切り開くことができるので, その展開図において影がどのような形になるのかを調べます.

と, その前にまずは影の縁$C$をパラメタ表示してみると, $z=\frac23(1+\cos t)$ から
$$ C:\begin{cases} x=\frac13(4-5\cos t)\\[5pt] y=\sin t\\[5pt] z=\frac23(1+\cos t)\end{cases}\sp\big(\fracπ3\leq t\leq\frac53π\big) $$
とわかります.

$C$を$xy$平面に射影すると, 楕円となることがわかりますね.
${}$

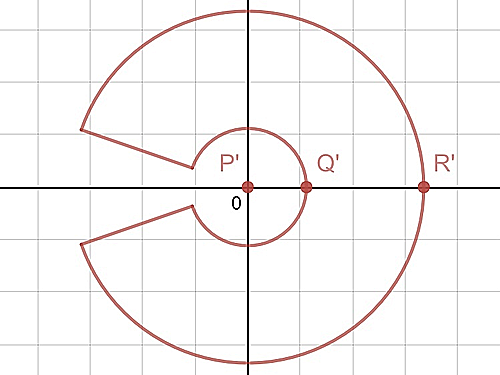
次に, $K$を具体的に切り開いていきます. 円錐$K$(の延長)の頂点を$P(0,0,\frac32)$とし, 他に$K$上の点$Q(1,0,1),\ R(3,0,0)$をとります.

$\ds PQ=\frac{\sqrt5}2,\ PR=\frac32\sqrt5$ なので, $P'(0,0,0),\ Q'(\frac{\sqrt5}2,0,0),\ R'(\frac32\sqrt5,0,0)$ へと移るように切り開く(押しつぶす)ことを考えます.

すると, $K$は扇形のようになり, 中心角は, 母線ぶんの半径ですから, $\ds\frac{2}{\sqrt5}\cdot2π$となります.

K'
${}$

また, $K$上の, $x$座標が$r\cos\t$, $y$座標が$r\sin\t$である点は, このように押しつぶしたことにより, 原点からの距離は$\ds\frac{\sqrt5}{2}$倍, 偏角は$\ds\frac{2}{\sqrt5}$倍になります.

即ち, 極座標のように表せば, 点$\ds\big(\frac{\sqrt5}{2}r,\ \frac{2}{\sqrt5}\t\,\big)$ へと移ることになります.
${}$

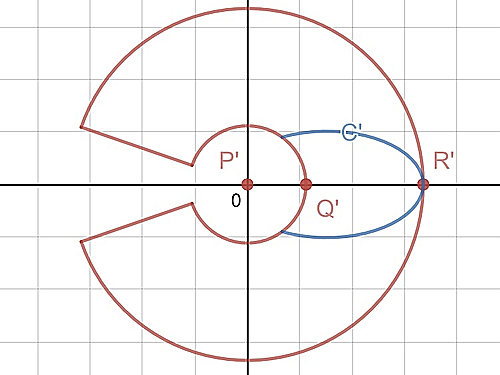
以上より, $C$の$xy$平面への射影$C'$を極座標表示すれば, $C$を$K$と共に切り開いた図形の形もわかるということになりました.

もう一度$C'$をパラメタ表示すると,

$$ C':\begin{cases} x=\frac13(4-5\cos t)\\[5pt] y=\sin t\end{cases}\sp\big(\fracπ3\leq t\leq\frac53π\big) $$

ですから, この楕円の式は
$$ \left(\frac{3x-4}{5}\right)^2+y^2=1\sp\big(\frac12\leq x\leq3\big)$$
となります.

頑張って計算すると, 焦点のひとつは原点であることがわかるので, 楕円の極座標表示の公式(？)(私は覚えていません)から,
$$ r=\frac{3}{5-4\cos\t}\sp\big(-\fracπ3\leq\t\leq\fracπ3\,\big)$$
と, とても綺麗に表せることがわかります.

これを各点に対し$r,\t$を偏倍したものが$C'$ですから, その式は
$$ r=\frac{\sqrt5}{2}\cdot\frac{3}{5-4\cos\frac{\sqrt5}{2}\t}\sp\big(-\frac{2π}{3\sqrt5}\leq\t\leq\frac{2π}{3\sqrt5}\,\big)$$
となることがわかりました！
C'
${}$

ということで, 結局, 楕円の一部だったのですね.

これは, もしかして円錐曲線ということで, 自明なことなのでしょうか？ 平面で切っているわけではないので(上部の穴を通った光線は楕円柱の形になるので), そこまで自明ではないと信じたいですね...
${}$

影の面積を求める

せっかく式を求めたのに, 楕円であることが自明だと言われてしまうと悔しいので, 影の面積$S$を求めてみましょう.

極座標表示で動径の掃く微小面積は$\frac12r^2\,d\t$であることを使います. 中心の扇形の面積を引くのを忘れないように気をつけて,

$$\beq S&=&\int_{-\frac{2π}{3\sqrt5}}^{\frac{2π}{3\sqrt5}}\frac12\Bigg(\frac{\sqrt5}{2}\cdot\frac{3}{5-4\cos\frac{\sqrt5}{2}\t}\Bigg)^2\,d\t-\frac12\Big(\frac{\sqrt5}{2}\Big)^2\cdot\frac{2π}{3\sqrt5}\\[5pt] &=&\frac12\cdot\frac54\cdot9\cdot\frac{2}{\sqrt5}\cdot2\int_0^\fracπ3\frac{d\t}{(5-4\cos\t)^2}-\frac{\sqrt5}{6}π\\[5pt] &=&\frac{9\sqrt5}{2}\int_0^\fracπ3\frac{d\t}{(5-4\cos\t)^2}-\frac{\sqrt5}{6}π \eeq$$
となります.

最後に, $\ds I=\int_0^\fracπ3\frac{d\t}{(5-4\cos\t)^2}$ を計算します.

これは, $\tan\frac\t2$の置換をしてさらにいろいろやると解けるのですが, 長くなるので簡潔に書こうと思います.

$\ds3\tan\frac\t2=\tan\phi$と置換すると, $\ds\phi:0\to\fracπ3$です.

$\ds\cos^2\frac\t2=\frac{9}{9+\tan^2\phi}$, $\ds5-4\cos\t=\frac{9}{\cos^2\phi\,(9+\tan^2\phi)}$ となるので,

$$\beq I&=&\int_0^\fracπ3\frac{1}{(5-4\cos\t)^2}\cdot\frac{2\cos^2\frac\t2}{3}\cdot\frac{d\phi}{\cos^2\phi}\\[5pt] &=&\frac{2}{27}\int_0^\fracπ3\cos^2\phi\,(9+\tan^2\phi)\,d\phi\\[5pt] &=&\frac{2}{27}\int_0^\fracπ3\left(8\cos^2\phi+1\right)\,d\phi\\[5pt] &=&\frac{2}{27}\bigg[2\sin2\phi+5\phi\bigg]_0^\fracπ3\\[5pt] &=&\frac{2}{27}\Big(\sqrt3+\frac53π\Big) \eeq$$
と計算できました.

以上より,
$$\beq S&=&\frac{9\sqrt5}{2}I-\frac{\sqrt5}6π\\[5pt] &=&\frac{\sqrt{15}}{3}+\frac{7\sqrt5}{18}π \eeq$$
と求められました！！！
${}$

おわりに

(たぶん)非自明そうな結果が得られてよかったです. 楕円柱と円錐の交わりが楕円であるということですからね.

また, なかなか解きごたえのある積分もでてきて面白かったです. これ実は, こんな計算をしなくても, 楕円であるということから結構簡単に面積は求まるのですけれど...💦

まあそこは趣味で積分をしたということにさせてください.

ということで, かなり長くなってしまいましたが, ここまで読んで下さった方, 本当にありがとうございました.

${}$

${}$