ルービックキューブ系パズルの数学的な考え方
前提知識 : (特に無し. )
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
定義
以下の定義および問題は, $2\times2\times2$のルービックキューブから各パーツの向きの要素を除いたものを題材としている.
(右手系の) 直交座標空間において, 六つの平面
$$
\begin{align}
x=1,\ x=-1,\ y=1,\ y=-1,\ z=1,\ z=-1
\end{align}
$$をそれぞれ$F,B,R,L,U,D$と名付け, 始めは, これらに囲まれる立方体$C$の頂点
$$
\begin{align}
&(\textcolor{white}{-}1,\textcolor{white}{-}1,\textcolor{white}{-}1),&&(\textcolor{white}{-}1,\textcolor{white}{-}1,-1),\\
&(\textcolor{white}{-}1,-1,\textcolor{white}{-}1),&&(\textcolor{white}{-}1,-1,-1),\\
&(-1,\textcolor{white}{-}1,\textcolor{white}{-}1),&&(-1,\textcolor{white}{-}1,-1),\\
&(-1,-1,\textcolor{white}{-}1),&&(-1,-1,-1)
\end{align}
$$のそれぞれの位置に動点
$$
\begin{align}
a,e,b,f,d,h,c,g
\end{align}
$$を置く. これらの八つの点について, このような配置を「初期配置」と呼ぶ.
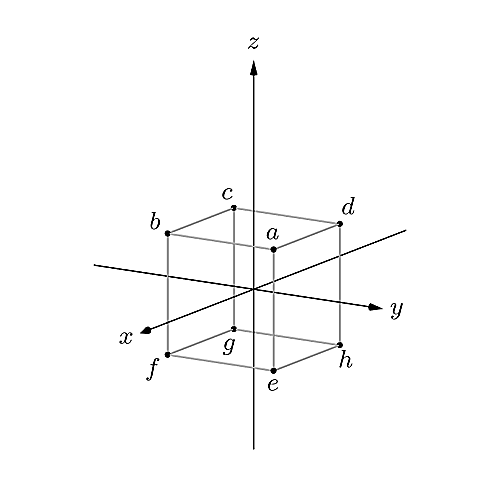 初期配置
初期配置
以下, 八つの点は何れの二つも重ならず, 立方体$C$の頂点の何処かに在るが, 必ずしもその配置が初期配置であるとは限らないとする.
八つの動点のある配置に対する置換$F,B,R,L,U,D$を次の定義によって定める.
定義 : $F$は, 立方体$C$を$F$面の向きから見て$F$面に属する四つの動点を時計回りに$90^\circ$ずつ回す置換である. 他の記号についても同様に考える.
加えて, それぞれの置換の逆操作を$F',B',R',L',U',D'$と記号$'$ (prime) を付して表し, これら十二種の置換を総べて回転と呼ぶ.
八つの動点のある配置が可能であるとは, 幾つかの回転を組みあわせて実行することで, 八つの動点の配置を初期配置に戻すことができることを言う.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
問題
初期配置から回転
$$
\begin{align}
R,U,R',U'
\end{align}
$$をこの順に実行したとき, これによって異なる位置へと移動する動点を全て挙げよ.
初期配置から回転
$$
\begin{align}
R,U,R',U',D,U,R,U',R',D'
\end{align}
$$をこの順に実行したとき, これによって異なる位置へと移動する動点を全て挙げよ.
初期配置から二つの動点$a,b$のみを交換した配置が可能であること, そして, あらゆる動点の配置が可能であることを証明せよ.
$3\times3\times3$のルービックキューブについても, このような考え方を用いることで「可能」であるために必要かつ充分な条件を記述することができ, 実際に任意の「可能」な状態から解くこともできる (興味の有る方は是非挑戦してみてください ! ).
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$