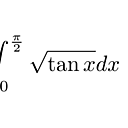【解決済み】上極限についての質問

ここでは、$\{α_n\}_{k}^{∞}$のの上限を$A_k$、$A=\displaystyle\lim_{n\to\infty}$$supα_n$とする。

上極限が有限の時は、任意の$ε>0$に対し、$n_0$があり$n_0\leq n$ならば$α_n< A+ε$が成り立ち、他方$α_n>A-ε$を満たす$α_n$が無限個ある。

$n_0$を$A_{n_0}$<$A+ε$となるようにとれば、$n_0\leq n$のとき$α_n\leq A_{n_0}$で$α_n< A+ε$となる。

$α_n>A-ε$を満たす$α_n$が有限個しかないとすると、$n_0$があり$n_0\leq n$なら $α_n\leq A-ε$となり、$A_{n_0}\leq A-ε$となるがこれは不可能である。

この赤字の部分がなぜそうなるかよく理解できません。初投稿で見づらい部分もあるかと思いますが、どなたかご解答よろしくお願いします。
足りないところや情報があればコメント等で伝えてもらうとありがたいです。

出典:複素解析,L.V.アールフォルス著

投稿日：2020年12月18日

この記事を高評価した人

高評価したユーザはいません

バッジはありません。

1743

アールフォルス博士の『複素解析』をのんびり進めています。難しいことがあったらここで質問させていただきます。ご容赦ください。

コメントはありません。

読み込み中