Birkhoff's variety theorem from Freyd's adjoint functor theorem

143

ISer Advent Calendar 2020 12/16

普遍代数(等式理論)の主要な結果の一つであるBirkhoffの定理って、いかにも一般随伴関手定理使ってくれ〜って顔してませんか？してますね。というわけで一般に知られているものとは異なる、厄介な構成は圏論に投げた証明を考えてみました。自由代数は厄介じゃないです。

本記事では細かい用語の定義はしないのですが、示したい定理であるBirkhoffと使いたい道具である一般随伴関手定理の主張は並べておきます。また空集合もモデルとして認めるものとします。

Birkhoff

言語$\Sigma$を固定し、$\Sigma$代数からなる部分クラス$\mathcal{K}\subset\Sigma\mbox{-Alg}$を考える。このとき次が同値である。

$\mathcal{K}$は部分代数・直積代数・準同型像で閉じている。
ある$\Sigma$上の公理の集合$E$が存在して、$\mathcal{K}=(\Sigma,E)\mbox{-Alg}$となる。

Freyd

圏$\mathcal{B}$をlocally small かつ small complete とし、関手$U:\mathcal{B}\rightarrow\mathcal{A}$を考える。このとき次が同値である。

$U$は左随伴を持つ。
$U$は極限を保ち、また任意のobject $A\in\mathcal{A}$に対し$(A\downarrow U)$は解集合条件を満たす。

Birkhoff

2.ならば1.は簡単なので、1.から2.を示す。

$\Sigma\mbox{-Alg}$を$\Sigma$代数とその準同型のなす圏、$\mathcal{K}$をその充満部分圏だと見なす。このとき$\mathcal{K}$は明らかにlocally smallであり、また直積代数と部分代数で閉じていることからsmall completeかつ集合の圏$\mbox{Set}$への忘却関手が極限を保つ。さらに部分代数で閉じていることから各$(A\downarrow U)$が解集合条件を満たすことも従うので、一般随伴関手定理から左随伴$F:\mbox{Set}\rightarrow\mathcal{K}$が存在。この随伴におけるunitを一つ取り$\eta^F$とする。

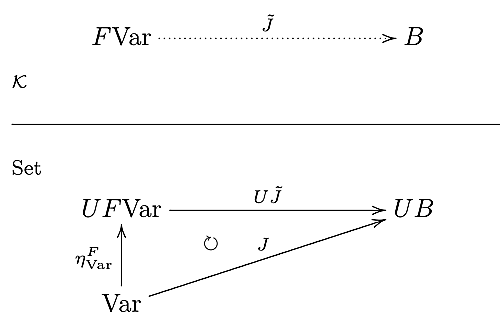
変数の集合を$\mbox{Var}$とすると随伴から、$\mathcal{K}$の任意のobject$B$への任意のvaluation $J:\mbox{Var}\rightarrow UB$は、$\eta^F_{\scriptsize\mbox{Var}}$を通して一意的な準同型$\tilde{J}$で分解できる。

valuation

このとき任意の$\Sigma\mbox{-term}$$t$について$[\![t]\!]_{B,J}=[\![t]\!]_{B,U\tilde{J}\eta^F_{\tiny\mbox{Var}}}=\tilde{J}([\![t]\!]_{F\scriptsize\mbox{Var},\eta^F_{\tiny\mbox{Var}}})$であるので、$\mathcal{K}$の全てのobjectは次で定義される$\Sigma$上の公理の集合$E$を満たす。

$$ E=\{s=t\mid [\![s]\!]_{F{\scriptsize\mbox{Var}},\eta^F_{\tiny\mbox{Var}}}=[\![t]\!]_{F{\scriptsize\mbox{Var}},\eta^F_{\tiny\mbox{Var}}}\} $$

逆に、任意の$(\Sigma,E)$代数は$\mathcal{K}$に属することを示せば、証明は完了である。

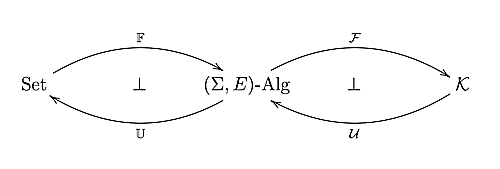
$(\Sigma,E)\mbox{-Alg}$を$(\Sigma,E)$代数全体のなす$\Sigma\mbox{-Alg}$の充満部分圏とする。このとき先ほどと同様に一般随伴関手定理から、忘却関手$\mathcal{U}:\mathcal{K}\rightarrow(\Sigma,E)\mbox{-Alg}$及び$\mathbb{U}:(\Sigma,E)\mbox{-Alg}\rightarrow\mbox{Set}$は共に左随伴を持つ。集合$A$に対し自由$(\Sigma,E)$代数$\mathbb{F}A$はその構成がよく知られていて、集合$A$の元を0変数関数として言語$\Sigma$に加えた$(\Sigma\sqcup A)\mbox{-term}$のうち変数を含まないもの全体の集合の、$E$から誘導される同値関係による剰余からなる。またこのとき$\eta^{\mathbb{F}}_A$は$a\mapsto [a]$である。

adjoint

今、$U=\mathbb{U}\mathcal{U}$より左随伴の一意性から$F\simeq \mathcal{F}\mathbb{F}$が従うので、以下では$F=\mathcal{F}\mathbb{F}$とする。またこのとき$\eta^F=(\mathbb{U}\eta^{\mathcal{F}}_{\mathbb{F}})\eta^{\mathbb{F}}$と取れる。

もし$\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}$が単射でなければ、ある$\Sigma\mbox{-term}$$t$,$u$が存在して$[t]\neq [u]$かつ$\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([t])=\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([u])$が成立するが、このとき

\begin{align} [\![t]\!]_{F(\scriptsize\mbox{Var}),\eta^F_{\tiny\mbox{Var}}} &= [\![t]\!]_{F(\scriptsize\mbox{Var}),\mathbb{U}\eta^{\mathcal{F}}_{\mathbb{F}\tiny\mbox{Var}}\eta^{\mathbb{F}}_{\tiny\mbox{Var}}} \\ &= \eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([\![t]\!]_{\mathbb{F}(\scriptsize\mbox{Var}),\eta^{\mathbb{F}}_{\tiny\mbox{Var}}}) \\ &= \eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([t]) \\ &= \eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([u]) \\ &= \eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([\![u]\!]_{\mathbb{F}(\scriptsize\mbox{Var}),\eta^{\mathbb{F}}_{\tiny\mbox{Var}}}) \\ &= [\![u]\!]_{F(\scriptsize\mbox{Var}),\mathbb{U}\eta^{\mathcal{F}}_{\mathbb{F}\tiny\mbox{Var}}\eta^{\mathbb{F}}_{\tiny\mbox{Var}}} \\ &= [\![u]\!]_{F(\scriptsize\mbox{Var}),\eta^F_{\tiny\mbox{Var}}} \end{align}

が従うので、$E$の定義から$\mathbb{F}\mbox{Var}$が$(\Sigma,E)$代数であることに矛盾する。したがって$\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}$は単射である。同様に任意の無限集合$S$に対し$\eta^{\mathcal{F}}_{\mathbb{F}S}$が単射であることを示す。

任意に$\mathbb{UF}S$の元を2つを固定すれば、それらをそれぞれ$[\![t]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ}$, $[\![u]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ}$と表せるような、$\Sigma\mbox{-term}$$t$,$u$及び写像$J:\mbox{Var}\rightarrow S$が自由代数の構成を考えれば存在する。特に$J$が単射であるようなものが存在するので、そのような$J$とそのretraction$s:S\rightarrow\mbox{Var}$を取る。

unit

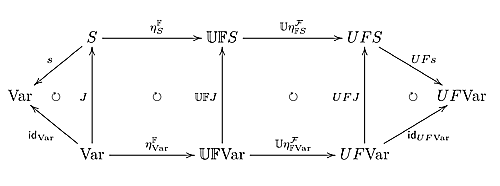
すると任意の$\Sigma\mbox{-term}$$k$に対し、$ \eta^{\mathcal{F}}_{\mathbb{F}S}([\![k]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ})=[\![k]\!]_{FS,\mathbb{U}\eta^{\mathcal{F}}_{\mathbb{F}S}\eta^{\mathbb{F}}_SJ}=[\![k]\!]_{FS,UFJ\mathbb{U}\eta^{\mathcal{F}}_{\mathbb{F}\tiny\mbox{Var}}\eta^{\mathbb{F}}_{\tiny\mbox{Var}}}=FJ\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}([\![k]\!]_{\mathbb{F}{\scriptsize\mbox{Var}},\eta^{\mathbb{F}}_{\tiny\mbox{Var}}})$となる。

今、$UFJ$はsection$UFs$を持つため単射であり、$\eta^{\mathcal{F}}_{\mathbb{F}\scriptsize\mbox{Var}}$は既に見たとおり単射なので、$ \eta^{\mathcal{F}}_{\mathbb{F}S}([\![t]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ})= \eta^{\mathcal{F}}_{\mathbb{F}S}([\![u]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ})$ならば$[\![t]\!]_{\mathbb{F}{\scriptsize\mbox{Var}},\eta^{\mathbb{F}}_{\tiny\mbox{Var}}}=[\![u]\!]_{\mathbb{F}{\scriptsize\mbox{Var}},\eta^{\mathbb{F}}_{\tiny\mbox{Var}}}$である。さらにこのとき$[\![t]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ}=[\![t]\!]_{\mathbb{F}S,\mathbb{UF}J\eta^F_{\tiny\mbox{Var}}}=\mathbb{F}J([\![t]\!]_{\mathbb{F}{\scriptsize\mbox{Var}},\eta^{\mathbb{F}}_{\tiny\mbox{Var}}})=\mathbb{F}J([\![u]\!]_{\mathbb{F}{\scriptsize\mbox{Var}},\eta^{\mathbb{F}}_{\tiny\mbox{Var}}})=[\![u]\!]_{\mathbb{F}S,\mathbb{UF}J\eta^F_{\tiny\mbox{Var}}}=[\![u]\!]_{\mathbb{F}S,\eta^{\mathbb{F}}_SJ}$であるから、$\eta^{\mathcal{F}}_{\mathbb{F}S}$は単射である。

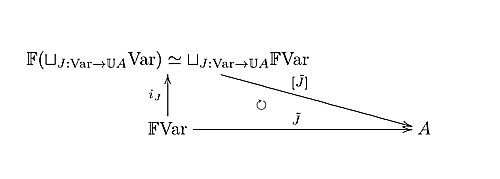
ここまでで任意の無限集合$S$に対し$\eta^{\mathcal{F}}_{\mathbb{F}S}$が単射であることがわかったので、$\mathcal{K}$は部分代数及び準同型像で閉じていることから$\mathbb{F}S$は全て$\mathcal{K}$に含まれる。さらに左随伴は余極限を保つことから、任意の非空$(\Sigma,E)$代数$A$に対し$\mathbb{F}(\sqcup_{J:{\scriptsize\mbox{Var}}\rightarrow\mathbb{U}A}\mbox{Var})$から全射準同型$[\tilde{J}]_{J:{\scriptsize\mbox{Var}}\rightarrow\mathbb{U}A}$が伸び、よって$A$も$\mathcal{K}$に含まれる。