x^3+y^3=(x+y)(x+yω)(x+yω^2)

ただしωは1以外の1の三乗根。奇素数であれば同様に成り立つらしいです。

表題ですが、これは展開すれば簡単です。ちなみに1のn乗根の総和は0になります。

偶数を確かめておきましょう。$ x^{2}+y^{2} $を因数分解しても(x+y)(x-y)にはなりません。また$ x^{4}+y^{4} $も(x+y)(x-y)(x+iy)(x-iy)ではないですね。

一般的に、偶数では成り立たないことがわかります。

今後なんどか記事を掲載しますが、まずは主張したいことを式で書いておきます。

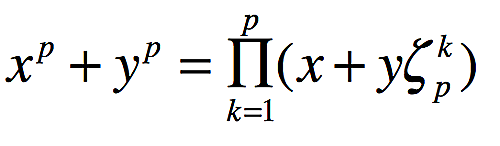x^p+y^p