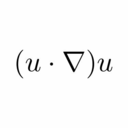平均値の定理の図形的意味とその応用例

図形的意味

よく知られている平均値の定理は以下のようなものである。

この定理の図形的意味を考えよう。まず右辺は、2点$A(a,f(a)),B(b,f(b))$を結ぶ直線の傾きを表している。一方右辺はある点$(c,f(c))$における接線の傾きを表している。これらが等しいということは、直線$AB$の傾きと接線の傾きが等しくなるような接点が存在することを示している。
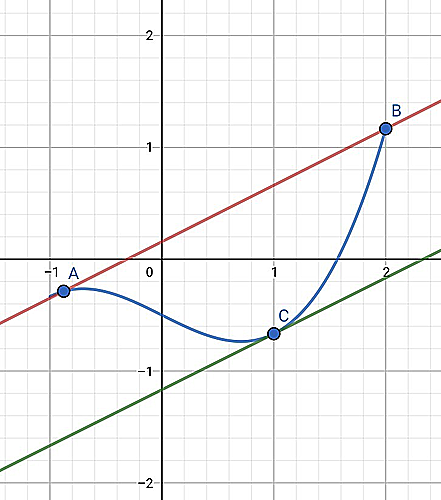図1

今回扱う平均値の定理はこの定理を拡張したものである。これは、Cauchyの平均値の定理と呼ばれている。

Cauchyの平均値の定理において$g(x)=x$としたのがLagrangeの平均値の定理であることは容易にわかる。ではこの定理の図形的意味について考えてみる。議論を簡単にするため$g'(c)\neq0$、$g(b)\neq g(a)$としよう。すると定理2の式は次のように言い換えられる。

これについて考察をしていこう。まず媒介変数$t\in[a,b]$を用いて
$$ x=f(t),\ y=g(t) $$
で描かれる曲線を考える。すると上の式の右辺は、2点$A(f(a),g(a)),B(f(b),g(b))$を結ぶ直線の傾きを表し、左辺はある点$(f(c),g(c))$における接線の傾きを表している。これらが等しいということは、直線$AB$の傾きと接線の傾きが等しくなるような接点が存在することを示している。なお、$g'c)=0$となる場合についても極限を考えれば同様の考察が可能である。

応用例

では、Cauchyの平均値の定理の応用例として、次の問題を解く。

平均値の定理から
$$ \frac{x-\sin x}{x^3}=\frac{1-\cos y}{3y^2} $$
となる$y\in(0,x)$がとれる。再び平均値の定理を用いて、
$$ \frac{1-\cos y}{3y^2}=\frac{\sin z}{6z} $$
となる$z\in(0,y)$がとれる。$x\to+0$のとき$y\to+0$であり$z\to+0$であるので、
$$ \lim_{x\to+0}\frac{x-\sin x}{x^3}=\frac16 $$
である。

最後に

このように平均値の定理は諸々の極限を求める際非常に強力な武器となる。暇があったら証明も書こうと思う。