3
大学数学基礎解説
フィボナッチ数とarctan
94
0
$$\newcommand{BEQ}[0]{\begin{eqnarray}}
\newcommand{C}[0]{\mathbb{C}}
\newcommand{ceil}[1]{\left\lceil#1\right\rceil}
\newcommand{div}[0]{\mathrm{div}}
\newcommand{division}[0]{÷}
\newcommand{EEQ}[0]{\end{eqnarray}}
\newcommand{floor}[1]{ \left\lfloor#1\right\rfloor}
\newcommand{grad}[0]{\mathrm{grad}\ }
\newcommand{hgf}[5]{{}_{#1}F_{#2}\left(\genfrac{}{}{0pt}{}{#3}{#4}\,;\,#5\right)}
\newcommand{IZT}[1]{\mathcal{Z^{-1}}\left[#1\right]}
\newcommand{N}[0]{\mathbb{N}}
\newcommand{Q}[0]{\mathbb{Q}}
\newcommand{R}[0]{\mathbb{R}}
\newcommand{rot}[0]{\mathrm{rot}\ }
\newcommand{Z}[0]{\mathbb{Z}}
\newcommand{ZT}[1]{\mathcal{Z}\left[#1\right]}
$$
フィボナッチ数とarctan
$$ \arctan{\frac{F_{n-3}}{F_{n}}}+\arctan{\frac{F_{n-2}}{F_{n-1}}}=\frac{\pi}{4} $$ただし$F_n$は$n$番目のフィボナッチ数、$n$は$3$以上の整数
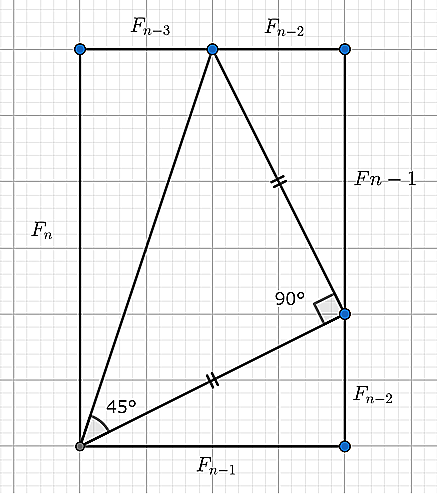 a
a
投稿日:2020年12月25日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
zeta
34
4896
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中