[解答編]領域の面積を4等分する2直線の組に関する補題
こちらは解答編です.
答えを見る前に考えたいという方は
問題編
へ
問題
ユークリッド平面上に有界閉凸領域$D$と直線$l$がある.ただし,$D$の面積は$0$でないとする.
$l$によって$D$が面積の等しい$2$つの領域$D_1,D_2$に分けられているとき,$D_1,D_2$の面積を同時に2等分する直線がただ一つ存在することを示せ.
解答例
存在と一意性をまとめて示します.「同時に$2$等分するときが一度だけある」ではなく,「一本の直線になるときが一度だけある」をゴールに据えてみます.
なお,中間値の定理を適用するときの前提となる連続性を言うために今回は次の定理を用いていますが,これはパズルの本質ではさほどありません.証明は基本的ですので省略します.
$a,b$は$a \leq b$を満たす実数とする.
関数$f:[a,b]\rightarrow \mathbb{R} $が狭義単調減少でありかつ
$$f([a,b])=[f(b),f(a)]$$
であるならば,$f$は連続である.
まず,次の補題を示します.
ユークリッド平面上に有界閉凸領域$K$がある.ただし,$K$の面積は$0$でないとする.
$K$の周上の任意の点$P$をとるとき,$P$を端として$K$の面積を$2$等分する半直線がただ一つ存在する.
領域$K$の面積を$S_K( \gt 0)$とおく.$P$を原点として$K$が領域$x \geq 0$に含まれるような$xy$座標をユークリッド平面に設定できる.
$ \theta \in [-
\frac{\pi}{2} , \frac{\pi}{2}]$に対して半直線$m_ \theta$の方程式を$m_ \theta:y \cos \theta =x \sin \theta$ $(x \geq 0,y\sin \theta \geq 0)$と定める. また,$K$のうち領域$y \cos \theta \geq x \sin \theta$に含まれる部分の面積を$S( \theta)$とする.
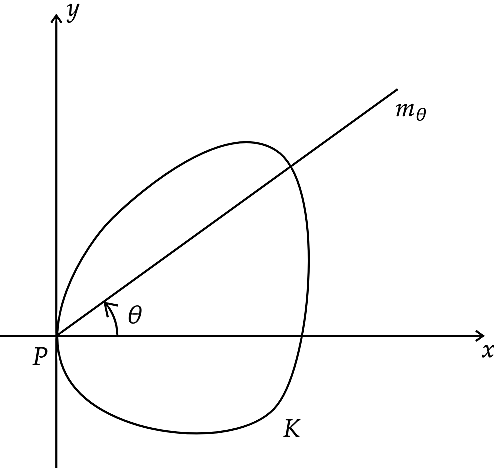
このとき,$K$の周と$m_ \theta$が$P$とは異なる点でも交わるような$\theta$の区間の閉包を$[a,b] \subset [-
\frac{\pi}{2} , \frac{\pi}{2}]$とすると,関数$A:[a,b] \rightarrow \mathbb{R}$は狭義単調減少の連続関数である.
$$S(a)=S_K, S(b)=0$$
であるから,中間値の定理より
$$S( \tilde{ \theta })= \frac{1}{2} S_K $$
をみたす$\tilde{ \theta }\in(-
\frac{\pi}{2} , \frac{\pi}{2})$が唯一つ存在する. $
\blacksquare
$
注) ここでいう閉包は,端点をもつように最小限補ったものと考えてもらって差し支えありません.
では問題の証明に入ります.
$D$の周と$l$は相異なる$2$点で交わり,それらを$A,B$とおけば$D$の周と$l$の共通部分は線分$AB$となる.ある直線$m$が$D_1,D_2$の面積を同時に2等分するならば$m$は$D$の内部,特に線分$AB$と$1$点で交わることに注意する.
$AB=d(\gt 0)$とおく.$x\in [0,d]$に対して$AX=x$となる線分$AB$上の点を$X$とおく.すると補題より$X$を端として$D_1$の面積を$2$等分する半直線$m_1$がただ一つ存在する.同様に$X$を端として$D_2$の面積を$2$等分する半直線$m_2$がただ一つ存在する.
ここで,$0 \lt x \leq d$に対しては半直線$m_1$と半直線$XA$がつくる劣角の大きさを$ \theta_1 (x)$,$x=0$すなわち$X=A$に対しては半直線$m_1$と半直線$XB$がつくる劣角を直線$AB$上の角とみたときの補角の大きさを$ \theta_1 (x)$とすることで関数$ \theta_1:[0,d] \rightarrow \mathbb{R} $を定める.同様にして半直線$m_2$についても関数$ \theta_2:[0,d] \rightarrow \mathbb{R} $を定める.
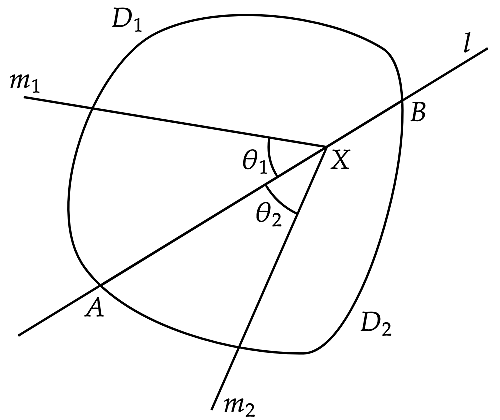
すると$\theta_1, \theta_2
$は定理の仮定をみたすので連続である.よって関数$ \theta
\equiv \theta_1+ \theta_2
$も狭義単調減少の連続関数である.ところで
$$\theta(0) \gt \pi, \theta(d) \lt \pi
$$
であるので中間値の定理から
$$\theta(c)=\pi$$
をみたす,すなわち$m_1 \cup m_2$が直線となるような$c\in(0,d)$が唯一つ存在する. $
\blacksquare
$
注) $\theta_1, \theta_2 $が定理の仮定をみたすことについて,狭義単調減少であることは背理法から,像についての条件は半直線の適当な平行移動を考え中間値の定理を適用することで示せます.
おまけ:$4$回対称性の拡張?
領域の面積を$4$等分する$2$直線の交角に着目します.比較的簡単に次のことがわかります.
ユークリッド平面上に有界閉凸領域$D$がある.
このとき,$D$の面積を$4$等分する$2$直線$l,m$であって直交するものが存在する.
また,こんな予想を考えます.
ユークリッド平面上に有界閉凸領域$D$がある.
このとき,$D$の面積を$4$等分するどんな$2$直線$l,m$も直交するならば,$D$は$4$回対称である.ここで,$D$が$4$回対称であるとは,ある点$P$が存在して$P$を中心とする$ \frac{\pi}{2} $回転について$D$が不変であることをいう.
ちゃんと取り組めていないのですが,解決したorどこかで示されているのを見つけた方がいたら教えてください.
ここで,ユークリッド平面上の有界閉凸領域$D$に対して,$D$の面積を$4$等分する$2$直線のなす(小なる方の)角の大きさの下限を$ \varphi (D)$ $(0 \leq \varphi (D) \leq \frac{\pi}{2})$と定義します.これは最小値にもなっています.すると,上記の予想は「$ \varphi (D)= \frac{\pi}{2} \Longrightarrow$$D$は$4$回対称性をもつ」と言い換えられます.つまり$D$がどれだけ$4$回対称っぽい図形かを判定する目安として$ \varphi (D)$と$\frac{\pi}{2}$の近さを使えるかもしれないということです.尤も,計算は大変そうです.
ここまで読んでいただきありがとうございました.