0
大学数学基礎問題
[問題編]領域の面積を4等分する2直線の組に関する補題
60
0
$$$$
皆さんはじめまして,つむりと申します.早速ですが,挨拶代わりの問題を一つ.
厳密な議論をするなら高校範囲をやや逸脱しますが,それでも証明のアイディアの核心部分は理解できるかと思います.
解答編は
こちら
問題
ユークリッド平面上に有界閉凸領域$D$と直線$l$がある.ただし,$D$の面積は$0$でないとする.
$l$によって$D$が面積の等しい$2$つの領域$D_1,D_2$に分けられているとき,$D_1,D_2$の面積を同時に2等分する直線がただ一つ存在することを示せ.
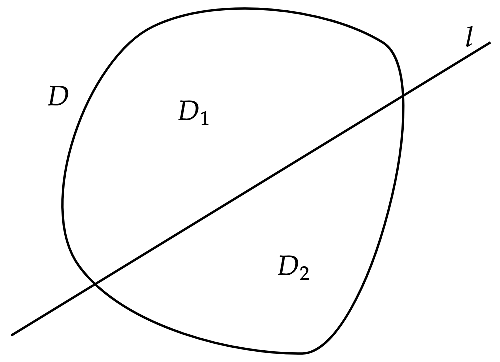 diagram3
diagram3
注) $D$は有界凸であることからJordan可測であり面積が定まります.
ヒント$1$
存在定理の一つ,中間値の定理を使うことを考えます.
ヒント$2$
どうやって関数をつくるかが肝ですが,変数の取り方についてのヒントを.同時に$2$等分する直線が存在すれば必ず$D$の内部の$1$点で$l$と交わります.
投稿日:2020年12月26日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中