複素座標入門4/5 単位円2
お疲れ様です,natuです.今回は単位円2ということで残された五心である内心と傍心について書こうと思います.しかし,この内心・傍心,あまり使いません.大事になるのは内心・傍心の話をする上での注意点です.話が難しいかもしれないのでだるかったらスルーしても構いません.また.内心・傍心だけではあまりにも内容がないようなのでこれを話す前に図形問題の重要な定理である円周角の定理および接弦定理また,回転因子について書こうと思います.それでは,どうぞ.
円周角の定理・接弦定理
円周角の定理を複素座標でも使いたいですね.ということで円周角の定理の主張を複素座標の言葉で言い換えていきます.
4点$A,B,C,D$が同一円周上にある$\displaystyle\Longleftrightarrow\angle BAC+\angle CDB=0,\pi\Longleftrightarrow\arg\frac{a-b}{a-c}+\arg\frac{d-c}{d-b}=\arg\frac{(a-b)(c-d)}{(a-c)(b-d)}=0,\pi$
$\displaystyle\Longleftrightarrow\frac{(a-b)(c-d)}{(a-c)(b-d)}$は実数
これでいいですね!
4点$A,B,C,D$が同一円周上にある$\displaystyle\Longleftrightarrow\frac{(a-b)(c-d)}{(a-c)(b-d)}$は実数
また,これを用いて複素数$z$が三角形$ABC$の外接円周上にあるための条件を考えることができます.
$Z$が三角形$ABC$の外接円周上にある$\displaystyle\Longleftrightarrow\frac{(z-a)(b-c)}{(z-b)(a-c)}$は実数
繰り返しになりますが,この記事で角度というと特に断らない限り符号付き角(有向角)を言います.実際に図を描いて$\angle BAC+\angle CDB=0,\pi$を確かめてみてください.
さて,次は接弦定理です.三角形$ABC$の外接円の点$A$における接線上に点$P$がある場合を考えます.
三角形$ABC$の外接円の点$A$における接線上に点$P$がある
$\Longleftrightarrow\angle PAB+\angle BCA=0,\pi \displaystyle\Longleftrightarrow\arg\frac{a-p}{a-b}+\arg\frac{c-b}{c-a}=\arg\frac{(a-p)(b-c)}{(a-b)(a-c)}=0,\pi$
$\displaystyle\Longleftrightarrow\frac{(a-p)(b-c)}{(a-b)(a-c)}$が実数
三角形$ABC$の外接円の点$A$における接線上に点$P$がある$\displaystyle\Longleftrightarrow\frac{(a-p)(b-c)}{(a-b)(a-c)}$が実数
これらの定理,特に円周角の定理は証明問題のとどめを刺す要員としてよく使われます.
内心・傍心
さあここからが本題,厄介な内心・傍心を扱います.なぜ厄介かというと,これらの点は”角の二等分線”から作図されるからです.角の二等分線は内角,外角を考えると2通りあります.図ではなく式からアプローチする複素座標では角の二等分線が内角のことなのか外角のことなのか判断しづらいのです.厄介ですね…
内心
実は偏角を考えるといい感じです.できるだけ状況を限定したいので$X(1,0)$として
4点$X,A,B,C$はこの順に反時計回りに並んでいるとしましょう.さらに偏角の範囲を限定するために$\arg p=0,0\leq\arg a,\arg b,\arg c\lt2\pi$としましょう.
さて,この状況で弧$AB,BC,CA$(それぞれもう1個の点を含まない方)の中点をそれぞれ$L,M,N$とするとその偏角はそれぞれ
$\displaystyle\arg l=\frac{1}{2}(\arg a+\arg b),\arg m=\frac{1}{2}(\arg b+\arg c),\arg n=\frac{1}{2}(\arg c+\arg a)+\pi$ と表せます.
$\arg n$だけ$\pi$がついてきていやですね.どうすれば点$L,M,N$と点$A,B,C$をうまく3文字で表せるでしょうか.正解は,
$\displaystyle\arg p=\frac{1}{2}\arg a,\arg q=\frac{1}{2}\arg b+\pi,\arg r=\frac{1}{2}\arg c$なる$\omega$上の点$P,Q,R$です.
こうすると$A(p^2),B(q^2),C(r^2),L(-pq),M(-qr),N(-rp)$と表せます.$p,q,r$について対称なのでうれしいですね!さて,これを用いて内心$I$の座標を求めましょう.
直線$BN:z-pq^2r\overline{z}=q^2-pr$ 直線$CL:z-pqr^2\overline{z}=r^2-pq$ この2式から
$z=-qr-rp-pq$が得られます.これが内心$I$の座標です.
 a
a
傍心
内心が求められるなら傍心も求められるでしょう,ということで求めていきます.
$I_A$を求めましょう.外角の二等分線は内角の二等分線と直交することを用います.
直線$BN$に垂直で点$B$を通る直線の方程式は$z+pq^2r\overline{z}=q^2+pr$,
直線$CL$に垂直で点$C$を通る直線の方程式は$z+pqr^2\overline{z}=r^2+pq$
2式より$z$を求めると$z=-qr+rp+pq$となり,これが傍心$I_A$の座標です.
同様にして$I_B(qr-rp+pq),I_C(qr+rp-pq)$も得られます.
"うまく$a,b,c$を取る"とは
ここまでの議論をまとめます.見やすいように$p,q,r$は$a,b,c$に変えておきます.
$\omega$に内接する三角形$ABC$の内心を$I,\angle A,\angle B,\angle C$内の傍心をそれぞれ$I_A,I_B,I_C$とするとき,うまく複素数$a,b,c$を取ると
$A(a^2),B(b^2),C(c^2),I(-bc-ca-ab),I_A(-bc+ca+ab),I_B(bc-ca+ab),I_C(bc+ca-ab)$と表せる.
"うまく$a,b,c$を取る"というのが重要です.また,いつでもこのようにうまく複素数を取ることはできません.たとえば,$\omega$に内接する四角形$ABCD$があるときうまく複素数$a,b,c,d$を取って,三角形$ABC,BCD,CDA,DAB$の内心の座標をそれぞれ$-bc-ca-ab,-cd-db-bc,-da-ac-cd,-ab-bd-da$と表すようなことはできません.
なぜでしょうか?余力があれば考えてみてください.
回転因子
この節では普段問題を解くときに使っている"回転"について"回転因子"(とnatuが勝手に呼んでいる)なる複素数を導入します.簡単な話ですので息抜きだと思ってください.
$\cos\theta+i\sin\theta$を"$\theta$の回転因子"と定義し,$r_\theta$と表す.
当たり前なこととして$|r_\theta|=1,\arg r_\theta=\theta$であり,$A(a)$を原点を中心に$\theta$だけ回転させた点の座標は$r_\theta a$です.また,第2回で話したように,複素数をかけることは"絶対値をかけ,偏角を足す"ことに等しいので次の命題が成り立ちます.
$n$を自然数としたとき
$r_{\theta+\phi}=r_\theta r_\phi, r_{-\theta}=\displaystyle\frac{1}{r_\theta}, r_{n\theta}=r_\theta^n, \overline{r_\theta}=r_{-\theta}$
証明は簡単なので練習問題とします.
第3式は$n$を自然数から整数に拡張することで第2式を内包します.
また,$n$を適切に自然数→整数→有理数→実数と拡張することもできそうですが,ちょっと怖いのでここではあまり踏み込まないことにします.
また,問題を解くときは$\theta$が$60^\circ,54^\circ$など$2\pi$の有理数倍の角度であることが多いです.そのようなときは次のことを忘れないようにしましょう.
$m,n$を$0$でない整数としたとき$\displaystyle\theta=\frac{2m\pi}{n}$に対して
$r_\theta^n=1$,特に$\theta$が$2\pi$の整数倍でないとき$r_\theta^{n-1}+r_\theta^{n-2}+\cdots+r_\theta+1=0$
証明は簡単です.
さて,この"回転因子"を使って任意の点を中心に任意の点を回転移動させましょう.
すなわち点$A(a)$を中心に点$B(b)$を$\theta$だけ回転させた点$C$の座標を考えたいです.
回転の中心を原点に持ってくるためにすべての点を$-a$だけ平行移動して$A^\prime(0),B^\prime(b-a),C^\prime$を考えます.このとき$\theta$の回転因子$r_\theta$を用いて$C^\prime$の座標を表すと$C^\prime(r_\theta(b-a))$となります.これに$a$だけの平行移動を施すと$C$に戻るので$C$の座標は$C(r_\theta(b-a)+a)(=(1-r_\theta)a+r_\theta b)$と表せます.
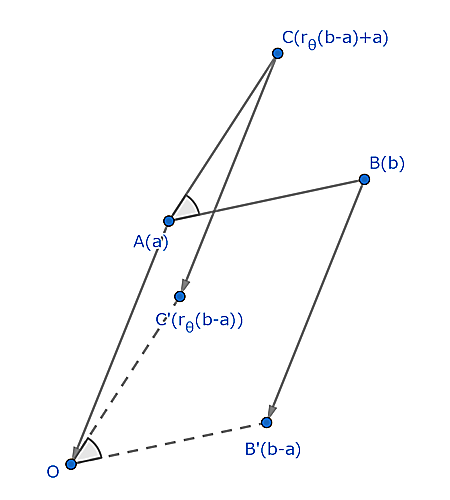 a
a
これでいいですね! ということでまとめます.
$A(a)$を中心に$B(b)$を$\theta$だけ回転移動した点$B^\prime$の座標は$B^\prime((1-r_\theta)a+r_\theta b)$と表される.
繰り返しになりますが回転因子を用いて解くことが望ましい問題はめったにありません.
難角問題をゴリ押すのには役に立つかもしれませんね.
余談ですが,"回転因子"という言葉はnatuの思い付きで命名しました.調べると,類似の概念がすでにあるようで,フーリエ変換(??)に用いられているようです.さっぱりわかりません
練習問題
今回紹介した諸定理を使う問題を探すのは大変で,あまり多くの問題を用意することができませんでした.ただ,円周角の定理だけはよく使います.
level1
$r_\theta,r_\phi$をそれぞれ回転因子,$n$を自然数としたとき次の4式が成り立つことを示せ.
$r_{\theta+\phi}=r_\theta r_\phi, r_{-\theta}=\displaystyle\frac{1}{r_\theta}, r_{n\theta}=r_\theta^n, \overline{r_\theta}=r_{-\theta}$
図のように2つの正五角形と1つの正方形が組み合わさっているとき,3点$A,B,C$は同一直線にあることを示せ.$(natu$の問27$)$
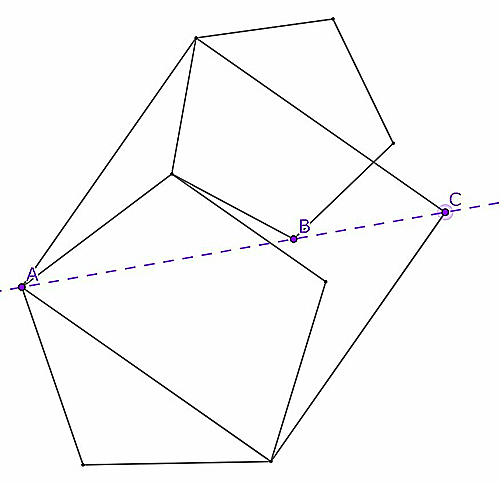 a
a
三角形$ABC$は$AB=AC\neq BC$をみたし,$I$をその内心とする.直線$BI$は辺$AC$と$D$で交わり,$D$を通り直線$AC$に垂直な直線は直線$AI$と$E$で交わる.直線$AC$に関して$I$と対称な点は三角形$BDE$の外接円上にあることを示せ.$($春合宿$2017 4)$
level2
円$\omega$に内接する$\triangle ABC$の内心を$I$,$\angle A$内の傍心を$J$とする.線分$AI$を直径とする円と$\omega$の交点を$P(\neq A)$,$AJ$を直径とする円と$\omega$の交点を$Q(\neq A)$とするとき,$PQ/\!/BC$を示せ.$(peppers 3/30)$
正9角形$A_1A_2\cdots A_9$があり,対角線$A_1A_4,A_3A_5$の交点を$X$,対角線$A_1A_4,A_2A_7$の交点を$Y$とする.$\angle XA_9Y=20^{\circ}$を示せ.$(LAN1729$さんのツイートより$)$
level3
三角形$ABC$の外接円の点$A$を含まない方の弧$BC$上を点$P$が動く.三角形$ABP,ACP$の内心をそれぞれ$I_B,I_C$とするとき三角形$PI_BI_C$の外接円は$P$によらないある定点を通ることを示せ.$(USAJMO 1$改題$)$
次回予告
今回は新しい定理が少ないです.しかし,これで主要な定理は出尽くしました.あとは研鑽あるのみです.ということで次回は実際に問題を解くときのテクニックなどを書きます.問題も難しくなりますよ…
それでは,お疲れさまでした.
