複素座標入門　練習問題まとめ

次の命題を示せ．
(1)任意の複素数$a,b$に対して$\overline{a\pm b}=\overline{a}\pm\overline{b},\overline{ab}=\overline{a}\overline{b}$が成り立つ．
(2)任意の複素数$z$に対して$Re(z)=\displaystyle \frac{1}{2}(z+\overline{z}),Im(z)=\frac{1}{2i}(z-\overline{z}),|z|= \sqrt{z\overline{z}}$,$z$が実数$,\Longleftrightarrow z=\overline{z},z$が純虚数$ \Longleftrightarrow z+\overline{z}=0$．

$4\sqrt{3}+4i$の平方根をすべて求めよ．

平面上に2点$A,B$がある．次の図形の方程式を$a,b$で表せ．
(1)直線$AB$
(2)線分$AB$の垂直二等分線
(3)線分$AB$を直径とする円

次の4つの数のうち複素数$a,b　(|a|,|b|=1)$の値にかかわらず実数となるものをすべて選べ．
$\displaystyle\frac{ab+a+b+1}{a^2+b^2-1},\frac{ab(a+b)}{a^2b^2+a^2b+ab^2+a+b+1},\frac{a^3+b^3}{(a^2+b)(b^2+a)},\frac{(Re(a)+Im(b)i)(Re(b)+Im(a)i)}{Re(ab)+Im(ab)Re(\displaystyle\frac{a^2+b^2}{2ab})i}$

原点$O$,および原点でない異なる点$A,B$に対して三角形$OAB$の重心,外心の座標を求めよ．

平面上に点$O$と点$A$に対して次のような操作を考える．
操作：点$A$を半直線$OA$上の$OA\cdot OA^{\prime}=1$を満たす点$A^{\prime}$に移す．
この操作を図形$X$上のすべての点に対して行ったとき$X$が移る先を$X^{\prime}$とおく．次のことを複素座標を用いて示せ．
(1)$X$が$O$を通らない円のとき,$X^{\prime}$も$O$を通らない円である．
(2)$X$が$O$を通る円のとき,$X^{\prime}$は$O$を通らない直線である．

複素座標を用いてスチュワートの定理を示せ．スチュワートの定理の主張は次のとおりである．
:三角形$ABC$の辺$BC$に点$P$を取ったとき,$AB^2\cdot CP+AC^2\cdot BP=BC(BP\cdot CP+AP^2)$が成り立つ．

直交座標平面上に3点$A(m,n),B(-n,m),C(m-n,m+n)　(m,n)=(0,0)$がある．
複素座標を用いて$\angle BAC=135^{\circ}$を示せ

直線$az+b\overline{z}=c　(a \neq0)$と原点の距離は$b$によらないことを示せ．

(1)絶対値が$r$で偏角が$\theta$である複素数$\alpha$について$Re(\alpha),Im(\alpha)$を求めよ．
　(2)(1)の結果を用いて$|ab|=|a||b|,\arg ab=\arg a+\arg b$が成り立つことを示せ．

三角形$ABC$が正三角形であるとき,$a^3+b^3+c^3=3abc$であることを示せ．

${}_{99} \mathrm{ C }_0+{}_{99} \mathrm{ C }_4+\cdots +{}_{99} \mathrm{ C }_{96}$を計算せよ．

4点$\displaystyle A(a),B(b),A^{\prime}\left(-\frac{1}{\overline{a}}\right),B^{\prime}\left(-\frac{1}{\overline{b}}\right)$は同一直線上に並ぶか同一円周上に並ぶことを示せ

平面上に三角形$ABC$があり,外部に点$P,Q,R,S$を四角形$ABPQ,ACRS$が正方形になるうにとる．点$A$を通り,直線$QS$に垂直な直線は辺$BC$の中点を通ることを示せ．(長岡の教科書Ⅲより)

平行四辺形$ABCD$があり,直線$AB$上に点$E$がある．$A,B,E$はこの順に並んでおり,$BC=BE$をみたす．$A$から直線$CE$へおろした垂線と線分$AE$の垂直二等分線の交点を$X$とするとき,4点$A,B,D,X$は同一円周上にあることを示せ．$(EGMO$一次予選$2020　4)$

円に内接する六角形$ABCDEF$がある．辺$AB$と辺$DE$が平行であり,辺$BC$と辺$EF$が平行であるとき,辺$CD$と辺$FA$も平行であることを示せ．$(JJMO2011　1)$

円に内接する五角形$A_1,A_2,A_3,A_4,A_5$があり,辺$A_3A_4,A_4A_5,A_5A_1,A_1A_2,A_2A_3$の中点をそれぞれ$M_1,M_2,M_3,M_4,M_5$とし,三角形$A_5A_1A_2,A_1A_2A_3,A_2A_3A_4,A_3A_4A_5,A_4A_5A_1$の垂心をそれぞれ$H_1,H_2,H_3,H_4,H_5$とする．このとき,五角形$M_1M_2M_3M_4M_5$と五角形$H_1H_2H_3H_4H_5$は相似であることを示せ．

四角形$ABCD$に点$O$を中心とする円が内接している．対角線$AC,BD$の中点をそれぞれ
$M,N$としたとき,$OM:ON=OA\cdot OC:OB\cdot OD$を示せ．($JMO2011$予選$　11$改題)

鋭角三角形$ABC$において,外心を$O$,垂心を$H$とする．また,$O$を通り直線$BC$に平行な直線と辺$AB,AC$との交点をそれぞれ$P,Q$とし,線分$AH$の中点を$M$とする．このとき,$\angle BMP=\angle CMQ$を示せ．$(JJMO2016　4)$

鋭角三角形$ABC$があり,その外心を$O$とする．3点$A,B,C$から対辺に下ろした垂線の足をそれぞれ$D,E,F$とし,さらに辺$BC$の中点を$M$とする．直線$AD$と直線$EF$の交点を$X$,直線$AO$と直線$BC$の交点を$Y$とし,線分$XY$の中点を$Z$とする．このとき3点$A,Z,M$が同一直線上にあることを示せ．$(JMO2017　3)$

三角形$ABC$の外心を$O$,垂心を$H$とし,直線$AB,BC$上に点$D,E$を,$BC=BE=CD$を満たすようにとる．直線$BE,CD$の交点を$K$とするとき,直線$AK,OH$は直線$BC$上で交わることを示せ．$(peppers　5/7)$

$ABCD$は円$\omega$に内接する四角形であり,$P$は直線$AC$上の点であって,直線$PB$および直線$PD$は$\omega$に接する．$\omega$の点$C$での接線は直線$PD$と点$Q$で交わり,$AD$と点$R$で交わる．直線$AQ$と$\omega$の交点のうち$A$でない方を$E$とする．このとき,3点$B,E,R$は同一直線上にあることを示せ．$(APMO2013　5)$

鋭角三角形$ABC$がある．$A$から$BC$におろした垂線の足を$D$,$BC$の中点を$M$,三角形$ABC$の垂心を$H$とする．三角形$ABC$の外接円$\Gamma$と半直線$MH$の交点を$E$とし,直線$ED$と円$\Gamma$の交点のうち$E$でない方を$F$とする．このとき$\displaystyle\frac{BF}{CF}=\frac{AB}{AC}$が成り立つことを示せ．$(APMO2012　4)$

$n$を自然数としたとき次の4式が成り立つことを示せ．
$r_{\theta+\phi}=r_\theta r_\phi,　r_{-\theta}=\displaystyle\frac{1}{r_\theta},　r_{n\theta}=r_\theta^n,　\overline{r_\theta}=r_{-\theta}$

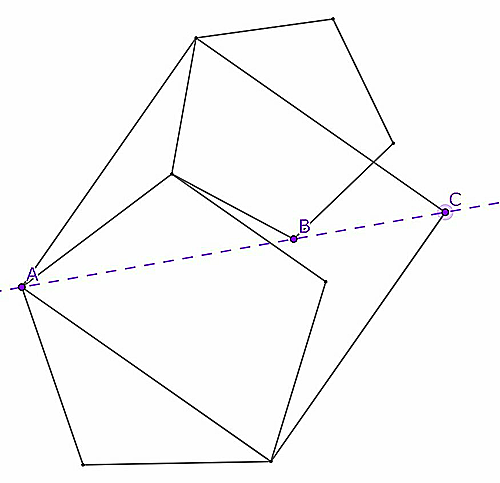
図のように2つの正五角形と1つの正方形が組み合わさっているとき,3点$A,B,C$は同一直線にあることを示せ．$(natu$の問27$)$

a

三角形$ABC$は$AB=AC\neq BC$をみたし,$I$をその内心とする．直線$BI$は辺$AC$と$D$で交わり,$D$を通り直線$AC$に垂直な直線は直線$AI$と$E$で交わる．直線$AC$に関して$I$と対称な点は三角形$BDE$の外接円上にあることを示せ．$($春合宿$2017　4)$

円$\omega$に内接する$\triangle ABC$の内心を$I$,$\angle A$内の傍心を$J$とする．線分$AI$を直径とする円と$\omega$の交点を$P(\neq A)$,$AJ$を直径とする円と$\omega$の交点を$Q(\neq A)$とするとき,$PQ/\!/BC$を示せ．$(peppers　3/30)$

正9角形$A_1A_2\cdots A_9$があり,対角線$A_1A_4,A_3A_5$の交点を$X$,対角線$A_1A_4,A_2A_7$の交点を$Y$とする．$\angle XA_9Y=20^{\circ}$を示せ．$(LAN1729$さんのツイートより$)$

三角形$ABC$の外接円の点$A$を含まない方の弧$BC$上を点$P$が動く．三角形$ABP,ACP$の内心をそれぞれ$I_B,I_C$とするとき三角形$PI_BI_C$の外接円は$P$によらないある定点を通ることを示せ．$(USAJMO　1$改題$)$

三角形$ABC$について,内接円と辺$BC.CA,AB$の接点をそれぞれ$D,E,F$とする．$D$から直線$EF$に下ろした垂線の足を$H$とし,直線$AB$と$CH$の交点を$K$,直線$AC$と$BH$の交点を$L$とする．このとき,$B,C,K,L$は同一直線上にあることを示せ．$(peppers　4/13)$

三角形$ABC$の内部に点$T$を取り,辺$BC,CA,AB$に関して$T$を対称移動したものをそれぞれ$A_1,B_1,C_1$とする．また,三角形$A_1B_1C_1$の外接円を$\Omega$とする．直線$A_1T,B_1T,C_1T$が$\Omega$と再び交わる点をそれぞれ$A_2,B_2,C_2$とする．直線$AA_2,BB_2,CC_2$は$\Omega$上の一点で交わることを示せ．$(shortlist2018　G4)$

鋭角三角形$ABC$の垂心を$H$とし,線分$BC$の中点を$M$とする．$H$を通り直線$AM$に垂直な直線と直線$AM$との交点を$P$とするとき,$AM\cdot PM=BM^2$が成り立つことを示せ．$(JMO2011　1)$

鋭角三角形$ABC$の外心を$O$とする.辺$AB,AC$上(端点を含まない)に点$D,E$をそれぞれ直線$BC$と$DE$が平行とならないようにとり,直線$BC$と$DE$の交点を$F$とおく.$BD$の垂直二等分線と$CE$の垂直二等分線の交点を$K$とおき,直線$KO$と$BC$の交点を$L$とおく.直線$AO$と$DE$の交点を$M$とするとき,4点$F,M,L,O$が同一円周上にあることを示せ.$($春合宿$2019　8)$

$\omega$を内接円に持つ三角形$ABC$がある．$A,B,C$から$BC,CA,AB$へおろした垂線と$\omega$の交点をそれぞれ$P_1$と$P_2$,$P_3$と$P_4$,$P_5$と$P_6$とする．$i=1,2,3$に対して,$P_{2i-1},P_{2i}$での$\omega$の接線の交点を$Q_i$とする．$Q_1,Q_2,Q_3$は同一直線上にあることを示せ．$(peppers　6/2)$

どの辺の長さも相異なる鋭角三角形$ABC$がある．三角形$ABC$の重心$G$と外心$O$を辺$BC,CA,AB$に関して対称移動させた点をそれぞれ$G_1,G_2,G_3,O_1,O_2,O_3$とする．このとき，三角形$G_1G_2C,G_1G_3B,G_2G_3A,O_1O_2C,O_1O_3B,O_2O_3A,ABC$それぞれの外接円は共通の点を通ることを示せ．$(EGMO2017　6)$

三角形$ABC$の内心を$I$,内接円を$\omega$とする．また,辺$BC$の頂点を$M$とする．点$A$を通り直線$BC$に垂直な直線と,点$M$を通り直線$AI$に垂直な直線の交点を$K$とするとき,線分$AK$を直径とする円は$\omega$に接することを示せ．$(JMO2019　4)$

三角形$ABC　(AB\neq AC)$の内心を$I$とし，三角形$ABC$の内接円$\omega$は辺$BC,CA,AB$とそれぞれ点$D,E,F$で接する．点$D$を通り$EF$に垂直な直線は$\omega$と点$R(\neq D)$で交わる．また,直線$AR$は$\omega$と点$P(\neq R)$で交わり,三角形$PCE,PBF$の外接円は点$Q(\neq P)$で交わる．
直線$DI,PQ$は点$A$を通り$AI$に垂直な直線上で交わることを示せ．$(shortlist2019　G7 (IMO2019　6))$

三角形$ABC$の内心を$I$,外心を$O$とし,内接円と辺$BC,CA,AB$の接点をそれぞれ$D,E,F$とする．$O$から直線$DI,EI,FI$に下ろした垂線の足をそれぞれ$P,Q,R$とし,点$P,Q,R$に関して点$A,B,C$と対称な点をそれぞれ$A^{\prime},B^{\prime},C^{\prime}$とする．このとき,三角形$A^{\prime}B^{\prime}C^{\prime}$の外接円は三角形$ABC$の外接円と接することを示せ．$(PPAP1　4)$

不等辺三角形$ABC$の外接円を$\Omega$,内心を$I$とする．直線$AI$は辺$BC$と$D$で交わり,$\Omega$と$M$で再び交わる．線分$DM$を直径とする円は$\Omega$と$K$で再び交わり,直線$MK,BC$は$S$で交わる．また,線分$IS$の中点を$N$とし,三角形$KID$の外接円と三角形$MAN$の外接円は2点$L_1,L_2$で交わっているとする．$\Omega$は線分$IL_1,IL_2$の中点のどちらかを通ることを示せ．$(USAMO2017　3)$

$AB< AC$なる三角形$ABC$において辺$BC$の中点を$M$,三角形$ABC$の外接円の点$A$を含む方の弧の中点を$D$,含む方の弧の中点を$E$とする．三角形$ABC$の内接円と辺$AB$の接点を$F$とし,$AE,BC$の交点を$G$とする．$B$を通り$AB$に垂直な直線と線分$EF$の交点を$N$とする．$BN=EM$のとき,$DF$は$FG$に垂直であることを示せ．$(China Second Round 2018　2)$