複素座標入門　練習問題想定解集

(1)第1式
　　左辺$=\overline{(Re(a)+Im(a)i)\pm(Re(b)+Im(b)i)}=\overline{(Re(a)\pm Re(b))+(Im(a)\pm Im(b))i}$
　　　　$=(Re(a)\pm Re(b))-(Im(a)\pm Im(b))i=(Re(a)-Im(a)i)\pm(Re(b)-Im(b)i)$
　　　　$=$右辺
　　よって左辺$=$右辺．
　　第2式
　　左辺$=\overline{(Re(a)+Im(a)i)(Re(b)+Im(b)i)}=\overline{(Re(a)Re(b)-Im(a)Im(b))+(Re(a)Im(b)+Im(a)Re(b))i}=(Re(a)Re(b)-Im(a)Im(b))-(Re(a)Im(b)+Im(a)Re(b))i$
　　右辺$=(Re(a)-Im(a)i)(Re(b)-Im(b)i)=(Re(a)Re(b)-Im(a)Im(b))-(Re(a)Im(b)+Im(a)Re(b))i$
　　よって左辺$=$右辺．
(2)第1式
　　右辺$\displaystyle=\frac{1}{2}((Re(z)+Im(z)i)+(Re(z)-Im(z)i))=$左辺
　第2式
　　右辺$\displaystyle=\frac{1}{2}((Re(z)+Im(z)i)-(Re(z)-Im(z)i))=$左辺
　第3式
　　三平方の定理より$|z|=\sqrt{Re(z)^2+Im(z)^2}=\sqrt{(Re(z)+Im(z)i}(Re(z)-Im(z)i)=\sqrt{z\overline{z}}$
　第4式
　　第2式より$z$が実数$\Longleftrightarrow Im(z)=0 \Longleftrightarrow z-\overline{z}=0 \Longleftrightarrow z=\overline{z}$
　第5式
　　第1式より$z$が純虚数$\Longleftrightarrow Re(z)=0 \Longleftrightarrow z+\overline{z}=0$
証明終了

$X(x)$が操作によって$X^{\prime}(x^{\prime})$に移るとき,$OX\cdot OX^{\prime}=1$より$x^{\prime}$の絶対値は$\frac{1}{|x|}$であり,$X^{\prime}$が半直線$OX$上にあることから,正の実数$k$を用いて$x^{\prime}=kx$と表される．この式の両辺の絶対値を取って,$\displaystyle |x^{\prime}|=\frac{1}{|x|}$を用いると$\displaystyle k=\frac{1}{|x|^2}$を得るから$\displaystyle x^{\prime}=\frac{1}{\overline{x}}$である．
よって$X(x)$が操作によって$X^{\prime}(\displaystyle\frac{1}{\overline{x}})$に移る．この操作を同じ点に対して2度行うと元の点に戻ることに注意する．
　円は$|z|^2-(\overline{a}z+a\overline{z})+|a|^2=r^2$と表される．
この円は操作によって$z$を$\displaystyle\frac{1}{\overline{z}}$に変えた式すなわち$\displaystyle|\frac{1}{\overline{z}}|^2-(\overline{a}\frac{1}{\overline{z}}+a\overline{(\frac{1}{\overline{z}})})+|a|^2=r^2$に移る．この式の両辺に$|z|^2=z\overline{z}$をかけて整理すると,$(|a|^2-r^2)|z|^2-(\overline{a}z+a\overline{z})+1=0$となり,これは$|a|\neq r$(1)のとき円を表し,$|a|=r$(2)のとき$|z|^2$の項が消え,$z=0$はこの式を満たさないから$O$を通らない直線を表す．証明終了

$P(0),A(a),B(b),C(c)$(ただし,$b,c$は実数で$b>0>c$)と座標を設定する．すると,
左辺$=-|a-b|^2\cdot c+|a-c|^2\cdot b=-(a-b)(\overline{a}-b)c+(a-c)(\overline{a}-c)b=(b-c)(-bc+a\overline{a})=BC(BP\cdot CP+AP^2)=$右辺
証明終了

点$A,B,C$は複素平面では$A(m+ni),B(-n+mi),C((m-n)+(m+n)i)$と表されるから
$\angle BAC=\displaystyle\arg\frac{a-b}{a-c}=\arg\frac{(m+ni)-(-n+mi)}{(m+ni)-((m-n)+(m+n)i)}=\arg\frac{(m+n)+(n-m)i}{n-mi}=\arg(1+i)=45^{\circ}$
証明終了

直線$az+b\overline{z}=c$に垂直な直線は$az-b\overline{z}=p$と表され,これが原点を通るとき$p$である．
2直線$az+b\overline{z}=c,　az-b\overline{z}=0$の交点は$\displaystyle\frac{c}{2a}$であるから,
直線$az+b\overline{z}=c$と原点の距離は$\displaystyle\left|\frac{c}{2a}\right|$と表され,これは$b$によらない．証明終了

(1)のような極形式を考えることで$a=|a|(\cos(\arg a)+i\sin(\arg a)),b=|b|(\cos(\arg b)+i\sin(\arg b))$であるから,
$ab=|a||b|(\cos(\arg a)+i\sin(\arg a))(\cos(\arg b)+i\sin(\arg b))=|a||b|\lbrace (\cos(\arg a)\cos(\arg b)-\sin(\arg a)\sin(\arg b))+i(\cos(\arg a)\sin(\arg b)+\sin(\arg a)\cos(\arg b)) \rbrace$
　$=|a||b|(\cos(\arg a+\arg b)+i\sin(\arg a+\arg b))$
となり,最右辺は絶対値が$|a||b|$で,偏角が$\arg a+\arg b$の複素数の極形式である．
これは$|ab|=|a||b|,\arg ab=\arg a+\arg b$であることを意味する．証明終了

三角形$ABC$が正三角形であるとき$\displaystyle\arg\frac{a-b}{a-c}=60^{\circ},120^{\circ}$かつ$\displaystyle\left|\frac{a-b}{a-c}\right|=1$だから
$\displaystyle\frac{a-b}{a-c}=\frac{1\pm\sqrt{3}i}{2}$である．この式を変形
$\displaystyle\frac{a-b}{a-c}=\frac{1\pm\sqrt{3}i}{2}\Rightarrow a-2b+c=\pm(a-c)\sqrt{3}i\Rightarrow(a-2b+c)^2=-3(a-c)^2$
　　$\Rightarrow a^2+b^2+c^2-ab-bc-ca=0\Rightarrow a^3+b^3+c^3=3abc$
ただし,最後の変形では両辺に$a+b+c$をかけた．証明終了

原点を$O(0)$とする．$\displaystyle\frac{a-0}{\displaystyle -\frac{1}{\overline{a}}-0}=-a\overline{a}$は実数であるから,3点$A,O,A^{\prime}$はこの順に同一直線上にある．よって,3点$A,B,O$が同一直線上にあるとき5点$A,B,O,A^{\prime},B^{\prime}$はこの直線上にある．
,3点$A,B,O$が同一直線上にないとき,点$O$は線分$AA^{\prime},BB^{\prime}$の交点であり,$OA\cdot OA^{\prime}=|a||\displaystyle -\frac{1}{\overline{a}}|=1,同様に$OB\cdot OB^{\prime}=1$である,よって方べきの定理より4点A,B,A^{\prime},B^{\prime}$は同一円周上にある．
証明終了

$A(0),B(b),C(c)$とし,これら3点はこの順に時計回りに並んでいるとする．
このとき点$Q,S$は原点を中心に点$B,C$をそれぞれ$90^{\circ},270^{\circ}$だけ回転移動させたものだから,$Q(ib),S(-ic)$である．よって直線$QS$の方程式は$(\overline{q}-\overline{s})z-(q-s)\overline{z}=\overline{q}s-q\overline{s}$すなわち$(\overline{b}+\overline{c})z+(b+c)\overline{z}=\overline{b}c-b\overline{c}$となり,これに垂直で点$A(0)$を通る直線の方程式は
$(\overline{b}+\overline{c})z-(b+c)\overline{z}=0$となり線分$BC$の中点の座標$\displaystyle\frac{b+c}{2}$はこの方程式を満たす．すなわち点$A$を通り,直線$QS$に垂直な直線は線分$BC$の中点を通る．
証明終了

$B(0)$とし,$A(a),C(b)$($a$は負の実数)とすれば四角形$ABCD$が平行四辺形だから$D(a+b)$
また,$A,B,E$がこの順に並び,$BE=BC=|b|$であることから$E(|b|)$である．
ここで線分$CE$の中点の座標は$\displaystyle\frac{b+|b|}{2}$であり,これと点$B$を結ぶ直線の式は$(\overline{b}+|b|)z-(b+|b|)\overline{z}=0$であり,これは直線$CE$に垂直である．よって$A$から直線$CE$へおろした垂線の方程式は$(\overline{b}+|b|)z-(b+|b|)\overline{z}=p$とおけ,$z=a$を代入して$p=a\overline{b}-ab)$を得るから垂線の方程式は$(\overline{b}+|b|)z-(b+|b|)\overline{z}=a\overline{b}-ab)$である．
また,線分$AE$の垂直二等分線の方程式は$z+\overline{z}=a+|b|$である．
よって$A$から直線$CE$へおろした垂線の方程式と線分$AE$の垂直二等分線の方程式から$z$を求めて$\displaystyle z=\frac{a|b|+\overline{b}|b|+|b|^2+ab}{b+\overline{b}+2|b|}$である．
さて,4点$A,B,D,X$が同一円周上にあることを示すには点$B$を中心とした半径$1$の反転をして,$A,D,X$の移る先が同一直線上にあることを示せばよい．
この反転によって$A(a)$は$\displaystyle A^{\prime}(\frac{1}{a})$に,$D(a+b)$は$\displaystyle D^{\prime}(\frac{1}{a+\overline{b}})$に,$\displaystyle X(\frac{a|b|+\overline{b}|b|+|b|^2+ab}{b+\overline{b}+2|b|})$は$\displaystyle X^{\prime}(\frac{b+\overline{b}+2|b|}{a|b|+{b}|b|+|b|^2+a\overline{b}})$に移る．
$\displaystyle\frac{\displaystyle\frac{1}{a}-x^{\prime}}{\displaystyle\frac{1}{a}-d^{\prime}}=\frac{\displaystyle\frac{1}{a}-\displaystyle\frac{b+\overline{b}+2|b|}{a|b|+{b}|b|+|b|^2+a\overline{b}}}{\displaystyle\frac{1}{a}-\displaystyle\frac{1}{a+\overline{b}}}=\frac{(a+\overline{b})(a\overline{b}+a|b|-\overline{b}|b|-|b|^2)}{\overline{b}(a|b|+ab+\overline{b}|b|+|b|^2)}=\frac{(a+\overline{b})(a-|b|)(\overline{b}+|b|)}{\overline{b}(a+\overline{b})(|b|+b)}=\frac{a-|b|}{|b|}$
よって$\displaystyle\frac{\displaystyle\frac{1}{a}-x^{\prime}}{\displaystyle\frac{1}{a}-d^{\prime}}$は実数であるから3点$A^{\prime},D^{\prime},X^{\prime}$は同一直線上にあるから4点$A,B,D,X$は同一直線上にある．証明終了

円の方程式を$|z|=1$とする．2直線$AB:z+ab\overline{z}=a+b,DE:z+de\overline{z}=d+e$が平行であるから,
$ab=de$であり,同様に$bc=ef$であるからこれら2式より$ab\cdot ef=de\cdot bc$となり$cd=fa$が得られる．
よって2直線$CD:z+cd\overline{z}=c+d,FA:z+fa\overline{z}=f+a$は平行である．証明終了

五角形$A_1A_2A_3A_4A_5$の外接円の方程式を$|z|$とする．
$M_1(\displaystyle\frac{a_3+a_4}{2}),H_1(a_5+a_1+a_2)$より,線分$M_1H_1$を$1:2$に内分する点$X$の座標は$\displaystyle\frac{2m_1+h_1}{3}=\frac{a_1+a_2+a_3+a_4+a_5}{3}$であり,これは$M,H$の添字によらない．
よって$M_1,M_2,M_3,M_4,M_5$を点$X$を中心にして$-2$倍に拡大するとそれぞれ$H_1,H_2,H_3,H_4,H_5$に移る．
これは五角形$M_1M_2M_3M_4M_5$と五角形$H_1H_2H_3H_4H_5$が相似比$1:2$で相似であることを意味する．証明終了

内接する円を$|z|=1$とし,辺$AB,BC,CD,DA$と円の接点をそれぞれ$P,Q,R,S$とする．
このとき,直線$AB,BC,CD,DA$の方程式はそれぞれ
$z+p^2\overline{z}=2p　\cdots①,z+q^2\overline{z}=2q　\cdots②,z+r^2\overline{z}=2r　\cdots③,z+s^2\overline{z}=2s　\cdots④$
となるから,④と①から$a=\displaystyle \frac{2sp}{s+p}$となる．同様に,①と②から$b=\displaystyle \frac{2pq}{p+q}$,
②と③から$c=\displaystyle \frac{2qr}{q+r}$,③と④から$d=\displaystyle \frac{2rs}{r+s}$である．
よって,$m=\displaystyle \frac{a+c}{2}=\displaystyle \frac{sp}{s+p}+\displaystyle \frac{qr}{q+r},n=\displaystyle \frac{b+d}{2}=\displaystyle \frac{pq}{p+q}+\displaystyle \frac{rs}{r+s}$であるから,
$OM^2:ON^2=m\overline{m}:n\overline{n}=(\displaystyle \frac{sp}{s+p}+\displaystyle \frac{qr}{q+r})(\displaystyle \frac{1}{s+p}+\displaystyle \frac{1}{q+r}):(\displaystyle \frac{pq}{p+q}+\displaystyle \frac{rs}{r+s})(\displaystyle \frac{1}{p+q}+\displaystyle \frac{1}{r+s})$
　　　　　　　　　　$=\displaystyle \frac{(pqr+qrs+srp+rpq)(p+q+r+s)}{(s+p)^2(q+r)^2}:\displaystyle \frac{(pqr+qrs+srp+rpq)(p+q+r+s)}{(p+q)^2(r+s)^2}$
　　　　　　$=\left|(p+q)(r+s)\right|^2:\left|(s+p)(q+r)\right|^2$
したがって$OM:ON=|(p+q)(r+s)|:|(s+p)(q+r)|$　また,
$OA\cdot OC:OB\cdot OD=|ac|:|bd|=\left|\displaystyle \frac{4pqrs}{(s+p)(q+r)}\right|:\left|\displaystyle \frac{4pqrs}{(p+q)(r+s)}\right|=|(p+q)(r+s)|:|(s+p)(q+r)|$
である．よって$OM:ON=OA\cdot OC:OB\cdot OD$が示された．

三角形$ABC$の外接円の方程式を$|z|=1$とし,3点$A,B,C$はこの順に時計回りに並んでいるとする．$O$を通り直線$BC$に平行な直線の方程式は$z+bc\overline{z}=0$であり,これと直線$AB:z+ab\overline{z}=a+b$の交点は$\displaystyle z=\frac{ac+bc}{c-a}$だから,$P(\displaystyle\frac{ac+bc}{c-a})$である．
また,$H(a+b+c)$より$M(\displaystyle\frac{2a+b+c}{2})$である．
よって$\displaystyle\angle BMP=\arg\frac{m-b}{m-p}=\arg\frac{\displaystyle\frac{2a+b+c}{2}-b}{\displaystyle\frac{2a+b+c}{2}-\displaystyle\frac{ac+bc}{c-a}}$頑張って計算すると$\displaystyle\angle BMP=\arg\frac{(a-c)(2a-b+c)}{(a+c)(2a+b-c)}$である．$b,c$の対称性より同様に$\displaystyle\angle CMQ=\arg\frac{(a-b)(2a-c+b)}{(a+b)(2a+c-b)}$を得るから,
$\displaystyle\angle BMP+\angle CMQ=\arg\frac{(a-c)(2a-b+c)}{(a+c)(2a+b-c)}+\arg\frac{(a-b)(2a-c+b)}{(a+b)(2a+c-b)}=\arg\frac{(a-b)(a-c)}{(a+b)(a+c)}$となる．
ここで$\displaystyle\overline{\frac{(a-b)(a-c)}{(a+b)(a+c)}}=\frac{\displaystyle(\frac{1}{a}-\frac{1}{b})(\frac{1}{a}-\frac{1}{c})}{\displaystyle(\frac{1}{a}+\frac{1}{b})(\frac{1}{a}+\frac{1}{c})}=\frac{(a-b)(a-c)}{(a+b)(a+c)}$より$\displaystyle\frac{(a-b)(a-c)}{(a+b)(a+c)}$は実数だから
$\angle BMP+\angle CMQ=0^{\circ},180^{\circ}$となり,これと$\angle BMP,\angle CMQ$が鋭角であることから$\angle BMP+\angle CMQ=0^{\circ}$である．よって角度を符号付きでないと考えると$\angle BMP=\angle CMQ$である．証明終了

三角形$ABC$の外接円の方程式を$|z|=1$とする．また,$A(a),B(b),C(c)$とする．
このとき直線$AD$は辺$BC$の垂直で点$A$を通るから方程式は$\displaystyle z-bc\overline{z}=a-\frac{bc}{a}$である,
また,$\displaystyle E(\frac{1}{2}(a+b+c-\frac{ac}{b}))$であり,点$A$における三角形$ABC$の外接円の接線と$EF$は平行だから．
$EF$の方程式は$\displaystyle z+a^2\overline{z}=\frac{1}{2}(a+b+c-\frac{ac}{b})+a^2\cdot \overline{\frac{1}{2}(a+b+c-\frac{ac}{b})}$
整理すると$EF:2bcz+2a^2bc\overline{z}=a^2b+a^2c-ab^2-ac^2+2abc+b^2c+bc^2)$　これと$AD:az-abc\overline{z}=a^2-bc$から点$X$の座標を求めると,$\displaystyle X(\frac{2a^3+a^2b+a^2c-ab^2-ac^2+b^2c+bc^2}{2(a^2+bc)})$である．
また,$AO:z-a^2\overline{z}=0,BC:z+bc\overline{z}=b+c$から,点$Y$の座標を求めると$\displaystyle Y(\frac{a^2(b+c)}{a^2+bc})$である．
よって点$Z$の座標は$\displaystyle Z(\frac{2a^3+3a^2b+3a^2c-ab^2-ac^2+b^2c+bc^2}{4(a^2+bc)})$である．また,$\displaystyle M(\frac{b+c}{2})$である．
ここで$\displaystyle\frac{\displaystyle\frac{b+c}{2}-\frac{2a^3+3a^2b+3a^2c-ab^2-ac^2+b^2c+bc^2}{4(a^2+bc)}}{\displaystyle\frac{b+c}{2}-a}$を頑張って計算すると,$\displaystyle\frac{(a+b)(a+c)}{2(a^2+bc)}$となり,
$\displaystyle\overline{\frac{(a+b)(a+c)}{2(a^2+bc)}}=\cdots=\frac{(a+b)(a+c)}{2(a^2+bc)}$より,$\displaystyle\frac{(a+b)(a+c)}{2(a^2+bc)}$は実数．
よって$\displaystyle A(a),Z(\frac{2a^3+3a^2b+3a^2c-ab^2-ac^2+b^2c+bc^2}{4(a^2+bc)}),M(\frac{b+c}{2})$は同一直線上にある．証明終了

三角形$ABC$の外接円を$\omega$とし,その方程式を$|z|=1$とする．
点$C$から直線$AB$へ下した垂線の足は線分$BD$の中点になるから
$\displaystyle \frac{1}{2}(b+d)=\displaystyle \frac{1}{2}(a+b+c-\displaystyle \frac{ab}{c})$より,$d=a+c-\displaystyle \frac{ab}{c}$である.
よって直線$CD$と$\omega$の交点のうち$C$でないほうを$C^{\prime}$とすると,
$c^{\prime}=\displaystyle \frac{c-d}{c\overline{d}-1}=\displaystyle \frac{c-(a+c-\displaystyle \frac{ab}{c})}{c(\displaystyle \frac{1}{a}+\displaystyle \frac{1}{c}-\displaystyle \frac{c}{ab})-1}=\displaystyle \frac{\displaystyle \frac{ab}{c}-a}{\displaystyle \frac{c}{a}-\displaystyle \frac{c^2}{ab}}=\displaystyle \frac{a^2b}{c^2}$
であるから直線$CD$の方程式を立てるには直線$CC^{\prime}$の方程式を考えればよく,$CD:z+\displaystyle \frac{a^2b}{c}\overline{z}=\displaystyle \frac{a^2b}{c^2}+c$　である．
図形の対称性から直線$BE$の方程式は直線$CD$の方程式において$b,c$を入れ替えたものである．
すなわち,$BE:z+\displaystyle \frac{a^2c}{b}\overline{z}=\displaystyle \frac{a^2c}{b^2}+b$である．この2式から点$K$の座標をもとめる．
方程式$BE\times b^2-$方程式$CD\times c^2$より$(b^2-c^2)z=-a^2(b-c)+(b-c)(b^2+bc+c^2)$
よって$z=\displaystyle\frac{b^2+c^2-a^2+bc}{b+c}$これが点$K$の座標である．
　次に,直線$OH,BC$の交点を$X$とし,その座標を求める．
$H(a+b+c)$より直線$OH$の方程式は$\overline{(a+b+c)}z-(a+b+c)\overline{z}=0$
すなわち$OH:(ab+bc+ca)z-abc(a+b+c)\overline{z}=0$
また,$BC:z+bc\overline{z}=b+c$であるからこれら2式から$z$を求めて
$z=\displaystyle \frac{a^2b+a^2c+ab^2+ac^2+2abc}{a^2+2ab+2ac+bc}$　これが点$X$の座標である
　まとめると,$a,k=\displaystyle \frac{b^2+c^2-a^2+bc}{b+c},x=\displaystyle \frac{a^2b+a^2c+ab^2+ac^2+2abc}{a^2+2ab+2ac+bc}$この3つが同一直線上にあることを示せばよい．
$\displaystyle \frac{a-k}{a-x}=\displaystyle \frac{a-\displaystyle \frac{b^2+c^2-a^2+bc}{b+c}}{a-\displaystyle \frac{a^2b+a^2c+ab^2+ac^2+2abc}{a^2+2ab+2ac+bc}}=\displaystyle \frac{(a^2+2ab+2ac+bc)(a^2+ab+ac-b^2-c^2-abc)}{a(b+c)(a^2+ab+ac-b^2-c^2-abc)}=\displaystyle \frac{a^2+2ab+2ac+bc}{a(b+c)}$ここで
$\overline{(\displaystyle \frac{a-k}{a-x})}=\overline{(\displaystyle \frac{a^2+2ab+2ac+bc}{a(b+c)})}=\displaystyle \frac{\displaystyle \frac{1}{a^2}+\displaystyle \frac{2}{ab}+\displaystyle \frac{2}{ac}+\displaystyle \frac{1}{bc}}{\displaystyle \frac{1}{a}(\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c})}=\displaystyle \frac{a^2+2ab+2ac+bc}{a(b+c)}=\displaystyle \frac{a-k}{a-x}$より$\displaystyle \frac{a-k}{a-x}$は実数である．
よって$a,k,x$は同一直線上に存在するからこれで示された．証明終了

$\omega$の方程式を$|z|=1$とし,$C(1),A(a),D(b)$とおく．
直線$AC,AD$の方程式はそれぞれ$z+a\overline{z}=a+1　\cdots①,z+ab\overline{z}=a+b　\cdots②$
点$C,D$における接線の方程式はそれぞれ$z+\overline{z}=2　\cdots③,z+b^2\overline{z}=2b　\cdots④$
$P$は①と④の交点,$Q$は③と④の交点,$R$は②と③の交点だから点$P,Q,R$の座標を求めると,
$p=\displaystyle\frac{b(ab-2a-b)}{b^2-a},　q=\displaystyle\frac{2b}{b+1},　r=\displaystyle\frac{2ab-a-b}{ab-1}$　である．
点$A,Q$の座標から点$E$の座標を求めて,
$e=\displaystyle\frac{a-q}{a\overline{q}-1}=\displaystyle\frac{a-\displaystyle\frac{2b}{b+1}}{a\overline{(\displaystyle\frac{2b}{b+1})}-1}=$頑張って計算$=\displaystyle\frac{ab+a-2b}{2a-b-1} $
これと点$R$の座標より直線$RE$と$\omega$の交点のうち$E$でない方を$B^{\prime}$とすると$B^{\prime}$の座標は
$b^{\prime}=\displaystyle\frac{e-r}{e\overline{r}-1}=\displaystyle\frac{\displaystyle\frac{ab+a-2b}{2a-b-1}-\displaystyle\frac{2ab-a-b}{ab-1}}{\displaystyle\frac{ab+a-2b}{2a-b-1}\overline{(\displaystyle\frac{2ab-a-b}{ab-1})}-1}=$超頑張って計算$=\displaystyle\frac{ab-2a+b}{-a+2b-1}$
これらの情報から$\angle OB^{\prime}P=90^{\circ}$を示す．
$\angle OB^{\prime}P=\arg \displaystyle\frac{b^{\prime}-p}{b^{\prime}}$より$\displaystyle\frac{b^{\prime}-p}{b^{\prime}}$が純虚数であることを示せばよい．
$\displaystyle\frac{b^{\prime}-p}{b^{\prime}}=\displaystyle\frac{\displaystyle\frac{ab-2a+b}{-a+2b-1}-\displaystyle\frac{b(ab-2a-b)}{b^2-a}}{\displaystyle\frac{ab-2a+b}{-a+2b-1}}=\displaystyle\frac{(a-b)(1-b)}{a-b^2}$より
$\overline{(\displaystyle\frac{b^{\prime}-p}{b^{\prime}})}=\overline{(\displaystyle\frac{(a-b)(1-b)}{a-b^2})}=\displaystyle\frac{(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b})(1-\displaystyle\frac{1}{b})}{\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b^2}}=-\displaystyle\frac{(a-b)(1-b)}{a-b^2}=-\displaystyle\frac{b^{\prime}-p}{b^{\prime}}$だから$\displaystyle\frac{b^{\prime}-p}{b^{\prime}}$は純虚数である．
よって$\angle OB^{\prime}P=90^{\circ}$である．一方で直線$PB$は$\omega$に接するから$\angle OBP=90^{\circ}$である．したがって点$B,B^{\prime}$は一致する．点$B^{\prime}(=B)$が直線$RE$上にあることから
3点$B,E,R$は同一直線上にある．証明終了

$\Gamma$の方程式を$|z|=1$とし,基本計算により$\displaystyle H(a+b+c),M(\frac{b+c}{2})$である．ここで$\Gamma$上の点$A^{\prime}(-a)$を考えると,線分$HA^{\prime}$の中点は$M$に一致する．よって,点$E$は直線$HA^{\prime}$と$\Gamma$の交点のうち$A^{\prime}$でない方といえるので$E$の座標は$\displaystyle\frac{-a-(a+b+c)}{-a(\overline{a+b+c}-1)}$　これを計算して$E(\displaystyle\frac{bc(2a+b+c)}{ab+ac+2bc})$を得る．
これと基本計算より$D(a+b+c-\displaystyle\frac{bc}{a})$
これを用いて点$F$の座標は$\displaystyle\frac{e-d}{e\overline{d}-1}=\frac{\displaystyle\frac{bc(2a+b+c)}{ab+ac+2bc}-(a+b+c-\frac{bc}{a})}{\displaystyle\frac{bc(2a+b+c)}{ab+ac+2bc}\cdot\overline{a+b+c-\frac{bc}{a}}-1}$これを計算して
$\displaystyle F(\frac{a^3b+a^3c+a^2b^2+a^2c^2-ab^2c-abc^2-2b^2c^2}{2a^3+a^2b+a^2c-ab^2-ac^2-b^2c-bc^2})$となる．したがって,
$\displaystyle\frac{BF}{CF}=\left|\frac{f-b}{f-c}\right|=\left|\frac{\displaystyle\frac{a^3b+a^3c+a^2b^2+a^2c^2-ab^2c-abc^2-2b^2c^2}{2a^3+a^2b+a^2c-ab^2-ac^2-b^2c-bc^2}-b}{\displaystyle\frac{a^3b+a^3c+a^2b^2+a^2c^2-ab^2c-abc^2-2b^2c^2}{2a^3+a^2b+a^2c-ab^2-ac^2-b^2c-bc^2}-c}\right|=\left|\frac{(c-b)(a-b)(a^2+ac+bc)}{(b-c)(a-c)(a^2+ac+bc)}\right|=\frac{AB}{AC}\left|\frac{a^2+ac+bc}{a^2+ab+bc}\right|$
また,$\displaystyle\frac{a^2+ac+bc}{a^2+ab+bc}\cdot\overline{\frac{a^2+ac+bc}{a^2+ab+bc}}=\frac{a^2+ac+bc}{a^2+ab+bc}\cdot\frac{a^2+ab+bc}{a^2+ac+bc}=1$より$\displaystyle\left|\frac{a^2+ac+bc}{a^2+ab+bc}\right|=1$である．
よって$\displaystyle\frac{BF}{CF}=\frac{AB}{AC}$が示された．証明終了

第1式について
左辺$=\cos(\theta+\phi)+i\sin(\theta+\phi)=\cos\theta\cos\phi-\sin\theta\sin\phi+i\sin\theta\cos\phi+i\cos\theta\sin\phi=(\cos\theta+i\sin\theta)(\cos\phi+i\sin\phi)=$右辺
第2式について
左辺$\displaystyle=\cos(-\theta)+i\sin(-\theta)=\cos\theta-i\sin\theta=\frac{(\cos\theta+i\sin\theta)(\cos\theta-i\sin\theta)}{\cos\theta+i\sin\theta}=\frac{1}{\cos\theta+i\sin\theta}=$右辺
第3式について
(i)$n=1$のときは明らかに成立
(ii)$n=k$のとき成立すると仮定すると第1式において$\phi=k\theta$として,先ほどの仮定を用いると,
　$r_{(k+1)\theta}=r_\theta r_{k\theta}=r_\theta\cdot r_\theta^k=r_\theta^{k+1}$より$n=k+1$のときも成立する．
(i),(ii)より数学的帰納法から示された．
第4式について
$|r_\theta|=1$と第2式を用いて
左辺$=\displaystyle\frac{1}{r_\theta}=r_{-\theta}=$右辺

以上より4式とも示された．

図のように点$X,Y,Z,W$を取る．$A(0),X(1)$とし,$-108^\circ$の回転因子を$a$とする．また,$90^\circ$の回転因子は虚数単位$i$であることに注意する．
$Y$は$X$を中心に$A$を$-108^\circ$回転したものだから$Y$の座標は$(1-a)\cdot 1+a\cdot 0=1-a$である．
したがって$W(i(1-a))$であり,$c=y+w=(1+i)(1-a)$も従う．また,$\displaystyle Z(\frac{1}{a})$であり,これと$W(i(1-a))$より
$\displaystyle b=(1-a)\frac{1}{a}+a\cdot i(1-a)=(ai+\frac{1}{a})(1-a)$である．
$A,B,C$が同一直線上にあることを示すためには$\displaystyle\frac{b}{c}$が実数であること示せばよく,
$\displaystyle\frac{b}{c}=\frac{\displaystyle ai+\frac{1}{a}}{1+i}=\frac{(\displaystyle ai+\frac{1}{a})(1-i)}{2}=\frac{1}{2}(a(1+i)+\frac{1}{a}(1-i))=\frac{1}{2}(a(1+i)+\overline{a(1+i)})=Re(a(1+i))$
より,確かに$\displaystyle\frac{b}{c}$は実数である．証明終了
a

$\omega:|z|=1$とするとうまく複素数$a,b,c$(いずれも絶対値は$1$)を取って$A(a^2),B(b^2),C(c^2),I(-bc-ab-ac),J(-bc+ab+ac)$と座標設定ができる．$P(p)$は$\angle API=90^{\circ}$より$\displaystyle\frac{p-a^2}{p+bc+ab+ac}$は純虚数．また$|p|=1$より$\displaystyle\overline{p}=\frac{1}{p}$である．
$\displaystyle\frac{p+a^2}{p+bc+ab+ac}$は純虚数だから$\displaystyle-\frac{p-a^2}{p+bc+ab+ac}=\displaystyle\overline{\frac{p-a^2}{p+bc+ab+ac}}=\displaystyle\frac{\displaystyle\frac{1}{p}-\frac{1}{a^2}}{\displaystyle\frac{1}{p}+\frac{1}{bc}+\frac{1}{ab}+\frac{1}{ac}}=\displaystyle-\frac{bc(p-a^2)}{(a^2+ab+ac)p+a^2bc}$となり,この式と$p\neq a^2$より$p=\displaystyle-bc\cdot\frac{a^2-ab-ac-bc}{a^2+ab+ac-bc}$が得られる．同様に$q$を求めるが$I$の座標の$a$を$-a$にすると$J$になるから$p$の座標の$a$を$-a$にすればよく,$q=\displaystyle-bc\cdot\frac{a^2+ab+ac-bc}{a^2-ab-ac-bc}$となる．よって
$\displaystyle\frac{p-q}{b^2-c^2}=\frac{\displaystyle-bc\cdot\frac{a^2-ab-ac-bc}{a^2+ab+ac-bc}+bc\cdot\frac{a^2+ab+ac-bc}{a^2-ab-ac-bc}}{b^2-c^2}=-\frac{bc}{b^2-c^2}\cdot\frac{(a^2-ab-ac-bc)^2-(a^2+ab+ac-bc)^2}{(a^2-ab-ac-bc)(a^2+ab+ac-bc)}=\frac{4abc(a^2-bc)}{(b-c)(a^2-ab-ac-bc)(a^2+ab+ac-bc)}$となり,
$\displaystyle\overline{\frac{4abc(a^2-bc)}{(b-c)(a^2-ab-ac-bc)(a^2+ab+ac-bc)}}=\cdots=\frac{4abc(a^2-bc)}{(b-c)(a^2-ab-ac-bc)(a^2+ab+ac-bc)}$よりこれは実数．$\displaystyle\frac{p-q}{b^2-c^2}$は実数である．よって$PQ$と$BC$は平行．証明終了

$|a|=1$となる実部,虚部ともに正である複素数$a$を用いて$\displaystyle A(1),B(\frac{1}{a^2}),C(a^2)$と表したとき$a$に対応する点と$B$を結ぶ直線は$\angle ABC$を二等分し方程式は$\displaystyle z+\frac{1}{a}\overline{z}=a+\frac{1}{a^2}$,これと$\angle BAC$の二等分線すなわち実軸$:z=\overline{z}$の交点が$I$だから2式から$I$の座標は$\displaystyle \frac{a^2-a+1}{a}$(以下これを$j$とおく)となる．
2直線$\displaystyle BI:z+\frac{1}{a}\overline{z}=a+\frac{1}{a^2},AC:z+a^2\overline{z}=a^2+1$から$D$の座標が求まり,計算すると$\displaystyle D(\frac{a^3-a^2+1}{a^2+a+1})$である．また,これを通り,直線$\displaystyle AC:z+a^2\overline{z}=a^2+1$に垂直な直線の方程式は$\displaystyle z-a^2\overline{z}=\frac{a^3-a^2+1}{a^2+a+1}-a^2\cdot\overline{\frac{a^3-a^2+1}{a^2+a+1}}=\frac{-a^4+a^3-a+1}{a^2+a+1}$となり,これと$AI:z=\overline{z}$から$E$の座標が求まり,計算すると$\displaystyle E(\frac{a^2-a+1}{a^2+a+1})$である．
$\displaystyle I(\frac{a^2-a+1}{a})$を通り,直線$\displaystyle AC:z+a^2\overline{z}=a^2+1$に垂直な直線の方程式は$\displaystyle z-a^2\overline{z}=\frac{a^2-a+1}{a}-a^2\cdot\overline{\frac{a^2-a+1}{a}}=\frac{-a^4+a^3-a+1}{a}$これと$\displaystyle AC:z+a^2\overline{z}=a^2+1$の交点を$H$とし,座標を2式から求めると$H(\displaystyle\frac{-a^4+2a^3+1}{2a})$である．
直線$AC$に関して$I$と対称な点を$I^{\prime}$とおくと線分$II^{\prime}$の中点が点$H$に一致するから$j^{\prime}=2h-j$より$\displaystyle j^{\prime}=\frac{-a^4+2a^3+1}{a}-\frac{a^2-a+1}{a}=-a^3+2a^2-a+1$である．
以上より示すべきは4点$\displaystyle B(\frac{1}{a^2}),E(\frac{a^2-a+1}{a^2+a+1}),D(\frac{a^3+a^2+1}{a^2+a+1}),I^{\prime}(-a^3+2a^2-a+1)$の共円である．
$\displaystyle\frac{(b-e)(b-d)}{(d-j^{\prime})(e-j^{\prime})}=\frac{\displaystyle(\frac{1}{a^2}-\frac{a^2-a+1}{a^2+a+1})(\frac{1}{a^2}-\frac{a^3+a^2+1}{a^2+a+1})}{\displaystyle(\frac{a^3+a^2+1}{a^2+a+1}-(-a^3+2a^2-a+1))(\frac{a^2-a+1}{a^2+a+1}-(-a^3+2a^2-a+1))}$
これを頑張って計算すると$\displaystyle\frac{a}{a^2+2a+1}$となり,$\displaystyle\overline{\frac{a}{a^2+2a+1}}=\frac{a}{a^2+2a+1}$よりこれは実数である．
したがって4点$B,E,D,I^{\prime}$は同一円周上にある．証明終了

正９角形の外接円の方程式を$|z|=1$とし,$A_9(1),A_1(a)$とすると$i=1,2,\cdots,9$に対して$A_i(a^i)$であり,$a^6+a^3+1=0,a^9=1$・・・※が成り立つ．
$X$は２直線$A_1A_4:z+a^5\overline{z}=a^4+a,A_3A_5:z+a^8\overline{z}=a^5+a^3$の交点だからその座標は※を用いながら計算すると
$\displaystyle\frac{a^7-a^5+a^4-a^3}{a^3-1}$となる．
$Y$は２直線$A_1A_4:z+a^5\overline{z}=a^4+a,A_2A_7:z+\overline{z}=a^7+a^2$の交点だからその座標は※を用いながら計算すると
$\displaystyle\frac{a^7-a^4+a^3-a}{a^5-1}$となる．
よって$\displaystyle X(\frac{a^7-a^5+a^4-a^3}{a^3-1}),Y(\frac{a^7-a^4+a^3-a}{a^5-1}),A_9(1)$より,
$\displaystyle\angle XA_9Y=\arg\frac{\displaystyle \frac{a^7-a^5+a^4-a^3}{a^3-1}-1}{\displaystyle \frac{a^7-a^4+a^3-a}{a^5-1}-1}=\arg\frac{a^5-1}{a^3-1}\cdot\frac{a^7-a^5+a^4-2a^3+1}{a^7-a^5-a^4+a^3-a+1}=\arg\frac{a^5-1}{a^3-1}\cdot\frac{(a-1)^2(a^5+2a^4+2a^3+3a^2+2a+1)}{(a+1)(a-1)^2(a^4+a^3+a^2+1)}$
$=\displaystyle\arg\frac{a^5-1}{a^3-1}-\arg(a+1)+\arg\frac{a^5+2a^4+2a^3+3a^2+2a+1}{a^4+a^3+a^2+1}$　である．
ここで$\displaystyle\arg\frac{a^5-1}{a^3-1}=\angle A_5A_9A_3=40^\circ$であり,$a+1$に対応する点は3点$O,A_1,A_9$と合わせてひし形をなすから$\arg(a+1)=20^\circ$
したがって$\displaystyle\angle XA_9Y=20^\circ+\arg\frac{a^5+2a^4+2a^3+3a^2+2a+1}{a^4+a^3+a^2+1}$となる．
$\displaystyle\frac{a^5+2a^4+2a^3+3a^2+2a+1}{a^4+a^3+a^2+1}=A$とおく．
以下,$\arg A=0^\circ$すなわち$A$が正の実数であることを示す．
※を用いて$A$を$\displaystyle A=\frac{-2a^7-a^6+a^5+a^3+3a^2}{-a^6+a^4+a^2}=\frac{-2a^5-a^4+a^3+a+3}{-a^4+a^2+1}$と変形しておく．
主張1:$A$は実数
　$\displaystyle A=\frac{-2a^5-a^4+a^3+a+3}{-a^4+a^2+1}$の共役複素数$\overline{A}$を$\overline{a^k}=a^{-k}=a^{9-k}$を用いて計算すると
　$\displaystyle\overline{A}=\frac{-2a^4-a^5+a^6+a^8+3a^9}{-a^5+a^7+a^9}=\frac{3a^5+a^4+a^2-a-2}{a^5+a^3-a}$である．
　よって,$\displaystyle A-\overline{A}=\frac{-2a^5-a^4+a^3+a+3}{-a^4+a^2+1}-\frac{3a^5+a^4+a^2-a-2}{a^5+a^3-a}=\frac{(-2a^5-a^4+a^3+a+3)(a^5+a^3-a)-(3a^5+a^4+a^2-a-2)(-a^4+a^2+1)}{(-a^4+a^2+1)(a^5+a^3-a)}$
　※を用いながら分子を計算すると$-4a^7+4a^6-4a^4+4a^3-4a+4=-4(a^6+a^3+1)(a-1)=0$である．
　よって$A-\overline{A}=0$より$A$は実数．
主張2:$A$は正の実数
　$a=\cos40^\circ+i\sin40^\circ$より$k=1,2,\cdots,9$に対して　$a^k=\cos40k^\circ+i\sin40k^\circ$である．
　よって$A$の変形後の分子分母の虚部をそれぞれ計算し,不等式評価をすると
　$Im(-2a^5-a^4+a^3+a+3)=-2\sin200^\circ-\sin160^\circ+\sin120^\circ+\sin40^\circ+3>-2\cdot1-\sin160^\circ+\sin120^\circ+\sin40^\circ+3>0$
　$Im(-a^4+a^2+1)=-\sin160^\circ+\sin80^\circ+1>-1+\sin80^\circ+1>0$
　よって分子分母ともに虚部は正である．したがって分子分母それぞれの偏角は$0^\circ$より大きく$180^\circ$より小さい．
　これと主張1より分子分母の偏角は$180^\circ$を法として合同であることから分子分母の偏角は等しい．よって$A$は特に正の実数．
主張2より$\arg A=0^\circ$であるから$\angle XA_9Y=20^\circ+\arg A=20^\circ$
よって$\angle XA_9Y=20^\circ$　証明終了

三角形$ABC$の外接円の方程式を$|z|=1$とし,$1$に対応する点,$A,B,P,C$はこの順に反時計回りにあるとする．また,弧$AB,AC,BP,CP$(どれも他の点を含まない)の中点をそれぞれ$K,L,M,N$とする．点$A,B,C,P$の座標の偏角($0$から$2\pi$で考える)を半分にし,絶対値を$1$に保った複素数をそれぞれ$a,b,c,p$とする．このとき$A(a^2),B(b^2),C(c^2),P(p^2)$であり,$K(ab),L(-ac),M(bp),N(cp)$となる．
$I_B$は２直線$AM:z+a^2bp\overline{z}=a^2+bp,PK:z+abp^2\overline{z}=ab+p^2$であり,２式より座標を求めると$I_B(-ap+bp+ab)$である．
$I_C$は２直線$AN:z+a^2cp\overline{z}=a^2+cp,PL:z-acp^2\overline{z}=-ac+p^2$であり,２式より座標を求めると$I_C(ap+cp-ac)$である．
これらと$P(p^2)$より三角形$PI_BI_C$の外接円上に点$X(x)(\neq P,I_B,I_C)$がある必要十分条件は
$\displaystyle\frac{(x+ap-bp+ab)(p^2-ap-cp+ac)}{(x-ap-cp+ac)(p^2+ap-bp-ab)}$が実数であることである．$\displaystyle x=\frac{a^2b-a^2c+2abc}{2a-b-c}$とすると,先ほどの数は
$\displaystyle\frac{(\displaystyle\frac{a^2b-a^2c+2abc}{2a-b-c}+ap-bp+ab)(p^2-ap-cp+ac)}{(\displaystyle\frac{a^2b-a^2c+2abc}{2a-b-c}-ap-cp+ac)(p^2+ap-bp-ab)}$これを頑張って計算すると$\displaystyle -\frac{(a-b)(p-a)(p-c)}{(a+c)(p+a)(p+b)}$となり,
$\displaystyle \overline{-\frac{(a-b)(p-a)(p-c)}{(a+c)(p+a)(p+b)}}=\cdots=-\frac{(a-b)(p-a)(p-c)}{(a+c)(p+a)(p+b)}$よりこれは実数．
よって$X(\displaystyle\frac{a^2b-a^2c+2abc}{2a-b-c})$は三角形$PI_BI_C$の外接円上にあり,これは$P$によらない．証明終了
a

内接円の方程式を$|z|=1$とし,$D(a),E(b),F(c)$とする．このとき基本計算より$\displaystyle H(\frac{1}{2}(a+b+c-\frac{bc}{a}))$である．
また,$\displaystyle B(\frac{2ac}{a+c}),C(\frac{2ab}{a+b})$である．これらの点の座標より
$\displaystyle\angle HCE=\arg\frac{\displaystyle\frac{2ab}{a+b}-\frac{1}{2}(a+b+c-\frac{bc}{a}}{\displaystyle\frac{2ab}{a+b}-b}$これを計算して
$\displaystyle\angle HCE=\arg-\frac{a^2-ab+ac+bc}{2ab}$となる．同様に$\displaystyle\angle HBF=\arg-\frac{a^2+ab-ac+bc}{2ac}$である．
よって$\displaystyle\angle HCE+\angle HBF=\frac{(a^2-ab+ac+bc)(a^2+ab-ac+bc)}{4a^2bc}$である．右辺について
$\displaystyle\overline{\frac{(a^2-ab+ac+bc)(a^2+ab-ac+bc)}{4a^2bc}}=\frac{\displaystyle(\frac{1}{a^2}-\frac{1}{ab}+\frac{1}{ac}+\frac{1}{bc})(\frac{1}{a^2}+\frac{1}{ab}-\frac{1}{ac}+\frac{1}{bc})}{\displaystyle\frac{4}{a^2bc}}=\frac{(a^2+ab-ac+bc)(a^2-ab+ac+bc)}{4a^2bc}$
よって右辺は実数であるから$\angle HCE+\angle HBF$は$180^\circ$の整数倍．明らかに$\ -180^\circ<\angle HCE+\angle HBF<180^\circ$だから$\angle HCE+\angle HBF=0^\circ$
よって$|\angle HCE|=|\angle HBF|$だから$|\angle KBL|=|\angle KCL|$がいえ,円周角の定理の逆より$B,C,K,L$は同一円周上にある．証明終了

$\Omega:|z|=1,A_1(a),B_1(b),C_1(c),T(t)$とする．点$A$は線分$TB_1,TC_1$の垂直二等分線の交点である．
$TB_1$の垂直二等分線の方程式を求めると$\displaystyle(\overline{t}-\frac{1}{b})z+(t+b)\overline{z}=|t|^2-1$
同様に$TC_1$の垂直二等分線の方程式は$\displaystyle(\overline{t}-\frac{1}{c})z+(t+c)\overline{z}=|t|^2-1$
2式より$A$の座標を求めると$\displaystyle A(bc\cdot\frac{|t|^2-1}{t+bc\overline{t}-b-c})$となる．
ここで,基本計算より$\displaystyle A_2(\frac{a-t}{a\overline{t}-1})$である．これと$\displaystyle A(bc\cdot\frac{|t|^2-1}{t+bc\overline{t}-b-c})$より
直線$AA_2$と$\Omega$が再び交わる点の座標は基本計算より,
$\displaystyle\frac{\displaystyle\frac{a-t}{a\overline{t}-1}-bc\cdot\frac{|t|^2-1}{ t+bc\overline{t}-b-c}}{\displaystyle\frac{a-t}{a\overline{t}-1}\cdot\frac{|t|^2-1}{t+bc\overline{t}-b-c}-1}$これを頑張って計算すると
$\displaystyle\frac{abc|t|^2\overline{t}+t^2-(a+b+c)t+2abc\overline{t}+ab+bc+ca}{t|t|^2+abc\overline{t}^2-2t-(ab+bc+ca)\overline{t}+a+b+c}$　となる．
これは$a,b,c$について対称であるから,直線$BB_2,CC_2$と$\Omega$が再び交わる点の座標も全く同じ座標である．
したがって直線$AA_2,BB_2,CC_2$は$\Omega$上の一点で交わる．証明終了
a

$A(a),B(b),C(c)　(|a|,|b|,|c|=1)$とすると$\displaystyle M(\frac{b+c}{2}),H(a+b+c)$である．
直線$AM$の方程式は$(\overline{a}-\overline{m})z-(a-m)\overline{z}=\overline{a}m-a\overline{m}$　これを計算すると,
$AM:(ab+ac-2bc)z+abc(2a-b-c)\overline{z}=a^2b+a^2c-b^2c-bc^2$　となる．これに垂直で$H$を通る直線の方程式を求めると
$(ab+ac-2bc)z-abc(2a-b-c)\overline{z}=-a^2b-a^2c+2ab^2+2ac^2-b^2c-bc^2$　
これと$AM$の交点が$P$だから2式より$P$の座標は$\displaystyle\frac{ab^2+ac^2-b^2c-bc^2}{ab+ac-2bc}$である．
3点$A,P,M$はこの順に並んでいるから
$AM\cdot PM=\overline{a-m}\cdot(p-m)=\displaystyle\frac{2bc-ab-ac}{2abc}\cdot\frac{ab^2+ac^2-2abc}{2(ab+ac-2bc)}=-\frac{(b-c)^2}{4bc}$
また,$BM^2=(b-m)\cdot\overline{b-m}=\displaystyle\frac{b-c}{2}\cdot\frac{c-b}{2bc}=-\frac{(b-c)^2}{4bc}$
よって$AM\cdot PM=BM^2$である．証明終了

三角形$ABC$の外接円の方程式を$|z|=1$とし,$A(a),B(b),C(c)$とする．$0< s,t<1$として点$D,E$が辺$AB,AC$をそれぞれ$s:1-s,t:1-t$に内分しているとすると$D((1-s)a+sb),E((1-t)a+tc)$である．
線分$BD$の垂直二等分線は$AB$に垂直で,線分$BD$の中点(座標は$\displaystyle\frac{1}{2}((1-s)a+(1+s)b)$である)を通るから
その方程式を求めると$z-ab\overline{z}=-sa+sb$となる．
同様に線分$CE$の垂直二等分線の方程式は$z-ac\overline{z}=-ta+tc$である．2式から交点$K$の座標を求めると
$K(\displaystyle\frac{-(s-t)bc-tab+sac}{b-c})$である．
ここで$\angle MFL$は直線$DE$が直線$BC$となす角と等しいから
$\displaystyle\angle MFL=\arg\frac{e-d}{c-b}=\arg\frac{-(s-t)a+sb-tc}{c-b}$である．
また,$\displaystyle\angle LOM=\angle KOA=\arg\frac{k}{a}=\arg\frac{-(s-t)bc-tab+sac}{a(b-c)}$である．よって
$\displaystyle\angle MFL+\angle LOM=\arg\frac{(-(s-t)a+sb-tc)(-(s-t)bc-tab+sac)}{a(b-c)(c-b)}$
右辺について$\displaystyle\frac{(-(s-t)a+sb-tc)(-(s-t)bc-tab+sac)}{a(b-c)(c-b)}=\frac{-(s-t)a+sb-tc}{b-c}\cdot\frac{\displaystyle-\frac{s-t}{a}+\frac{s}{b}-\frac{t}{c}}{\displaystyle\frac{1}{b}-\frac{1}{c}}=\frac{-(s-t)a+sb-tc}{b-c}\cdot\overline{\frac{-(s-t)a+sb-tc}{b-c}}$よりこれは実数である．これと$0^\circ<\angle MFL+\angle LOM<360^\circ$より$\angle MFL+\angle LOM=180^\circ$
よって4点$F,M,L,O$は同一円周上にある．証明終了
a

$\omega$の方程式を$|z|=1$とし,$\omega$と辺$BC,CA,AB$の接点をそれぞれ$D(a),E(b),F(c)$とする．
このとき$\displaystyle A(\frac{2bc}{b+c}),BC:z+a^2\overline{z}=2a$より$A$から$BC$へおろした垂線の方程式は$\displaystyle z-a^2\overline{z}=\frac{2(bc-a^2)}{b+c}$である．またこれと$\omega:z\overline{z}=1$を考えると,$z=p_1,p_2$はこの2つの方程式を満たす．2つの方程式から$\overline{z}$を消去して,整理すると2次方程式$(b+c)z^2+2(a^2-bc)z-a^2(b+c)$となるから解と係数の関係より$\displaystyle p_1+p_2=-\frac{2(a^2-bc)}{b+c},p_1p_2=-a^2$を得る．
よってこれらの式を用いて$Q_1$の座標は$\displaystyle\frac{2p_1p_2}{p_1+p_2}=\frac{a^2(b+c)}{2(a^2-bc)}$である．
$a,b,c$の対称性より同様に$\displaystyle Q_2(\frac{b^2(c+a)}{2(b^2-ca)}),Q_3(\frac{c^2(a+b)}{2(c^2-ab)})$を得る．
ここで$\displaystyle\frac{q_1-q_2}{q_1-q_3}=\frac{\displaystyle\frac{a^2(b+c)}{2(a^2-bc)}-\frac{b^2(c+a)}{2(b^2-ca)}}{\displaystyle\frac{a^2(b+c)}{2(a^2-bc)}-\frac{c^2(a+b)}{2(c^2-ab)}}$を計算すると$\displaystyle\frac{(b-a)(c^2-ab)}{(c-a)(b^2-ca)}$となり,$\displaystyle\overline{\frac{(b-a)(c^2-ab)}{(c-a)(b^2-ca)}}=\frac{(b-a)(c^2-ab)}{(c-a)(b^2-ca)}$であるから$\displaystyle\frac{q_1-q_2}{q_1-q_3}$は実数．したがって$Q_1,Q_2,Q_3$は同一直線上にある．証明終了

三角形$ABC$の外接円の方程式を$|z|=1$とし,$A(a),B(b),C(c)$とする．また,$\displaystyle P(\frac{ab+bc+ca}{a+b+c})$とする．
　$O(0)$より,$O_2(a+c),O_3(a+b)$である．このとき
$\displaystyle\frac{(p-(a+b))((a+c)-a)}{(p-(a+c))((a+b)-a)}=\frac{c((ab+bc+ca)-(a+b)(a+b+c))}{b((ab+bc+ca)-(a+c)(a+b+c))}=\frac{c(a^2+ab+b^2)}{b(a^2+ac+c^2)}$
となり,$\displaystyle\overline{\frac{c(a^2+ab+b^2)}{b(a^2+ac+c^2)}}=\cdots=\frac{c(a^2+ab+b^2)}{b(a^2+ac+c^2)}$より
$\displaystyle\frac{(p-(a+b))((a+c)-a)}{(p-(a+c))((a+b)-a)}$は実数．したがって三角形$O_2O_3A$の外接円は$P$を通る．
$a,b,c$の対称性より三角形$O_1O_2C,O_1O_3B$の外接円も$P$を通る．
　$\displaystyle G(\frac{1}{3}(a+b+c))$から辺$AB$に下ろした垂線の方程式を求めると$\displaystyle z-ab\overline{z}=\frac{1}{3}(c^2-ab)$
これと$AB:z+ab\overline{z}=a+b$より2直線の交点の座標を求めると$\displaystyle\frac{1}{6}(3a+3b+c-\frac{ab}{c})$となる．
これは$GG_3$の中点であるから$\displaystyle g_3=2\cdot\frac{1}{6}(3a+3b+c-\frac{ab}{c})-\frac{1}{3}(a+b+c)=\frac{1}{3}(2a+2b-\frac{ab}{c})$が得られる．
同様に$\displaystyle g_2=\frac{1}{3}(2a+2c-\frac{ac}{b})$である．このとき
$\displaystyle\frac{(g_3-p)(a-g_2)}{(g_2-p)(a-g_3)}=\frac{\displaystyle(\frac{1}{3}(2a+2b-\frac{ab}{c})-\frac{ab+bc+ca}{a+b+c})(a-\frac{1}{3}(2a+2c-\frac{ac}{b}))}{\displaystyle(\frac{1}{3}(2a+2c-\frac{ac}{b})-\frac{ab+bc+ca}{a+b+c})(a-\frac{1}{3}(2a+2b-\frac{ab}{c}))}$を
頑張って計算すると$\displaystyle\frac{a^2b-2a^2c+ab^2+ac^2-ab^2c+bc^2}{a^2c-2a^2b+ab^2+ac^2-abc^2+b^2c}$となり,
$\displaystyle\overline{\frac{a^2b-2a^2c+ab^2+ac^2-ab^2c+bc^2}{a^2c-2a^2b+ab^2+ac^2-abc^2+b^2c}}=\cdots=\frac{a^2b-2a^2c+ab^2+ac^2-ab^2c+bc^2}{a^2c-2a^2b+ab^2+ac^2-abc^2+b^2c}$
より$\displaystyle\frac{(g_3-p)(a-g_2)}{(g_2-p)(a-g_3)}$は実数．したがって三角形$G_2G_3A$の外接円は$P$を通る．
$a,b,c$の対称性より三角形$G_1G_2C,G_1G_3B$の外接円も$P$を通る．
　また,$\displaystyle\overline{p}=\frac{a+b+c}{ab+bc+ca}=\frac{1}{p}$より$|p|=1$だから三角形$ABC$の外接円は$P$を通る．
以上より三角形$G_1G_2C,G_1G_3B,G_2G_3A,O_1O_2C,O_1O_3B,O_2O_3A,ABC$それぞれの外接円は共通の点$P$を通る．証明終了．

辺$BC,AB,AC$と$\omega$の接点をそれぞれ$D,E,F$とする．$\omega$の方程式を$|z|=1$,$D(a),E(b),F(c)$ $(b,c$は互いに共役$)$と複素座標を設定する．
このとき$bc=1,b+c=s$ $(s$は実数$)$となり,
$BC:z+a^2\overline{z}=2a,AB:z+b^2\overline{z}=2b,AC:z+c^2\overline{z}=2c$　より
点$A,B,C$の座標は$\displaystyle A\left(\frac{2}{s}\right),B\left(\frac{2ab}{a+b}\right),C\left(\frac{2ac}{a+c}\right)$　となる,
したがって点$M$の座標は$\displaystyle m=\frac{1}{2}\left(\frac{2ab}{a+b}+\frac{2ac}{a+c}\right)=\frac{sa^2+2a}{a^2+sa+1}$　である．
直線$AI$は実軸に一致するから,それに垂直な直線で,点$M$を通るもの(すなわち$MK$)の方程式は,
$\displaystyle z+\overline{z}=\frac{sa^2+2a}{a^2+sa+1}+\overline{\left(\frac{sa^2+2a}{a^2+sa+1}\right)}=\frac{sa^2+4a+s}{a^2+sa+1}$
すなわち$\displaystyle MK:z+\overline{z}=\frac{sa^2+4a+s}{a^2+sa+1}$　である．
一方で,点$A$を通り直線$BC(:z+a^2\overline{z}=2a)$に垂直な直線すなわち$(AK)$の方程式は
$\displaystyle z-a^2\overline{z}=\frac{2}{s}(1-a^2)$　である．直線$MK,AK$の式から$z$を求めるとそれが点$K$の座標だから実際に求めると,$\displaystyle k=\frac{(s^2-2)a^2+2sa+2}{s(a^2+sa+1)}$,また,$\displaystyle \overline{k}=\frac{2a^2+2sa+(s^2-2)}{s(a^2+sa+1)}$　である．
簡単のために$(s^2-2)a^2+2sa+2=p,2a^2+2sa+(s^2-2)=q,a^2+sa+1=r$とすると,
$\displaystyle k=\frac{p}{sr},\overline{k}=\frac{q}{sr}$となる．
　線分$AK$を直径とする円と$\omega$の交点を$X$とする．このとき$|x|=1$より$\displaystyle\overline{x}=\frac{1}{x}　…(*)$
$\angle AXK=90^{\circ}$より,$\displaystyle\frac{x-\displaystyle\frac{2}{s}}{x-k}$は純虚数．よって,途中に$(*)$を用いて
$\displaystyle\frac{x-\displaystyle\frac{2}{s}}{x-k}+\overline{\left(\frac{x-\displaystyle\frac{2}{s}}{x-k}\right)}=\frac{x-\displaystyle\frac{2}{s}}{x-k}+\frac{\overline{x}-\displaystyle\frac{2}{s}}{\overline{x}-\overline{k}}=\frac{x-\displaystyle\frac{2}{s}}{x-\displaystyle\frac{p}{sr}}+\frac{\displaystyle\frac{1}{x}-\frac{2}{s}}{\displaystyle\frac{1}{x}-\frac{q}{sr}}$
　　　　　　　　　　　$=\displaystyle r\left(\frac{sx-2}{srx-p}+\frac{2x-s}{qx-sr}\right)=0$
よって分母を払って,$s(q+2r)x^2-(s^2r+2q+2q)x+s(p+2r)$と,$x$の2次方程式が得られる．
$p,q,r$を$s,a$に戻して変形すると$s\left((2a+s)z-(sa+2)\right)^2$となる．
これは線分$AK$を直径とする円と$\omega$の交点がちょうど1つであることを意味するから2つの円は接することが示された．
図 　証明終了

$\omega:|z|=1$とし,$D(a),E(b),F(c)$とする．このとき$\displaystyle A(\frac{2bc}{b+c}),B(\frac{2ac}{a+c}),C(\frac{2ab}{a+b})$である．
$\displaystyle R(-\frac{bc}{a})$より$P$の座標は$\displaystyle\frac{\displaystyle -\frac{bc}{a}-\frac{2bc}{b+c}}{\displaystyle -\frac{bc}{a}\cdot\frac{2}{b+c}-1}=\cdots=\frac{bc(2a+b+c)}{ab+ac+2bc}$である．
よって線分$PE$の垂直二等分線の方程式は$\displaystyle z-\frac{b^2c(2a+b+c)}{ab+ac+2bc}\overline{z}=0$
また,線分$CF$の垂直二等分の方程式は$\displaystyle z-b^2\overline{z}=\frac{1}{2}(b+\frac{2ab}{a+b})-b^2\cdot\frac{1}{2}(\frac{1}{b}+\frac{2}{a+b})=\frac{a(a-b)}{a+b}$となる．
2式より三角形$PCE$の外心($O_c$とおく)の座標は$\displaystyle -\frac{bc(a-b)(2a+b+c)}{(a+b)(a+c)(b-c)}$である．同様に$b,c$を入れ替えて三角形$PBF$の外心($O_b$とおく)の座標は$\displaystyle \frac{bc(a-c)(2a+b+c)}{(a+b)(a+c)(b-c)}$である．
ここで直線$PQ$は$O_bO_c$に垂直な直線だからその方程式の左辺は$\displaystyle z+\frac{O_b-O_c}{\overline{O_b-O_c}}\overline{z}$とおける．
$\displaystyle O_b-O_c=\frac{bc(2a-b-c)(2a+b+c)}{(a+b)(a+c)(b-c)},\overline{O_b-O_c}=-\frac{(ab+ac-2bc)(ab+ac+2bc)}{bc(a+b)(a+c)(b-c)}$より$\displaystyle\frac{O_b-O_c}{\overline{O_b-O_c}}=\frac{b^2c^2(2a-b-c)(2a+b+c)}{(ab+ac-2bc)(ab+ac+2bc)}$である．これと,右辺は$z=p$を代入すると得られることから
$\displaystyle PQ:z+\frac{b^2c^2(2a-b-c)(2a+b+c)}{(ab+ac-2bc)(ab+ac+2bc)}\overline{z}=p+\frac{b^2c^2(2a-b-c)(2a+b+c)}{(ab+ac-2bc)(ab+ac+2bc)}\overline{p}=\frac{bc(2a+b+c)}{ab+ac+2bc}+\frac{bc(2a-b-c)}{ab+ac-2bc}$
分母を払って整理すると$(ab+ac-2bc)(ab+ac+2bc)z+b^2c^2(2a-b-c)(2a+b+c)\overline{z}=4bc(b+c)(a^2-bc)$
これと$DI:z-a^2\overline{z}=0$を連立して$DI,PQ$の交点($X$とおく)の座標を求めると
$\displaystyle\frac{4a^2bc}{(a^2+bc)(b+c)}$となる．このとき
$\displaystyle\frac{\displaystyle\frac{4a^2bc}{(a^2+bc)(b+c)}-\frac{2bc}{b+c}}{\displaystyle\frac{2bc}{b+c}}=\frac{a^2-bc}{a^2+bc}$であり,
$\displaystyle\overline{\frac{a^2-bc}{a^2+bc}}=\cdots=-\frac{a^2-bc}{a^2+bc}$よりこれは純虚数．
すなわち$\angle IAX$は直角．証明終了

三角形$ABC$の外接円の方程式を$|z|=1$とする．このときうまく複素数$a,b,c$を定めると$A(a^2),B(b^2),C(c^2),I(-ab-ac-bc)$と表せる．このとき直線$ID$の方程式は$\displaystyle z-b^2c^2\overline{z}=-ab-ac+\frac{b^2c}{a}+\frac{bc^2}{a}$　であり,これに垂直で点$O(0)$を通る直線$OP$の方程式は$z+b^2c^2\overline{z}=0$　である．これら2式から$z$を求めることで点$P$の座標が求まるから,$p=\displaystyle\frac{1}{2}(-ab-ac+\frac{b^2c}{a}+\frac{bc^2}{a})$　となる．ここで線分$AA^{\prime}$の中点は$p$に等しいから,$\displaystyle a^2+a^{\prime}=2p=-ab-ac+\frac{b^2c}{a}+\frac{bc^2}{a}$よって$\displaystyle a^{\prime}=-a^2-ab-ac+\frac{b^2c}{a}+\frac{bc^2}{a}$
同様にして$\displaystyle b^{\prime}=-b^2-ab-bc+\frac{a^2c}{b}+\frac{ac^2}{b}$,$\displaystyle c^{\prime}=-c^2-ac-bc+\frac{a^2b}{c}+\frac{ab^2}{c}$　を得る．三角形$A^{\prime}B^{\prime}C^{\prime}$の外接円と三角形$ABC$の外接円の交点を$x$とおくと,$\overline{x}=\displaystyle\frac{1}{x}$　であり,$\displaystyle\frac{(x-b^{\prime})(c^{\prime}-a^{\prime})}{(x-c^{\prime})(b^{\prime}-a^{\prime})}$　(これを$X$とおく)は実数である．
$X$を計算すると$\displaystyle X=\frac{bx-ca^2+(b^2-c^2)a+b^3+b^2c}{cx-ba^2+(c^2-b^2)a+c^3+bc^2}\cdot\frac{a-c}{a-b}$である．さらに$\overline{x}=\displaystyle\frac{1}{x}$も用いながら$\overline{X}$を計算すると$\displaystyle\overline{X}=\frac{\lbrace (bc+c^2)a^2-(b^3-bc^2)a-b^3c \rbrace x+a^2b^2c^2}{\lbrace (bc+b^2)a^2-(c^3-b^2c)a-bc^3 \rbrace x+a^2b^2c^2}\cdot\frac{a-c}{a-b}$である．$X$は実数であったから$X=\overline{X}$であり,$\displaystyle\frac{bx-ca^2+(b^2-c^2)a+b^3+b^2c}{cx-ba^2+(c^2-b^2)a+c^3+bc^2}=\displaystyle\frac{\lbrace (bc+c^2)a^2-(b^3-bc^2)a-b^3c \rbrace x+a^2b^2c^2}{\lbrace (bc+b^2)a^2-(c^3-b^2c)a-bc^3 \rbrace x+a^2b^2c^2}$
が従う．この式の分母を払って整理すると$(*)$,次の$x$についての2次方程式が得られる．
$(a^2+b^2+c^2+2ab+2bc+2ca)x^2-2(a^2b+a^2c+b^2c+b^2a+c^2a+c^2b+3abc)x$
　　　　　　　　　　　　　　　$+(a^2b^2+b^2c^2+c^2a^2+2a^2bc+2ab^2c+2abc^2)=0$
これは$\lbrace (a+b+c)x-(ab+bc+ca) \rbrace^2=0$　と変形できるからこの方程式の解は1つである．すなわち三角形$A^{\prime}B^{\prime}C^{\prime}$の外接円と三角形$ABC$の外接円の交点はただ1つであり,これはこの2つの円が接することを意味する．証明終了．

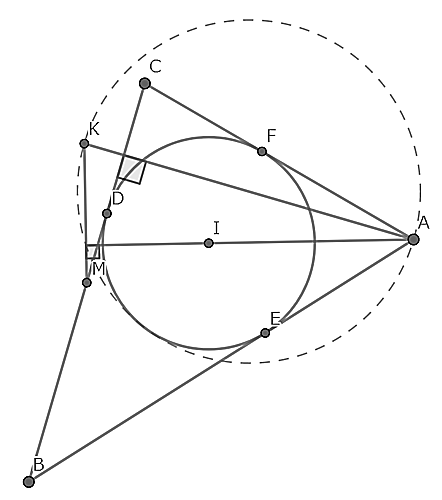
$MB^2=MB^2=MI^2=MA\cdot MD=MK\cdot MS$・・・※は有名な事実なので証明略とする．
よって点$M$を中心とした半径$MI$の反転をすると,$B,C,I$は不変,$A$と$D$,$K$と$S$は互いに移りあう．以下,"反転"というとこの反転のことをいうとする．また,4点$A,D,K,S$は同一円周上にあるから$\angle MAS=\angle MKD=90^\circ$である．
$M(0),B(b),C(c)　(Re(b)=Re(c)=k),I(a)　(|a|=|b|=|c|=1)$とすると,反転によって点$X(x)$は点$\displaystyle X^\prime(\frac{1}{\overline{z}})$に移る．
また,$bc=1,b+c=2k$が成り立つ．
反転によって$N$が移る点を$N^\prime$とすると反転によって三角形$KID$の外接円は三角形$SIA$の外接円に移り,三角形$MAN$の外接円は直線$DN^\prime$に移る．したがって,三角形$SIA$の外接円と直線$DN^\prime$の交点(2点まとめて$L^\prime$とおく)を求め,そこから$L$の座標がわかるので,このように計算を進めていく．
$BC:z+\overline{z}=2k,MI:z-a^2\overline{z}=0$より交点を求めて$\displaystyle D(\frac{2ka^2}{a^2+1})$である．
反転によって$D$は$A$に移るから$A$の座標は$\displaystyle\frac{1}{\overline{d}}=\frac{a^2+1}{2k}$である,
$A$を通って直線$MI$に垂直な直線の方程式を求めると$\displaystyle z+a^2\overline{z}=\frac{a^2+1}{k}$であり,
これと$BC:z+\overline{z}=2k$の交点が$S$だから座標を求めると$\displaystyle S(\frac{2k^2a^2-a^2-1}{k(a^2-1)})$となる．
したがって$N$の座標は$\displaystyle\frac{1}{2}(a+\frac{2k^2a^2-a^2-1}{k(a^2-1)})=\frac{(a^2+2ka+1)(ka-1)}{2k(a^2-1)}$となる．
よって$N^\prime$の座標は$\displaystyle\frac{1}{\overline{n}}=\frac{2ka(a^2-1)}{(a^2+2ka+1)(a-k)}$である．直線$DN^\prime$の方程式を求める．
$d-n^\prime,\overline{d-n^\prime},\displaystyle\frac{d-n^\prime}{\overline{d-n^\prime}}$の順に計算すると,$\displaystyle\frac{d-n^\prime}{\overline{d-n^\prime}}=\frac{(ka+1)(1-ka)}{(a-k)(a+k)}$であるから,
$\displaystyle DN^\prime=z-\frac{(ka+1)(1-ka)}{(a-k)(a+k)}\overline{z}=\cdots=\frac{2k(a^2-1)}{(a^2-k^2)}$となる．
よって$L^\prime(l^\prime)$は$\displaystyle l^\prime-\frac{(ka+1)(1-ka)}{(a-k)(a+k)}\overline{l^\prime}=\frac{2k(a^2-1)}{(a^2-k^2)}$を満たす．よって$\displaystyle\overline{l^\prime}=-\frac{a^2-k^2}{k^2a^2-1}+\frac{2k(a^2-1)}{k^2a^2-1}$である．
三角形$SIA$の外接円上に$L^\prime(l^\prime)$があるから,
$\displaystyle\frac{\displaystyle (l^\prime-a)(\frac{2k^2a^2-a^2-1}{k(a^2-1)}-\frac{a^2+1}{2k})}{\displaystyle (l^\prime-\frac{a^2+1}{2k})(\frac{2k^2a^2-a^2-1}{k(a^2-1)}-a)}$は実数．整理して,$\displaystyle\frac{k(a^2+2ka+1)}{a}$が実数(証明略)を用いると,
$\displaystyle\frac{l^\prime-a}{2kl^\prime-(a^2+1)}\cdot\frac{a}{ka+1}$は実数となる．したがって
$\displaystyle\frac{l^\prime-a}{2kl^\prime-(a^2+1)}\cdot\frac{a}{ka+1}=\overline{\frac{l^\prime-a}{2kl^\prime-(a^2+1)}\cdot\frac{a}{ka+1}}=\frac{a\overline{l^\prime}-1}{2ka^2\overline{l^\prime}-(a^2+1)}\cdot\frac{1}{a+k}$である．
分母を払って頑張って整理すると$2k(a^2-1)l^\prime\overline{l^\prime}-(a-k)(a^2+2ka+1)l^\prime-a(ka-1)(a^2+2ka+1)\overline{l^\prime}-(a^4-1)$となる．
$\displaystyle\overline{l^\prime}=-\frac{a^2-k^2}{k^2a^2-1}+\frac{2k(a^2-1)}{k^2a^2-1}$を代入して頑張って整理すると
$2ka(a+k)(a-k)l^{\prime 2}-(ka^4+5k^2a^3-a^3-2k^3a^2-3k^2a-a+k)l^\prime+(ka-1)(ka^3+4k^2a^2-a^2+ka-1)$となり,これは
$\lbrace(a-k)l^\prime-(ka-1)\rbrace\lbrace 2ka(a+k)l^\prime-(ka^3+4k^2a^2-a^2+ka-1)\rbrace$と因数分解できるから$\displaystyle l^\prime=\frac{ka-1}{a-k}$または$\displaystyle l^\prime=\frac{ka^3+4k^2a^2-a^2+ka-1}{2ka(a+k)}$である．
$\displaystyle l^\prime=\frac{ka-1}{a-k}$とすると,$\displaystyle l=\frac{1}{\overline{l^\prime}}=\frac{ka-1}{a-k}$より
$\displaystyle L(\frac{ka-1}{a-k})$である．これと$I(a)$の中点($W$とおく)の座標は$\displaystyle\frac{a^2-1}{2(a-k)}$であり,この点を反転すると座標は$\displaystyle \frac{1}{\overline{\displaystyle\frac{a^2-1}{2(a-k)}}}=\frac{2a(ka-1)}{a^2-1}$である．
ここで$\displaystyle\frac{2a(ka-1)}{a^2-1}+\overline{\frac{2a(ka-1)}{a^2-1}}=2k$より$W$の反転先は直線$BC$上にある．直線$BC$は$\Omega$の反転先であることから元の点$W$は$\Omega$上にある．これが示したいことであった．証明終了
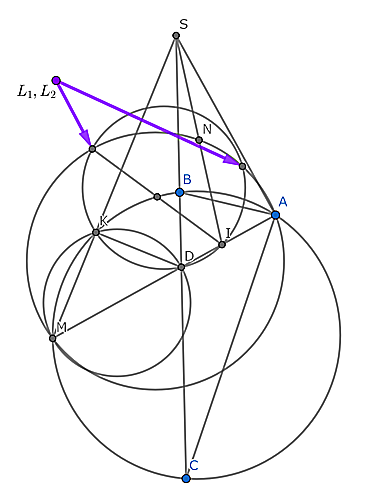a

三角形$ABC$の内接円の方程式を$|z|=1$とし,内接円と辺$BC,CA$の接点を$H(a),J(b)$,また,$F(c)$とする．このとき$\displaystyle A(\frac{2bc}{b+c}),B(\frac{2ac}{a+c}),C(\frac{2ab}{a+b})$であり,$M$の座標は$\displaystyle\frac{1}{2}(\frac{2ac}{a+c}+\frac{2ab}{a+b})=\frac{a(ab+ac+2bc)}{(a+b)(a+c)}$である．
辺$BC$の垂直二等分線の方程式を求めると$\displaystyle z-a^2\overline{z}=-\frac{2a(a^2-bc)}{(a+b)(a+c)}$
また,$\angle BAC$の二等分線の方程式を求めると$z-bc\overline{z}=0$である．この2直線の交点が$E$であるから座標を求めると,
$\displaystyle E(\frac{2abc}{(a+b)(a+c)})$である．
また,$A$を通り$BC$に平行な直線の方程式は$\displaystyle z+bc\overline{z}=\frac{4bc}{b+c}$　これと辺$BC$の垂直二等分線の方程式$\displaystyle z-a^2\overline{z}=-\frac{2a(a^2-bc)}{(a+b)(a+c)}$　よりこの2直線の交点が$D$であるから座標を求めると,
$\displaystyle D(\frac{2abc(2a+b+c)}{(a+b)(a+c)(b+c)})$である．
また,辺$BC$の垂直二等分線の方程式$\displaystyle z-a^2\overline{z}=-\frac{2a(a^2-bc)}{(a+b)(a+c)}$と$BC:z+a^2\overline{z}=2a$よりこの2直線の交点が$G$であるから,座標を求めると,$\displaystyle G(\frac{2abc}{a^2+bc})$である．
また,$B$を通り$AB$に垂直な直線の方程式は$\displaystyle z-c^2\overline{z}=\frac{2c(a-c)}{a+c}$であり,さらに,
直線$EF$の方程式を頑張って求めると,$(a^2+ab-ac+bc)z-c^2(a^2-ab+ac+bc)\overline{z}=2ac(b-c)$である．
この2直線の交点が$N$であるから座標を求めると$\displaystyle N(-\frac{c(a^3-2a^2b+a^2c+abc-bc^2)}{a(a+c)(b-c)})$となる．
ここで簡単な角度計算より$NB$が$EM$となす角は$BF$が$BH$となす角に等しく,これと$NB=EM,BF=BH$より,
$\displaystyle\frac{\displaystyle n-\frac{2ac}{a+c}}{e-m}=\frac{\displaystyle \frac{2ac}{a+c}-c}{\displaystyle \frac{2ac}{a+c}-a}=-\frac{c}{a}$
最左辺$\displaystyle=\frac{\displaystyle -\frac{c(a^3-2a^2b+a^2c+abc-bc^2)}{a(a+c)(b-c)}-\frac{2ac}{a+c}}{\displaystyle\frac{2abc}{(a+b)(a+c)}-\frac{a(ab+ac+2bc)}{(a+b)(a+c)}}$
これを頑張って計算すると$\displaystyle\frac{c(a+b)(a-c)(a^2+bc)}{a^3(b+c)(b-c)}$　これが$\displaystyle -\frac{c}{a}$に等しいから
$\displaystyle -\frac{(a+b)(a-c)(a^2+bc)}{a^2(b+c)(b-c)}=1$が得られる．
　さて,三角形$BFD,EGD$が相似であることと$\displaystyle\frac{\displaystyle\frac{2ac}{a+c}-d}{\displaystyle\frac{2ac}{a+c}-f}=\frac{e-d}{e-g}$であることは同値である．
左辺$\displaystyle=\frac{\displaystyle\frac{2ac}{a+c}-\frac{2abc(2a+b+c)}{(a+b)(a+c)(b+c)}}{\displaystyle\frac{2ac}{a+c}-c}=\cdots=-\frac{2a^2(b-c)}{(a+b)(b+c)(a-c)}$
右辺$\displaystyle=\frac{\displaystyle\frac{2abc}{(a+b)(a+c)}-\frac{2abc(2a+b+c)}{(a+b)(a+c)(b+c)}}{\displaystyle\frac{2abc}{(a+b)(a+c)}-\frac{2abc}{a^2+bc}}=\cdots=\frac{2(a^2+bc)}{(b+c)^2}$
よって三角形$BFD,EGD$が相似$\Longleftrightarrow\displaystyle -\frac{2a^2(b-c)}{(a+b)(b+c)(a-c)}=\frac{2(a^2+bc)}{(b+c)^2}$
$\Longleftrightarrow\displaystyle -\frac{(a+b)(a-c)(a^2+bc)}{a^2(b+c)(b-c)}=1$これは先ほど$BN=EM$より得られた等式より成立する．
よって三角形$BFD,EGD$は相似だから$\angle AFD=\angle AGD$が得られ,4点$A,F,G,D$は同一円周上にある．
よって$\angle DFG=\angle DAG=90^\circ$より$DF$は$FG$に垂直．証明終了
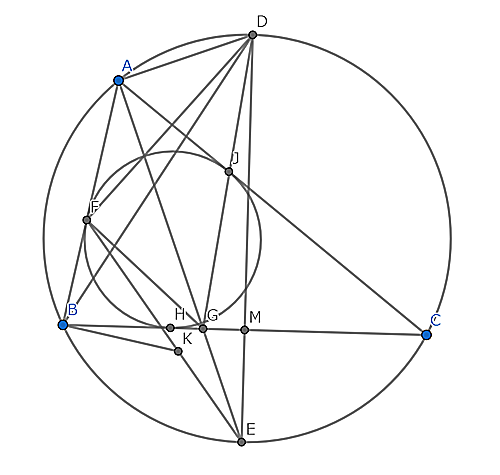図