5
解説大学数学以上
元日算額解説〜壱の巻〜
693
5
$$$$
こんにちは、UFDです。
今回は1月1日に数学を愛する会のTwitterで紹介された自作問題の解説を行います。↓そのtweet
https://twitter.com/mathlava/status/1344931558717857792?s=20
この問題です。
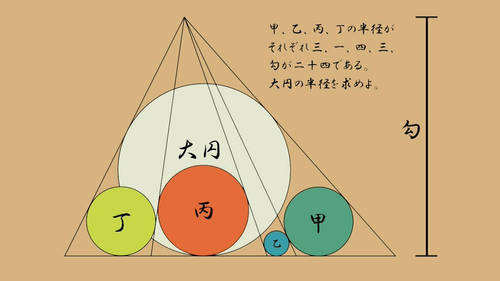問題
正月ということで和算をイメージした問題になっています。
まだ解いていない方は是非解いてみてください。
また、解説が長いのでいくつかの章に分けることにしました。
これは第一章です。
では、始めます。
まず次の補題1を示します。
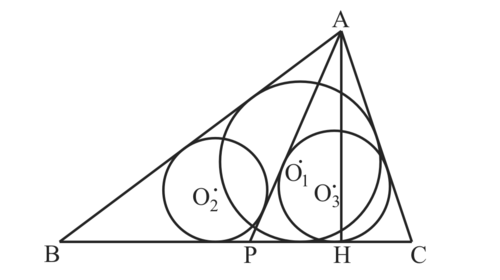
$図1$のように$3円O_1, O_2, O_3$はそれぞれ$△ABC, △ABP, △APC$の内接円とする。$また、頂点Aから辺BC$に下ろした垂線の$足をHとする。$$このとき、 円 O_1, O_2, O_3$の半径を$それぞれ r_1, r_2, r_3とし、$$AH = h とするとき、$
$h(r_2+r_3-r_1)-2r_2r_3=0$
である。
画像1
【補題1の証明】
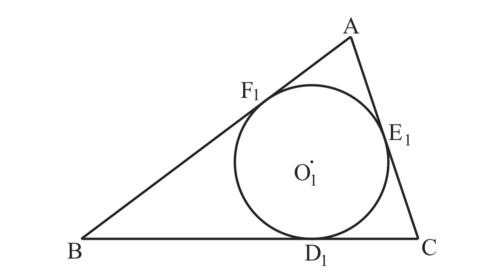
$図 2$の$ように、3 辺 BC, CA, AB$の$長さをそれぞれ a, b, c とし、$
$s =\frac{a+b+c}{2} $とする。
画像2
$また、内接円 O_1 が 3 辺 BC, CA, AB と接する点を$
$それぞれ D_1, E_1, F_1 とし、AF_1 = α, BD_1 = β, CE_1 = γ とする。$
このとき、$ β = s−b, γ = s−a である。$
次に、$図3$のように、
$辺BCと2円O_2, O_3$の$接点をそれぞれ D_2, D_3 とする。$
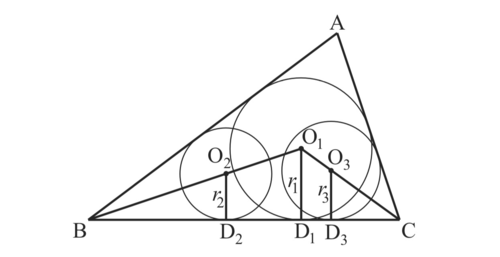図3
$△O_1BD_1 と △O_2BD_2 は相似なので、$
$BD_1 :BD_2 =β:BD_2 =r_1 :r_2、$
$同様に CD_1 :CD_3 =γ:CD_3 =r_1 :r_3$ となる。従って、$BD_2=\frac{r_2(s-b)}{r_1},CD_3=\frac{r_3(s-c)}{r_1} …£ $
さらに、図$4$のように、円$O_2$が$AB,AP$と接する点を
それぞれ$F_2,G_2$とし、円$O_3$が$AC,AP$と接する点
をそれぞれ$E_3, G_3$とする。
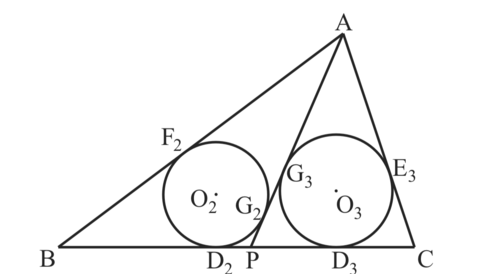図4
このとき$△ABP$の面積は、
$|△ABP|=\frac{r_2}{2}(AB+BP+PA)$
$=\frac{r_2}{2}(AB+BP+PG_3 +AG_3)$
$=\frac{r_2}{2}(AB+BP+PD_3 +AE_3)$
$=\frac{r_2}{2}(AB+BD_3 +AE3)$
$=\frac{r_2}{2}(AB+ BC−CD_3 +CA−CE_3)$
$=\frac{r_2}{2}(a+b+c−2CD_3)=\frac{r_2}{2}(s−CD_3)$
である。$|△APD|$についても同様。従って、
$△ABP = r_2(s − CD_3), △APC = r_3(s − BD_2) となる。$$ここで、式 £を代入すると、$
$△ABP=r_2s-\frac{r_2r_3(s-c)}{r_1},$
$△APC=r_3s-\frac{r_2r_3(s-b)}{r_1}$
$最後に△ABP+△APC=△ABC=\frac{1}{2}ahより、$
$(r_2+r_3)s-\frac{r_2r_3(2s-b-c)}{r_1}$$=\frac{1}{2}ah$
$(r_2+r_3)s-\frac{ar_2r_3}{r_1}$$=\frac{1}{2}ah$
$(r_2+r_3)r_1s-ar_2r_3-\frac{1}{2}ahr_1=0$
$ここでr_1s=\frac{1}{2}ahより、$
$h(r_2+r_3-r_1)-2r_2r_3=0$//
以上大意は『算法助術』より
次回、この補題の形を変えて使います。
投稿日：2021年1月2日
投稿者
投稿者
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
コメント
コメント