行列式と面積

はじめに

前回の記事 で，行列の固有値と固有ベクトルについて書きましたが，そのときにタイトルのことを思い出したので，それについてもまとめてみることにしました．なお，この記事では基本的に$2\times2$行列について考えることにします（高校数学でよくでてくるので）．

よく知られた事実

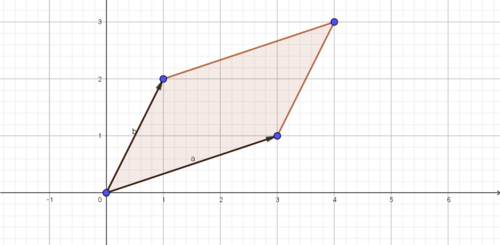vec1

この$ad-bc$が行列$ A = \left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right)$の行列式であり，$\det A$などともかく．これは，次の（これまたよく知られた事実）と一致している．

こちらの方が高校生にはなじみがあると思われる（おそらく教科書にも問題として掲載があることが多い）．この証明は三角形の面積を愚直に計算すればよい．

理由を考える

まず，行列と固有値について次が成り立っている（一般に$n$次でも成り立つ）ことを認めよう．

また，行列$A$の固有ベクトル$\vec{p}$とその固有値$\lambda$においては$A\vec{p} = \lambda \vec{p}$が成り立っていた．これは行列$A$を掛けるという線形変換においては固有ベクトルは回転されず，定数倍の伸び縮みしかしないということである．ここで$A$の$2$つの固有ベクトルを$\vec{p_1}$，$\vec{p_2}$と,その固有値$\lambda_1$，$\lambda_2$とすると，$\vec{p_1}$，$\vec{p_2}$で作られる四角形（平行四辺形）の面積は行列$A$による変換を考えると，次のようになっているということである．
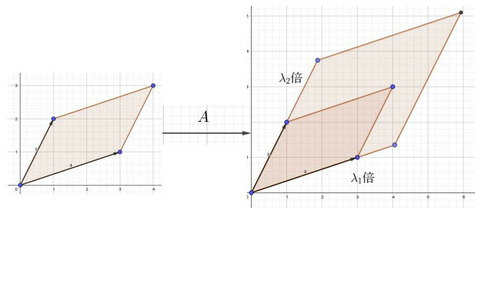線形変換
つまり，行列$A$による線形変換では$2$つの固有ベクトルが作る平行四辺形の面積は$2$つの固有値の積$\lambda_1\lambda_2$倍変化するということである．ここで，先に紹介した事実を用いれば$\lambda_1\lambda_2=\det{A}$であるから結局，面積は$\det A$倍される．
固有ベクトルではない$\vec{q_1}$，$\vec{q_2}$が作る平行四辺形の面積についても，$\vec{q_1}$，$\vec{q_2}$を$\vec{p_1}$，$\vec{p_2}$の線形結合で書き直すことができるので$\vec{q_1}$，$\vec{q_2}$から作られる平行四辺形の面積はやはり$\det A$倍される．

まとめ

つまり，$\vec{a}=(a,c),\ \vec{b} = (b,d)$によって作られる平行四辺形の面積は，$2$次元ベクトル空間の正規直交基底$e_1=\left( \begin{array}{c} 1 \\ 0\\ \end{array} \right) $，$e_1=\left( \begin{array}{c} 0 \\ 1\\ \end{array} \right) $により作られる平行四辺形の面積が$1$であり，$\vec{e_1}$，$\vec{e_2}$をいつでも$^1$行列$A$の固有ベクトルを用いて書き直すことができるので，その面積は固有値の積だけ拡大される．つまり$\det A$倍され，元の面積は$1$であったから結局，面積は$\det A = ad-bc$となる．

$^1$固有ベクトルが$2$つとれる場合はその$2$つの固有ベクトルは$1$次独立になる．