ファジィ理論とその応用

最近ファジィ制御について学ぶ機会がありました。ファジィという名前は前から聞いたことはあったのですが、どこか確率と同じようなもので今は学ぶ必要は無いんじゃないかと勘違いして遠ざけてしまっていました。しかし、ファジィを知るにつれてファジィ理論は確率論とはまた違った事象を数学的なモデルを通して捉えている理論なのだということが分かってきました。今回ファジィ制御について学んだことを忘れないように、数式とプログラムを添えながらまとめていきたいと思います。

ファジィ集合

ファジィ理論は主観的な曖昧さを扱うための枠組みです。例えば「身長が高い人の集合」や「年齢が若い人の集合」のような"集合"は定義が曖昧であるために_きちんと_定義することができません。しかし、身長168cmの人が「身長が高い人の集合」に属する度合いは $0.7$ というように集合に属するという概念を実数値を使って曖昧にしてやれば、その値の対応全体を使って「身長が高い人の集合」に近いような概念を定義することができそうです。

1965年、カリフォルニア大学のザデー教授[^1]は "Fuzzy Sets" という論文の中で、現在のファジィ理論の起源となるファジィ集合という概念を提唱しました。ファジィ集合は部分集合の考え方を拡張した概念になっていて、まず通常の集合論において集合$X$の部分集合$A$があったときに、以下のような特性関数$\chi_A$を定義することができます。

$$ \chi_A(x) = \begin{cases}1&x\in A\\0&x \notin A\end{cases} $$

逆に上記のような$X$を定義域とし$0, 1$の値を取る関数$\chi'$が与えられれば、それを使って部分集合$A$を定義することが可能です。

$$ A = \{x \ |\ x \in X, \chi'(x) = 1 \} $$

このように、部分集合と特性関数は密接に関連しています。
この特性関数が取る値の範囲を $\{0, 1\}$ の2値ではなく区間 $[0, 1]$に取るように拡張することを考えます。このように拡張した関数$\mu$を メンバーシップ関数 と呼び、各要素が考えている"集合"に属する度合いを与えると解釈します。そしてこのメンバーシップ関数が表している"集合"のことをファジィ集合と呼びます。

$$ \mu : X \rightarrow [0,1] $$

例えば「身長が高い人の集合」を改めて考えてみると、通常の集合（これをファジィ集合と対比してクリスプ集合と呼びます）では「身長が180cm以上の人の集合」のように定義する必要があり、その特性関数は下図のようになります。（※180cm以上の人が身長が高いというのはあくまで例えの話です。）

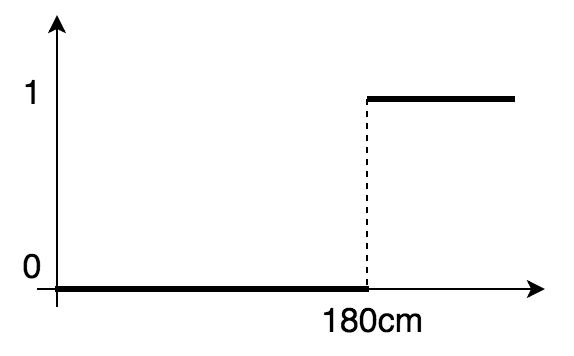
しかし、これだと179cmの人が身長が高くない人に分類されてしまいます。直感的には179cmの人はほとんど身長が高い人の集合に含まれると考えるのが普通でしょう。そこでファジィ集合を使うと以下のようなメンバーシップ関数を考えることができます。

179cmの人はメンバーシップ関数の値が1に近い値となりほとんど身長が高い人の集合に含まれることを表すことができました。

ファジィ理論と確率論の違い

ファジィ集合では曖昧な概念に$[0,1]$の値を割り当てましたが、同じように不確実性のある現象に$[0,1]$の値を割り当てる確率とはどのように違うのでしょうか。まず単純にメンバーシップ関数と確率測度を対比して考えると、メンバーシップ関数は各要素に対して値を割り当てるのに対して、確率測度は可測集合に対して値を割り当てます。この違いは特に無限個の要素を持つ集合を考えると顕著で、先程の身長が高い人の集合を例に取れば、メンバーシップ関数は具体的な身長の値に対してそれがファジィ集合に属する度合いを計算することができますが、確率測度は具体的な身長が一つ与えられてもその確率を計算することはできません（1点集合だと考えれば値はおそらく0です）。以下の例はより直感的に両者の違いが分かりやすく説明されています。

例えば，「あの人は若い」というときの「若い」という概念は，曖昧であるがこれはファジィ的な曖昧さであり，決して「若い」という概念がランダムであるとはいえない．「あの人はまあ半分くらい美人といえるだろう．」とはいえても「あの人が美人である確率は半分くらいだ．」とはいえない．つまり美人という曖昧な概念は，ファジィ性をもつのであり，ランダム性を持つのではないからだ．
出典: ファジィ集合と可能性と確率と

ファジィ集合論は「言葉の曖昧性」を扱い、確率論は「現象の蓋然性」を扱うと端的に表されるように[^2]、ファジィ集合論と確率論では数理的なモデル化を行う対象が違うというのが両者の根本的な違いになります[^3][^4]。メンバーシップ関数が$[0, 1]$の値を取ることが両者の紛らわしさの原因であるとすれば、ファジィ集合論が確率論と違うところとしては、ファジィ集合論の拡張としてメンバーシップ関数が取る値を$[0, 1]$から前順序集合や束に拡張した Lファジィ集合 という一般化が行われ研究されていることも特筆すべきでしょう。現代ではこのLファジィ集合が住むGoguen圏という圏も開発されて研究が進められているそうです。このようにファジィと確率は違う概念であるが故に、 ファジィ確率変数 のように曖昧性と不確実性を同時に含むデータを扱うための概念も考えることができます。

ファジィ集合の演算

ファジィ集合のアイデアである要素の属する属さないを2値ではなく連続的な値に置き換えるというのは非常にシンプルなものですが、単に部分集合を拡張したものであるだけでなく通常の集合に対するよく知られた演算もファジィ集合のものに拡張して定義することができます。以下で定義する概念はいずれもメンバーシップ関数を特性関数と読み替えれば通常の集合に対する概念に一致するので意識しながら読んでみてください。

二つのファジィ集合$A, B$が等しいということをそのメンバーシップ関数$\mu_A, \mu_B$が等しいことと定義します。

$$ A = B \iff \mu_A(x) = \mu_B(x), \forall x \in X $$

包含関係、例えばファジィ集合$A$がファジィ集合$B$に含まれているということをメンバーシップ関数の順序によって定義します。

$$ A \subset B \iff \mu_A(x) \leq \mu_B(x), \forall x \in X $$

ファジィ集合同士の共通集合$A \cap B$のメンバーシップ関数$\mu_{A \cap B}$は以下のように定義することができます。

$$ \mu_{A \cap B}(x) = {\rm min}(\mu_A(x), \mu_B(x)) $$

ファジィ集合同士の和集合$A \cup B$のメンバーシップ関数$\mu_{A \cup B}$は以下のように定義することができます。

$$ \mu_{A \cup B}(x) = {\rm max}(\mu_A(x), \mu_B(x)) $$

ファジィ集合$A$の補集合$A^c$のメンバーシップ関数$\mu_{A^c}$は以下のように定義することができます。

$$ \mu_{A^c} = 1 - \mu_A $$

このように定義してきた演算は例えば補集合の補集合が元の集合と一致したり

$$ (A^c)^c = A $$

ド・モルガンの法則を満たすことも分かります。

$$ \begin{matrix} (A \cup B)^c &=& A^c \cap B^c \\ (A \cap B)^c &=& A^c \cup B^c \\ \end{matrix} $$

ファジィ論理

実はファジィ集合論のメンバーシップ関数を集合への帰属度合いではなく、どれだけ真に近いかという多値論理として解釈することによりファジィ論理という論理体系を考えることができます。これによりファジィ論理では「彼は身長が高い」や「53万は高い戦闘力である」のような曖昧な命題も扱うことが可能になります。

ファジィ論理において論理積・論理和・否定として考えられる演算はまさにファジィ集合で定義した共通集合・和集合・補集合の演算に対応します。しかし通常の論理の拡張として定義されるこれらの演算は上で定義したものだけではなく他にも無数に存在します。例えば論理積として

$$ \mu_{A \times B}(x) = \mu_A(x) \cdot \mu_B(x) $$

論理和として

$$ \mu_{A + B}(x) = \mu_A(x) + \mu_B(x) - \mu_A(x) \cdot \mu_B(x) $$

と定義すると、これらも通常の論理演算を拡張したものになっており、それぞれ代数積・代数和と呼ばれています。こうした無数の演算の中でも t-norm (triangular norm) と呼ばれるクラスの演算は重要な研究対象になっているようです[^5]。t-normの定義は書きませんが、t-normを論理積、t-conormを論理和と考えることでド・モルガンの法則を満たす幅広い演算を考えることができます。例えば一見複雑に見える以下のような式もt-norm, t-conormの性質を満たしており、ファジィ論理の論理積・論理和として考えることができます。

$$ \begin{matrix} \mu_{A \times B}(x) &=& \frac{\mu_A(x) \cdot \mu_B(x)}{2 - (\mu_A(x) + \mu_B(x) - \mu_A(x) \cdot \mu_B(x))} \\ \mu_{A + B}(x) &=& \frac{\mu_A(x) + \mu_B(x)}{1 + \mu_A(x) \cdot \mu_B(x)} \end{matrix} $$

これらの演算はアインシュタイン積・アインシュタイン和と呼ばれているそうです[^6]。様々なt-normの作り方は Construction of t-norms というWikipediaにまとめられており眺めてるだけで楽しいと思います。

ファジィ論理における含意 $A \Rightarrow B$ ($A$ならば$B$)は以下のように定義されます。

$$ C \times A \leq B \iff C \leq A \Rightarrow B $$

すなわち論理積とファジィ集合としての包含関係について左辺のような関係式が成り立つとき、$C$を包含する$A \Rightarrow B$という命題が1対1に存在し、それを含意と定めます[^7]。含意となるファジィ集合は具体的に書き下すと以下のようになります。

$$ A \Rightarrow B = {\rm sup}\{C \ |\ C \times A \leq B \} $$

例えば論理積として共通集合の演算を採用すると含意は

$$ \mu_{A \Rightarrow B}(a, b) = \begin{cases}\mu_B(b)&\mu_A(a)>\mu_B(b)\\1&\mu_A(a)\leq\mu_B(b)\end{cases} $$

となり、また論理積として代数積を採用すると、

$$ \mu_{A \Rightarrow B}(a, b) = \begin{cases}\frac{\mu_B(b)}{\mu_A(a)}&\mu_A(a)>\mu_B(b)\\1&\mu_A(a)\leq\mu_B(b)\end{cases} $$

となります。これらの含意はそれぞれ標準ゲーデル含意とゴーグエン含意と呼ばれているようです[^8]。

含意の定義より、特に

$$ (A \Rightarrow B) \times A \leq B $$

が分かります。これはファジィ版の モーダスポネンス （AならばB。Aである。従ってBである）、すなわち論証と解釈することができ、ファジィ論理を使って推論を行う際の重要な概念となります。

ファジィ制御

ファジィ集合やファジィ論理を利用して制御モデルを構成するファジィ制御という分野があります。ファジィ制御では例えば自動車の運転を考えたときに「もし速度が遅ければアクセルを踏む」というような曖昧な表現が含まれたルールを並べて制御を行うことができます。またこういったルールが与えられたときに「もし速度がちょっと遅ければアクセルをちょっと踏む」というような振る舞いも導出することができます。このように人間の知識を素直に表現できることがファジィ制御の特徴です。

ファジィ制御は以下のような3つのステップで考えることができます。

ファジィ化

ファジィ化は外界から得られた入力をファジィ集合に変換するためのステップです。入力として特定の値が得られたのなら一点だけ1となるようなメンバーシップ関数を考えても良いですし ファジィ数 を使って表現することもできます。また、エアコンのように「やや強い風量」みたいな入力が与えられたら予め用意しておいたメンバーシップ関数を単純に割り当てるというのも良いでしょう。

ファジィ推論

ファジィ化によって入力のファジィ集合が与えられたら次はファジィ推論を行なっていきます。ファジィ推論では含意$A \Rightarrow B$を以下のようなIF-THENルールで表現することが多いようです。

$$ {\rm IF}\ \ X \ {\rm is} \ A\ \ {\rm THEN}\ \ Y \ {\rm is} \ B $$

$X, Y$は対象です。$X \ {\rm is} \ A$の部分を前件部、 $Y \ {\rm is} \ B$の部分を後件部といいます。例えば自動車の運転を考えると

$$ {\rm IF}\ \ 「速度」が「遅い」\ \ {\rm THEN}\ \ 「アクセル」を「踏む」 $$

$$ {\rm IF}\ \ 「速度」が「速い」\ \ {\rm THEN}\ \ 「アクセル」を「戻す」 $$

のようなイメージです。この例のようにファジィ推論は複数の推論規則を並べて使うことも可能です。

上述の推論規則が与えられたときに「速度」が「ちょっと遅い」から「アクセル」を「ちょっと踏む」を導出する過程を見てみましょう。

ファジィ推論を行う方法はたくさんありますが、今回はマムダニ法と呼ばれる方法を使います。手順としては

1. 前件部の命題と入力のmin（積）を取る
2. 1で作ったメンバーシップ関数の最大値を適合度とする
3. 適合度と後件部の命題のminを取り、計算された関数を推論結果のメンバーシップ関数とする
4. 1~3で得られた全てのファジィ集合のmax（和）を計算し全体の推論結果とする

という流れになります。

速度が「遅い」「ちょっと遅い」「普通」「ちょっと速い」「速い」を表すファジィ集合として以下のようなものを考えましょう。

重なって少し見えづらくなってしまっていますが5つのメンバーシップ関数があると考えてください。次にアクセルを「戻す」「そのまま」「踏む」を表すファジィ集合を考えてみます。

こちらも3つのファジィ集合とそれに付随するメンバーシップ関数があると考えてください。横軸はそれぞれ速度とアクセルの度合いの連続値を表しています。

今入力として「ちょっと遅い」を表すファジィ集合が与えられたとします。まずは1番目の

$$ {\rm IF}\ \ 「速度」が「遅い」\ \ {\rm THEN}\ \ 「アクセル」を「踏む」 $$

という推論規則を評価してみましょう。

マムダニ法に従って、「遅い」と「ちょっと遅い」のmin（積）を取り、その最大値を適合度とし、適合度と「アクセル」を「踏む」のminを取りメンバーシップ関数を計算した手順を以下の図で表しています。

推論結果として右図のメンバーシップ関数が得られています。

次に2番目の

$$ {\rm IF}\ \ 「速度」が「速い」\ \ {\rm THEN}\ \ 「アクセル」を「戻す」 $$

という推論規則を評価してみましょう。

最後にこれまでの評価によって得られたファジィ集合の和集合を取ります。

これで「ちょっと遅い」時のアクセルに対する操作を表すファジィ集合が得られました。「遅い」時に導かれる「踏む」一辺倒のファジィ集合ではなく、ある程度「戻す」も考慮されたファジィ集合になっているのがわかるかと思います。

非ファジィ化

ファジィ推論で得られたファジィ集合から一つの値を取り出す操作を非ファジィ化と呼びます。今回の例では実際にアクセルに対してどのようなアクションを行えばいいかを計算するために、重心法を利用します。重心法はその名前の通りファジィ集合の"重心"を求める方法で、以下のような計算を行います。

$$ output = \frac{\int y \cdot \mu_B(y) dy}{\int \mu_B(y) dy} $$

$c$が求める値で$y$はアクセルに対するアクション、$\mu_B$はファジィ推論によって得られたメンバーシップ関数です。今回の例で計算すると下図のような値が得られると思います。「ちょっと遅い」場合に「ちょっと踏む」という結果がちゃんと得られましたね。今回使ったマムダニ法はその手順からmin-max重心法とも呼ばれています。

こうしたファジィ制御は実際に様々な場面で応用されており、例えば1990年にファジー洗濯機という家電製品が販売され大ヒットしたという歴史もあるようです[^9]。家電のみならず工場や鉄道でも使われており、応用事例に関しては日本知能情報ファジィ学会が公開している ファジィ応用事例データベース から見つけることができます。

[^1]: Lotfi A. Zadeh 教授。2017年9月6日にご逝去されたそうです。
[^2]: 追悼 Zadeh（ザデー）先生を偲んで
[^3]: しかし確率論の主観確率という概念を使えばファジィ集合論が扱おうとしている概念も扱えるのではないかと思われるかもしれません。これに関しては "不確定性表現の基盤としてのファジィ理論" という文章に主観確率とファジィ理論の違いが書かれているので参照してみてください。
[^4]: ファジィ集合論から確率論の枠組みを考える 可能性理論 というのもあるそうです。
[^5]: ファジィ論理のほとんど全て（16） – ファジィ論理はどこに紛れたか –
[^6]: H.-J. Zimmermann, "Fuzzy set theory"
[^7]: これは ガロア接続 の形になっていて、論理積の 随伴 として含意を定めるという定義になっています。
[^8]: T-norm # Residua of prominent left-continuous t-norms
[^9]: あいまいさの効用 -ファジィ理論とその周辺-