元日算額解説〜弐の巻・完〜

545

第2章です。今回は前回証明した補題を変形して用います。
現在解いている問題↓
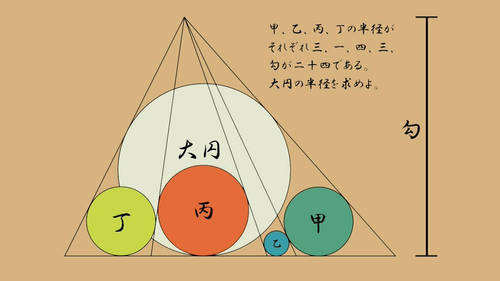
問題

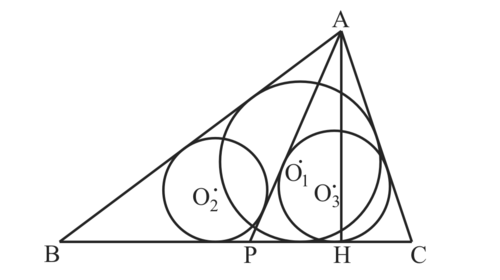
$図 1$ のように $3 円 O_{1}, O_{2}, O_{3}$ はそれぞれ $△ A B C, △ A B P, △ A P C$ の内接円とする。 $また、頂点 A から辺 B C$ に下ろした垂線の $足を H とする。$ $このとき、円 O_{1}, O_{2}, O_{3}$ の半径を $それぞれ r_{1}, r_{2}, r_{3} とし、$ $A H = h とするとき、$

$h (r_{2} + r_{3} - r_{1}) - 2 r_{2} r_{3} = 0$
である。
画像1 図1

証明を見たい方は〜壱の巻〜をご覧ください。
では始めます。

まず最初に(ここが一番大事ですが)
$h (r_{2} + r_{3} - r_{1}) - 2 r_{2} r_{3} = 0$
を
$(1 - \frac{2 r_{1}}{h}) = (1 - \frac{2 r_{2}}{h}) (1 - \frac{2 r_{3}}{h}) \dots €$
に変形します。
展開すれば二つの式が等しいことがわかります。
何と美しいことか。
野暮かもしれませんが解説しましょう。
これのどこが嬉しいかというと、

① $r_{1}, r_{2}, r_{3}$ の形が1つに揃う
②左辺と右辺で明確な半径の区別がされる
③シンプルで汎用性が高い
といったところでしょうか。

ここまでくればもう一息です。
(問題再掲)
問題

問題図改図(改)
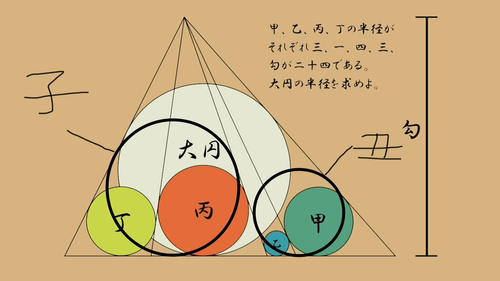
ここで簡単のため、上図における(大円、子、丑、甲、乙、丙、丁)の半径をそれぞれ(大、子、丑、甲、乙、丙、丁)の文字で置くこととします。
$€$ より上図において、
$(1 - \frac{2 大}{勾}) = (1 - \frac{2 子}{勾}) (1 - \frac{2 丑}{勾})$ ,
$(1 - \frac{2 丑}{勾}) = (1 - \frac{2 甲}{勾}) (1 - \frac{2 乙}{勾})$
$(1 - \frac{2 子}{勾}) = (1 - \frac{2 丙}{勾}) (1 - \frac{2 丁}{勾})$ が成り立ちます。
これらの式を合わせて、
$(1 - \frac{2 大}{勾}) = (1 - \frac{2 甲}{勾}) (1 - \frac{2 乙}{勾}) (1 - \frac{2 丙}{勾}) (1 - \frac{2 丁}{勾})$ を得ます。
最後に甲=3,乙=1,丙=4,丁=3,勾=24を代入して解くことで、
大= $\frac{63}{8}$ 、
よって求める大円の半径は $\frac{63}{8}$ です。