受入保留アルゴリズムのグループ耐戦略性
はじめに
本記事では,受入保留アルゴリズム(deferred acceptance algorithm;DAアルゴリズム)のグループ耐戦略性を証明します.
(必要に応じて導入部分を追記します.)
参考
本記事の証明は以下の教科書を参考にしています.
前提知識
本記事では,以下を前提知識とします.
- マッチングの定義
- 選好の定義
- 安定マッチングの定義
- DAアルゴリズム
記号
- 男性の集合$M = \{ m, ... \}$
- 女性の集合$W = \{ w, ... \}$
- $|M| = |W| = n$
- マッチング$x = \{ (m, w), ... \}$
- 男性$m$の選好$\succsim_m$(女性集合の全順序)
- 女性$w$の選好$\succsim_w$(男性集合の全順序)
- 全員の選好の集合$\succsim = (\succsim_m, ..., \succsim_w, ...)$
定理
任意の真の選好を$\succsim$,任意の男性グループを$M'$,男性グループの選好を任意に変更した選好を$\succsim'$とする.また,選好$\succsim$でのDAマッチングを$x_\succsim$,選好$\succsim'$でのDAマッチングを$x_{\succsim'}$とする.マッチングアルゴリズムがグループ耐戦略性を持つとき,男性$m \in M'$がマッチング$x_\succsim$よりもマッチング$x_{\succsim'}$で良い女性とペアになるような男性グループ$M'$は存在しない.
DAアルゴリズムはグループ耐戦略性を満たす.
定理1を証明する上でカギになるのが以下の補題2です.
任意の選好を$\succsim$,任意のマッチングを$x$とする.また,選好$\succsim$のDAマッチングを$x_\succsim$,$x(m) \succ_m x_\succsim(m)$である男性$m$の集合を$\tilde{M}$とする.男性集合$\tilde{M}$が非空のとき,以下を満たすペア$(m, w)$が存在する.
- $m \not \in \tilde{M}$
- $x(w) \in \tilde{M}$
- マッチング$x$と選好$\succsim$において不安定
DAマッチングの最適性より,DAマッチングよりも良い女性とペアになる男性がいるマッチングは不安定になることが分かりますが,補題2では,不安定なペアを具体的に特徴付けしています.耐戦略性の証明に使えるだけではなく,補題自体の内容がとても重要だと思います.
証明
補題の条件を満たすペアを具体的に構成することで証明する.
以下の記号を使う.
- 男性$m \in \tilde{M}$
- 男性$m$のマッチング$x$での相手の女性$w = x(m)$($m = x(w)$)
- 女性$w$のマッチング$x_\succsim$での相手の男性$m' = x_\succsim(w)$($w = x_\succsim(m')$)
選好を整理する.$m \in \tilde{M}$より,男性$m$の好みは$w \succ_m x_\succsim(m)$である.また,ペア$(m', w)$はマッチング$x_\succsim$と選好$\succsim$において安定であるため,女性$w$の好みは$m' \succ_w m ... (1)$である.
男性$m'$が男性集合$\tilde{M}$に含まれるかどうかで場合分けする.
- $m' \not \in \tilde{M}$となる男性$m'$がいる場合
概要を図1に示す.
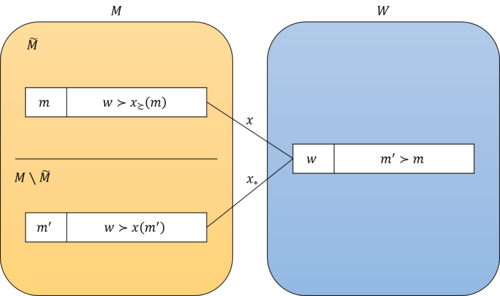 図1
図1
ペア$(m', w)$が補題の条件を満たすことを示す.
仮定より,$m' \not \in \tilde{M}, x(w) \in \tilde{M}$である.
マッチング$x$と選好$\succsim$において,ペア$(m', w)$が不安定であることを示す.$m' \not \in \tilde{M}$より,男性$m'$の好みは$w \succ_{m'} x(m') ... (2)$である.ここで,$w \neq x(m')$なのは,$w = x(m) \neq x(m')$だからである.式(1)(2)より,マッチング$x$と選好$\succsim$において,ペア$(m', w)$は不安定である.
- 任意の男性$m'$が$m' \in \tilde{M}$の場合
概要を図2に示す.
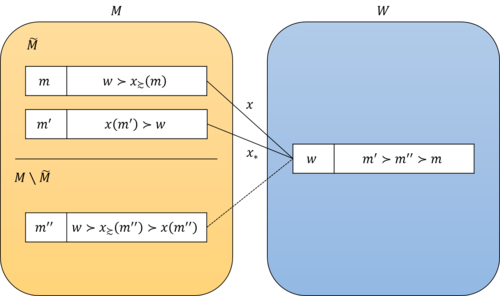 図2
図2
選好$\succsim$のDAアルゴリズムで男性集合$\tilde{M}$の中で最後に告白する男性が$m'$となるように,男性$m$を選択する.男性$m'$は最後の告白で最終的な相手である女性$w$に告白する.このとき,女性$w$に振られる男性を$m''$とする.
ペア$(m'', w)$が補題の条件を満たすペアであることを示す.
男性$m'$が女性$w$に告白する時点で,女性$w$に仮の相手の男性$m''$が存在することを示す.式(1)より,男性$m$は女性$x_\succsim(m)$よりも先に女性$w$に告白する.また,男性グループ$\tilde{M}$の中で最後に告白するのが男性$m'$であることから,男性$m$は男性$m'$よりも先に女性$w$に告白する.したがって,男性$m'$が女性$w$に告白する時点で,女性$w$に仮の相手の男性$m''$が存在する.ただし,男性$m$が男性$m''$であるとは限らないことに注意する.
選好を整理する.$m' \in \tilde{M}$より,男性$m'$の好みは$x(m') \succ_{m'} w$である.また,男性$m''$は女性$x_\succsim(m'')$とペアになる前に女性$w$に振られることと,$m'' \not \in \tilde{M}$より,男性$m''$の好みは$w \succ_{m''} x_\succ(m'') \succ_{m''} x(m'') ... (3)$である.さらに,男性$m'$の前に男性$m, m''$が女性$w$に告白することと,男性$m'$が女性$w$に告白する時点で女性$w$の仮のペアの男性が$m''$であることから,男性$w$の好みは$m' \succ_w m'' \succ_w m ... (4)$である.
式(3)(4)より,マッチング$x$と選好$\succsim$においてペア$(m'', w)$は不安定である.
男性$m''$が男性集合$\tilde{M}$に含まれないことを示す.男性$m''$が男性集合$\tilde{M}$に含まれると仮定する.式(4)より,男性$m'$が女性$w$に告白したとき,男性$m''$は女性$w$から振られる.そのため,男性$m'$は次のステップ以降にも告白する.これは,男性$m'$が男性集合$\tilde{M}$の中で最後に告白することに矛盾する.したがって,男性$m''$は男性集合$\tilde{M}$に含まれない.
前述の説明より$m'' \not \in \tilde{M}$,仮定より$x(w) \in \tilde{M}$である.□
定理の反例となる男性グループ$M'$と選好$\succsim'$があると仮定する.男性グループ$M'$以外の選好は変更していないことに注意する.また,マッチング$x_{\succsim'}$は選好$\succsim'$において安定であることを確認しておく.
選好$\succsim$とマッチング$x_{\succsim'}$に補題2を適用する.このとき,男性集合$\tilde{M}$は$M' \subseteq \tilde{M}$である.また,$m \not \in \tilde{M}$であり,マッチング$x_{\succsim'}$と選好$\succsim$において不安定なペア$(m, w)$が存在する.$m \not \in \tilde{M}$より,男性$m$の選好は$\succsim_m = \succsim'_m$であるから,マッチング$x_{\succsim'}$と選好$\succsim'$においてもペア$(m, w)$は不安定である.これは,マッチング$x_{\succsim'}$が選好$\succsim'$において安定であることに矛盾する.□
おわりに
本記事では,DAアルゴリズムのグループ耐戦略性を証明しました.グループ耐戦略性は個人耐戦略性を拡張した性質です.個人耐戦略性については こちら で扱いました.ただ,式で証明(参考1)は追えても,深く理解できた気がしていませんでした.そこで,別証明も見てみようと思い,参考2の証明を読み,補題2を通した証明に出会いました.補題2は,背理法を用いない構成的な方法で証明しているため理解しやすく,さらに,その内容自体も重要であるため,とても感銘を受けました.今後も耐戦略性に関する理解を深めていきたいです.