解説したい問題の解説

定積分

問１

解答
$$ \begin{eqnarray} I&=&\int_0^\frac{π}{4}\frac{x}{\sin2x+2\cos^2x}dx\\ &=&\int_0^\frac{π}{4}\frac{x}{\sin2x+\cos2x+1}dx\\ \end{eqnarray} \\ t=\frac{π}{4}-xと置換すると $$
$$ \begin{eqnarray} I&=&\int_\frac{π}{4}^0\frac{\frac{π}{4}-t}{\sin2\left(\frac{π}{4}-t\right)+\cos\left(\frac{π}{4}-t\right)+1}\left(-dt\right)\\ &=&\int_0^\frac{π}{4}\frac{\frac{π}{4}-x}{\sin2x+\cos2x+1}dx\\ \end{eqnarray}\\ したがって、\\ $$
$$ \begin{eqnarray} I&=&\frac{1}{2}\left(I+I\right)\\ &=&\frac{1}{2}\left(\int_0^\frac{π}{4}\frac{x}{\sin2x+\cos2x+1}dx+\int_0^\frac{π}{4}\frac{\frac{π}{4}-x}{\sin2x+\cos2x+1}dx\right)\\ &=&\frac{π}{8}\int_0^\frac{π}{4}\frac{1}{\sin2x+\cos2x+1}dx\\ さらに、y=\tan xと置換すると\\ dx=\frac{1}{1+y^2}dy\\ \sin2x=\frac{2y}{1+y^2}\\ \cos2x=\frac{1-y^2}{1+y^2}\\ であるため、\\ I&=&\frac{π}{8}\int_0^1\frac{1}{\frac{2y}{1+y^2}+\frac{1-y^2}{1+y^2}+1}\frac{1}{1+y^2}dy\\ &=&\frac{π}{8}\int_0^1\frac{1}{2y+1-y^2+1+y^2}dy\\ &=&\frac{π}{16}\int_0^1\frac{1}{1+y}dy\\ &=&\frac{π}{16}\Big[\log|1+y|\Bigr]^1_0\\ &=&\frac{π}{16}\log2 \end{eqnarray} $$

問２

解答
$$ 分子・分母を\cos^2xで割る(\cos x\neq0)。\\ \begin{eqnarray} I&=&\int_0^\frac{π}{4}\frac{1}{1+2\sin^2x}dx\\ &=&\int_0^\frac{π}{4}\frac{\frac{1}{\cos^2x}}{\frac{1}{\cos^2x}+2\frac{\sin^2x}{\cos^2x}}dx\\ &=&\int_0^\frac{π}{4}\frac{1}{1+\tan x}・\frac{1}{\cos^2x}dx\\ \end{eqnarray} ここで、\sqrt{3}\tan x=\tan y\left(-\frac{π}{2}< y<\frac{π}{2}\right)とすると、x|0→\frac{π}{4}のときy|0→\frac{π}{3}であり、\\ \frac{dx}{\cos^2x}=\frac{dy}{\sqrt{3}\cos^2y}\\ であるから、 $$
$$ \begin{eqnarray} I&=&\int_0^\frac{π}{3}\frac{1}{1+\tan^2y}・\frac{1}{\sqrt{3}\cos^2y}dy\\ &=&\frac{\sqrt{3}}{3}\int_0^\frac{π}{3}dy\\ &=&\frac{\sqrt{3}}{3}\Big[y\Bigr]^\frac{π}{3}_0\\ &=&\frac{\sqrt{3}}{9}π \end{eqnarray} $$

問３

解答
$$ I=\int_o^\pi \frac{1}{1+2\sin^2x}dx=\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2x}dx+\int_\frac{\pi}{2}^\pi \frac{1}{1+2\sin^2x}dx\\ 第２項について、t=\pi-xと置換すると、\\ \int_\frac{\pi}{2}^\pi\frac{1}{1+2\sin^2x}dx=\int_\frac{\pi}{2}^0\frac{1}{1+2\sin^2(\pi-t)}(-dt)=\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2t}dt\\ \therefore I=2\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2x}dx\\ ここで、y=\tan\frac{x}{2}と置換すると、\\ dx=\frac{2}{1+y^2}dy\\ \sin x=\frac{2y}{1+y^2}\\ となるから、\\ \begin{eqnarray} \frac{1}{2}I&=&\int_0^1\frac{1}{1+2\left(\frac{2y}{1+y^2}\right)^2}・\frac{2}{1+y^2}dy\\ &=&\int_0^1\frac{2y^2+2}{y^4+10y^2+1}\\ &=&\int_0^1\frac{2y^2+2}{(y^2+5+2\sqrt{6})(y^2+5-2\sqrt{6})}dy \end{eqnarray} $$
$$ ここで、被積分関数について、\\ \frac{2y^2+2}{(y^2+5+2\sqrt{6})(y^2+5-2\sqrt{6})}=\frac{\sqrt3}{3}\left(\frac{\sqrt{3}+\sqrt{2}}{y^2+5+2\sqrt{6}}+\frac{\sqrt{3}-\sqrt{2}}{y^2+5-2\sqrt{6}}\right)\\ と部分分数分解される。\\ 第１項の積分について、(\sqrt{3}+\sqrt{2})^2=5+2\sqrt{6}であることを踏まえてy=(\sqrt{3}+\sqrt{2})\tan s\left(-\frac{\pi}{2}< s<\frac{\pi}{2}\right)と置換すると、\\ \begin{eqnarray} \int_0^1\frac{\sqrt{3}+\sqrt{2}}{y^2+5+2\sqrt{6}}dt&=&\int_0^\alpha\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}+\sqrt{2})^2(\tan^2s+1)}・\frac{\sqrt{3}+\sqrt{2}}{\cos^2s}ds\\ &=&\int_0^\alpha ds\\ &=&\alpha\\ \end{eqnarray} $$
$$ ただし、\alphaは\tan\alpha=\frac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}(0<\alpha<\frac{\pi}{2})を満たす弧度である。\\ 同様に、第２項の積分についても、y=(\sqrt{3}-\sqrt{2})\tan u(-\frac{\pi}{2}< u<\frac{\pi}{2})と置換すると\\ \int_0^1\frac{\sqrt{3}-\sqrt{2}}{y^2+5-2\sqrt{6}}dy=\int_0^\beta du=\beta\\ ただし、\betaは\tan\beta=\frac{1}{\sqrt{3}-\sqrt{2}}=\sqrt{3}+\sqrt{2}を満たす弧度である。\\ ここで、\\ \tan\alpha\tan\beta=(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})=1(...*)である。\\ また、加法定理から、\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}であり、(*)と\alpha,\beta共に鋭角から\\ \begin{eqnarray} \alpha+\beta=\frac{\pi}{2}\\ \therefore I&=&\frac{2\sqrt{3}}{3}\int_0^1\left(\frac{\sqrt{3}+\sqrt{2}}{y^2+5+2\sqrt{6}}+\frac{\sqrt{3}-\sqrt{2}}{y^2+5-2\sqrt{6}}\right)dy\\ &=&\frac{2\sqrt{3}}{3}(\alpha+\beta)\\ &=&\frac{\sqrt{3}}{3} \end{eqnarray} $$

解答
$$ I=\int_0^\pi\frac{1}{1+2\sin^2x}dx \\r=\sqrt{\frac{1}{1+2\sin^2θ}}\\ という極方程式を考える。これを直交座標における方程式に直すと、\\ r^2+2r^2\sin^2θ=1\\ \left(x^2+y^2\right)+2y^2=1\\ x^2+3y^2=1\\ これは、原点を中心とした楕円を表す。\\ また、\\ \frac{1}{2}I=\frac{1}{2}\int_0^\pi r^2dθ\\ について、その値が意味するものは、x^2+3y^2\leqq0かつy\geqq0が示す領域の面積であるため、\\ \begin{eqnarray} \frac{1}{2}I&=&1・\frac{\sqrt{3}}{3}・\pi \times \frac{1}{2}\\ &=&\frac{\sqrt{3}}{6}\\ \\ \therefore \quad\quad\int_0^\pi \frac{1}{1+\sin^2x}dx=\frac{\sqrt{3}}{3} \end{eqnarray} $$

問４

解法
$$ I=\int_0^{\pi} \frac{1}{3+\sin^22x}dx=\int_0^\frac{\pi}{2}\frac{1}{3+\sin^22x}dx+\int_\frac{\pi}{2}^\pi\frac{1}{3+\sin^22x}\\ 第２項について、x=\pi-tと置換すると、\\ \int_\frac{\pi}{2}^\pi\frac{1}{3+\sin^22x}dx=\int_\frac{\pi}{2}^0\frac{1}{3+\sin^2(\pi-t)}(-dt)=\int_0^\frac{\pi}{2}\frac{1}{3+\sin^22t}dt\\ すなわち、\\ \begin{eqnarray} \int_o^\pi\frac{1}{3+\sin^22x}dx&=&2\int_0^\frac{\pi}{2}\frac{1}{3+\sin^22x}dx\\ &=&2\int_0^\frac{\pi}{2}\frac{1}{3+4\sin^2x\cos^2x}dx\\ &=&\frac{1}{2}\int_0^\frac{\pi}{2}\frac{(1+2\cos^2x)+(1+2\sin^2x)}{(1+2\sin^2x)(1+2\cos^2x)}dx\\ &=&\frac{1}{2}\left(\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2x}dx+\int_0^\frac{pi}{2}\frac{1}{1+2\cos^2x}dx\right)\\ \end{eqnarray} $$
$$ この第２項について、x=\frac{\pi}{2}-yと置換すると、\\ \int_0^\frac{\pi}{2}\frac{1}{1+2\cos^2x}dx=\int_\frac{\pi}{2}^0\frac{1}{1+2\cos^2\left(\frac{\pi}{2}-y\right)}(-dy)=\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2y}dy\\ したがって、問３結果と合わせて、\\ \int_0^\pi\frac{1}{3+\sin^22x}dx=\int_0^\frac{\pi}{2}\frac{1}{1+2\sin^2x}dx=\frac{\sqrt{3}}{6}\pi $$

問５

解答
$$ r=\frac{3}{2+\sin θ}\\ という極方程式を考える。これを直交座標における方程式に直すと・\\ 2r＝3-r\sin θ\\ 2\sqrt{x^2+y^2}=3-y\\ 4(x^2+y^2)=9-6y+y^2\\ 4x^2+3(y+1)^2=12\\ \frac{x^2}{3}+\frac{(y+1)^2}{4}=1\\ $$

zu
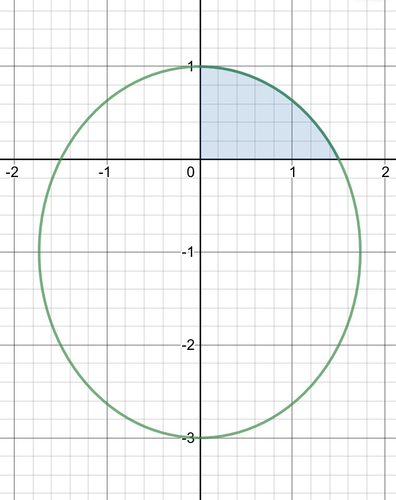
$$ \\ これは、点(0,-1)を中心とする上の楕円を表す。そして、\\ \frac{1}{2}I=\frac{1}{2}\int_0^\frac{\pi}{2}r^2dθ\\ について、その値が表すものは、\frac{x^2}{3}+\frac{(y+1)^2}{4}<0かつx\geqq0かつy\geqq0の示す領域の面積である。\\ x\geqq0の範囲において、\\ x=\frac{1}{2}\sqrt{12-3(y+1)^2}\\ であるから、上述の面積は、\\ \int_0^1xdy=\frac{1}{2}\int_o^1\sqrt{12-3(y+1)^2}dy\\ y+1=2\sin t\left(-\frac{\pi}{2}< t>\frac{\pi}{2}\right)と置換すると、y|0→1の時、t|\frac{\pi}{6}→\frac{\pi}{2}となるので、\\ $$
$$ \begin{eqnarray} \frac{1}{2}I&=&\frac{1}{2}\int_\frac{\pi}{6}^\frac{\pi}{2}\sqrt{12(1-\sin^2t)}・2\cos t dt\\ &=&2\sqrt{3}\int_\frac{\pi}{6}^\frac{\pi}{2}\cos^2t dt\\ &=&\sqrt{3}\int_\frac{\pi}{6}^\frac{\pi}{2}(1+2\cos2t)dt\\ &=&\sqrt{3}\Big[t+\frac{1}{2}\sin2t\Big]^\frac{\pi}{2}_\frac{\pi}{6}\\ &=&\frac{\sqrt{3}}{3}\pi-\frac{3}{4}\\ したがって、\\ \int_0^\frac{\pi}{2}\left(\frac{3}{2+\sin x}\right)^2dx=\frac{2\sqrt{3}}{3}-\frac{3}{2} \end{eqnarray} $$

問６

解答
$$ I=\int_0^\frac{\pi}{4}\sqrt{\tan x}dx\\ \sqrt{\tan x}=tと置換すると、\\ dx=\frac{2t}{1+t^4}となるから、\\ \begin{eqnarray} I&=&\int_0^1 t・\frac{2t}{1+t^4}dt\\ &=&\int_0^1\frac{2t^2}{1+t^4}dt\\ &=&\int_0^1\frac{2t^2}{(t^2+\sqrt{2}t+1)(t^2-\sqrt{2}+1)}dt\\ \end{eqnarray} $$
$$ この被積分関数を、\\ \frac{2t^2}{(t^2+\sqrt{2}t+1)(t^2-\sqrt{2}t+1)}=\frac{1}{\sqrt{2}}\left(\frac{t}{t^2-\sqrt{2}t+1}-\frac{t}{t^2+\sqrt{2}t+1}\right)\\ と部分分数分解し、各項の定積分をそれそれ\\ I_1=\int_0^1\frac{t}{t^2-\sqrt{2}t+1} dt\\ I_2=\int_0^1\frac{t}{t^2+\sqrt{2}t+1}dt\\ と置く。\\ I_1について、\\ I_1=\frac{1}{2}\int_0^1\frac{(t^2-\sqrt{2}t+1)'+\sqrt{2}}{t^2-\sqrt{2}t+1}dt=\frac{1}{2}\int_0^1\frac{(t^2-\sqrt{2}t+1)'}{t^2-\sqrt{2}t+1}dt+\frac{\sqrt{2}}{2}\int_0^1\frac{1}{t^2-\sqrt{2}t+1}dx\\ と変形すると、第１項は\\ \frac{1}{2}\int_0^1\frac{2t-\sqrt{2}}{t^2-\sqrt{2}t+1}dt=\frac{1}{2}\Big[\log|t^2-\sqrt{2}t+1\Big]^1_0=\frac{1}{2}\log(2-\sqrt{2})\\ 第２項は\\ \frac{\sqrt{2}}{2}\int_0^1\frac{1}{t^2-\sqrt{2}t+1}dt=\sqrt{2}\int_0^1\frac{1}{(\sqrt{2}t-1)^2+1}\\ \sqrt{2}-1=\tan u \left(-\frac{\pi}{2}< u<\frac{\pi}{2}\right)と置換すると、\\ \begin{eqnarray} \sqrt{2}\int_0^1\frac{1}{(\sqrt{2}t-1)^2+1}dx&=&\sqrt{2}\int_{-\frac{\pi}{4}}^\alpha\frac{1}{\tan^2u+1}・\frac{1}{\sqrt{2}\cos^2u}du\\ &=&\int_{-\frac{\pi}{4}}^\alpha du\\ &=&\alpha+\frac{\pi}{4}\\ ただし、\alphaは\tan\alpha=\sqrt{2}-1\left(0<\alpha<\frac{\pi}{2}\right)を満たす弧度である。\\ \end{eqnarray} $$
$$ I_2についても同様に、\\ I_2=\frac{1}{2}\int_0^1\frac{(t^2+\sqrt{2}t+1)'}{t^2+\sqrt{2}t+1}dt-\frac{\sqrt{2}}{2}\int_0^1\frac{1}{t^2+\sqrt{2}t+1}dt\\ と変形すると、第１項は\\ \frac{1}{2}\int_0^1\frac{2t+\sqrt{2}}{t^2+\sqrt{2}t+1}dt=\frac{1}{2}\Big[\log|t^2+\sqrt{2}t+1|\Big]^1_0=\frac{1}{2}\log(2+\sqrt{2})\\ 第２項は\\ \frac{\sqrt{2}}{2}\int_0^1\frac{1}{t^2+\sqrt{2}t+1}dt=\sqrt{2}\int_0^1\frac{1}{(\sqrt{2}t+1)^2+1}dt\\ \sqrt{2}t+1=\tan u\left(-\frac{1}{2}< u<\frac{1}{2}\right)と置換をすると、\\ \begin{eqnarray} \sqrt{2}\int_0^1\frac{1}{(\sqrt{2}+1)^2}dt&=&\sqrt{2}\int_\frac{\pi}{4}^\beta\frac{1}{\tan^2u+1}・\frac{1}{\sqrt{2}\cos^2u}du\\ &=&\int_\frac{\pi}{4}^\beta du\\ &=&\beta-\frac{\pi}{4}\\ \end{eqnarray} $$
$$ ただし、\betaは\tan\beta=\sqrt{2}+1\left(0<\beta<\frac{\pi}{2}\right)を満たす弧度である。\\ 以上より、\\ \begin{eqnarray} I&=&\frac{1}{\sqrt{2}}(I_1-I_2)\\ &=&\frac{1}{\sqrt{2}}\left\{\left(\frac{1}{2}\log(2-\sqrt{2})+\alpha+\frac{\pi}{4}\right)-\left(\frac{1}{2}\log(2+\sqrt{2})-/beta+\frac{\pi}{4}\right)\right\}\\ &=&\frac{1}{\sqrt{2}}\left(\frac{1}{2}\log(3-2\sqrt{2})+\alpha+\beta\right)\\ &=&\frac{1}{\sqrt{2}}\left(\log(\sqrt{2}-1)+\alpha+\beta\right)\\ \end{eqnarray} $$
$$ ここで、\\ \tan\alpha\tan\beta=(\sqrt{2}-1)(\sqrt{2}+1)=1\\ かつ\alpha,\betaともに鋭角であるため、問３と同様に、\\ \alpha+\beta=\frac{\pi}{2}\\ よって、\\ \int_0^\frac{\pi}{4}\sqrt{\tan x}dx=\frac{1}{\sqrt{2}}\left\{\log(\sqrt{2}-1)+\frac{\pi}{2}\right\} $$

問７

解答
$$ I=\lim_{n\to\infty}n\left(\log n\right)^2\left\{\sin\left(\frac{1}{\log n} \right) - \sin\left( \frac{1}{\log(n+1)}\right)\right\} \\ 平均値の定理より\\ \frac{\sin\left(\frac{1}{\log n}\right)-\sin\left(\frac{1}{\log(n+1)}\right)}{\frac{1}{\log n}-\frac{1}{\log (n+1)}}=(\sin c)'\left(\frac{1}{\log(n+1)}\leqq c\leqq \frac{1}{\log n}\right) \\すなわち\\ \sin\left(\frac{1}{\log n}\right)-\sin\left(\frac{1}{\log(n+1)}\right)=\left(\frac{1}{\log n}-\frac{1}{\log(n+1)}\right)(\sin c)'\left(\frac{1}{\log(n+1)} \leqq c \leqq \frac{1}{\log n}\right)\\ をとなるようなcが存在する。よって\\ \begin{eqnarray} I&=&\lim_{n\to\infty}n(\log n)^2\left(\frac{1}{\log n}-\frac{1}{\log(n+1)}\right)(\sin c)'\\ &=&\lim_{n\to\infty}n(\log n)^2\left(\frac{\log(n+1)-\log n}{\log n・\log(n+1)} \right)(\sin c)'\\ &=&\lim_{n\to\infty}n \log n \frac{\log\left(1+\frac{1}{n}\right)}{\log(n+1)}(\sin c)'\\ &=&\lim_{n\to\infty} \log\left(1+\frac{1}{n}\right)^n \frac{\log n}{\log (n+1)}(\sin c)' \end{eqnarray} $$
$$ ここで、\\ \lim_{n\to\infty}\log\left(1+\frac{1}{n}\right)^n=\lim_{n\to\infty}\log e=1...①\\ \begin{eqnarray} \frac{\log n}{\log(n+1)}&=&\frac{\log n}{\log n\left(1+ \frac{1}{n}\right)} &=&\frac{\log n}{\log n +\log\left(1+\frac{1}{n}\right)}\\ &=&\frac{1}{1+\frac{\log\left(1+\frac{1}{n}\right)}{\log n}}\\ \end{eqnarray} $$
$$ ここで、\lim_{n\to\infty}\frac{log\left(1+\frac{1}{n}\right)}{\log n}=0であるため、\\ \lim_{n\to\infty}\frac{\log n}{\log(n+1)}=1...②\\ (\sin c)'=\cos c であり、\\ {n\to\infty}と\frac{1}{\log(n+1)}\leqq c \leqq \frac{1}{\log n}から、はさみうちの原理により\\ c=0\\すなわち(\sin c)'=1...③ $$
$$ 以上より、\\ I=\lim_{n\to\infty}1×1×1=1 $$