JMO2021予選 解答解説 (1~4)
本番でやらかしてしまったnoyarulerによる禊解説です。ご査収ください。
1.互いに素な正の整数 $m,n$ が $m+n=90$ を満たすとき, 積 $mn$ としてありうる最大の値を求めよ.
答え $2021$
一般性を失わず $m\le n$ とする。
$mn=m(90-m)=-m^2+90m=-(m-45)^2+2025$
より、これは $m\le 45$ の範囲で単調増加である。
従って、$x\le y\le 45$ ならば $-(x-45)^2+2025\le -(y-45)^2+2025$ が言える。$m=43,n=47$ のときに $m,n$ が互いに素であることが分かり、$m=45,44$ のときは $m,n$ は互いに素でないことから、$mn$ としてありうる最大の値は $43\times 47 = 2021$ と分かる。
2.下図のような正十角形がある. 全体の面積が $1$ のとき,斜線部の面積を求めよ.
jmo2021y1
答え $\displaystyle \frac{2}{5}$
下図のように点を取る。ただし、点Oは正十角形の中心である。
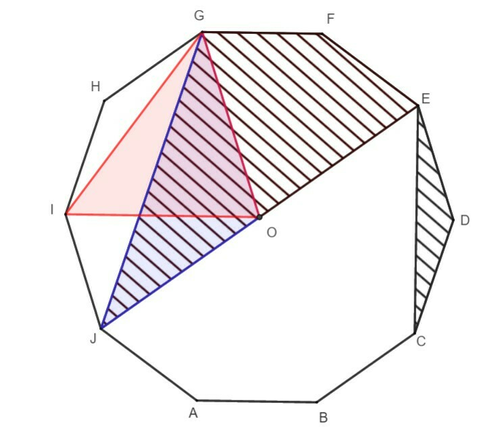jmo2021y1a
ここで、直線GOと直線IJは平行なので三角形GIOと三角形GJOの面積は等しい。また、明らかに三角形CDEと三角形GHIの面積は等しいので、求める面積は六角形EFGHIOの面積に等しい。これは正十角形の面積の $\frac{4}{10}$ であるから、求める面積は、$1\times \frac{4}{10}=\frac{2}{5}$ と分かる。
3.AB=ACなる二等辺三角形ABCの内部に点Pをとり、Pから辺BC,CA,ABにおろした垂線の足をそれぞれD,E,Fとする.BD$=9$,CD$=5$,PE$=2$,PF$=5$ のとき,辺ABの長さを求めよ.ただし,XYで線分XYの長さを表すものとする.
答え $4\sqrt7$
下図のように点を取る。ただし、点Jと点Gは線分BC上、点Kは線分AB上、点Lは線分AC上の点で、四角形FPJKと四角形EPGLはそれぞれ長方形である。また、BCの中点をMとする。
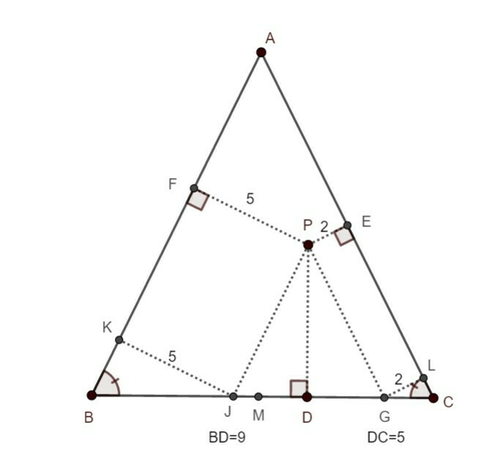jmo2021y3a
XYZで三角形XYZを表すことにする。
まず、ABM∽JBK∽PJD∽PGD∽GCL∽ACMである。
よって、BJ$=5x$とおけば、GC$=2x$ が分かる。さらに、JD$=$DGから、
$9-5x=5-2x$ を満たすので、$x=\frac{3}{4}$ が分かる。
次に三平方の定理からBK$=\frac{5\sqrt7}{3}$ が分かる。
BJ$:$BK=AB$:$BM から、$\frac{20}{3}:\frac{5\sqrt7}{3}=$ AB$:7$ となるので、AB$=4\sqrt7$ が分かる。
4.黒板に $3$ つの相異なる正の整数が書かれている.黒板に実数 $a,b,c$ が書かれているとき, それぞれを $\displaystyle \frac{b+c}{2},\frac{c+a}{2},\frac{a+b}{2}$ に同時に書き換えるという操作を考える.この操作を $2021$ 回行ったところ,最後に黒板に書かれた $3$ つの数はすべて正の整数だった.このとき,最初に書かれていた $3$ つの正の整数の和としてありうる最小の値を求めよ.
答え $3\times 2^{2021} + 3$
$3$ 実数が相異なれば、操作後の $3$ 実数も相異なることに注意する。
一般性を失わず、$a< b< c$ とし、$b-a=x>0,c-b=y>0$ とする。
このとき、$\frac{b+c}{2}=b+\frac{y}{2},\ \frac{c+a}{2}=b+\frac{y-x}{2},\ \frac{a+b}{2}=b-\frac{x}{2}$ より、$1$ 回の操作後の $3$ 数を $a',b',c'\ (a'< b'< c')$ とすると、$a'=b-\frac{x}{2},\ b'=b+\frac{y-x}{2},\ c'=b+\frac{y}{2}$ が分かる。よって、最初に黒板に書かれていた $3$ つの正の整数を $m-x,m,m+y\ (x,y>0)$ とすると、最後に黒板に書かれた $3$ つの数は、$m-\frac{x}{2^{2021}},\ m+(y-x)(1-\frac{1}{2^{2021}}),\ m+\frac{y}{2^{2021}}$ となる。これらはすべて正の整数であるから、$x\equiv y\equiv 0\ (\mod 2^{2021})$ が必要。さらに $m-x\ge1$ より、$m-x+m+m+y=3m+y-x\ge 2x+y+3$ (等号は $m=x+1$ で成立) となる。したがって、$x,y$ それぞれを最小化すればよく、$x=2^{2021},y=2^{2021}$ が分かる。$m=x+1=2^{2021}+1$ として、求める値は $3m+y-x=3\times 2^{2021} + 3$ となる。
