マンハッタン距離
はじめに
私はAtCoderなどの競技プログラミングを趣味でやっているのだが，その中の問題でマンハッタン距離に関するものが出題されることがある．（
D - Four Coloring
など）
そこでマンハッタン距離について調べて，簡単にまとめることにした．
距離空間
集合 $X$ と，関数$d:X\times X \rightarrow \R^+$に対し，関数 $d$が以下を満たすとき，$(X, d)$を距離空間という．（ただし，$\R^+ := \{x\in \R | x > 0\}$）
- $d(\boldsymbol{x}, \boldsymbol{y})=0 \Leftrightarrow \boldsymbol{x} = \boldsymbol{y}$
- $\boldsymbol{x},\boldsymbol{y}\in X$に対し，$d(\boldsymbol{x},\boldsymbol{y}) = d(\boldsymbol{y},\boldsymbol{x})$
- $\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}$に対し，$d(\boldsymbol{x},\boldsymbol{y}) + d(\boldsymbol{y},\boldsymbol{z}) \geq d(\boldsymbol{x},\boldsymbol{z})$
$d$を$X$上の距離ともいう.
$\boldsymbol{x_1}=(x_1, y_1)$，$\boldsymbol{x_2}=(x_2, y_2) \in \R^2$に対し，$ d(\boldsymbol{x_1},\boldsymbol{x_2}) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 }$と定めると，これは$\R^2$上の距離となる．
$d:\R^2 \times \R^2 \rightarrow \R$を$d(\boldsymbol{x_1},\boldsymbol{x_2}) =|x_1-x_2| + |y_1 - y_2|$をマンハッタン距離という．
距離になっていること
この$d$が$\R^2$上の距離になっていることを確認する．
- \begin{eqnarray} d(\boldsymbol{x_1},\boldsymbol{x_2}) =|x_1-x_2| + |y_1 - y_2| = 0 &\Leftrightarrow & |x_1 -x_2| = 0 \ \land \ |y_1 - y_2| = 0 \\ &\Leftrightarrow & x_1 = x_2 \ \land \ y_1 = y_2 \\ &\Leftrightarrow &\boldsymbol{x_1} = \boldsymbol{x_2} \end{eqnarray}
- $d(\boldsymbol{x_1},\boldsymbol{x_2}) =|x_1-x_2| + |y_1 - y_2| = |y_1-y_2| + |x_1 - x_2| = d(\boldsymbol{x_2},\boldsymbol{x_1})$
- \begin{eqnarray} d(\boldsymbol{x_1},\boldsymbol{x_3}) =|x_1-x_3| + |y_1 - y_3| & = & |x_1 - x_2 + x_2 - x_3| + |y_1 - y_2 + y_2 - y_3| \\ & \leq & |x_1 - x_2 | + |x_2 - x_3| + |y_1 - y_2 | + | y_2 - y_3| \\ & \leq & |x_1 - x_2 | + |y_1 - y_2 |+ |x_2 - x_3| + | y_2 - y_3| \\ & = & d(\boldsymbol{x_1},\boldsymbol{x_2}) + d(\boldsymbol{x_2},\boldsymbol{x_3}) \end{eqnarray}
図形的解釈
そもそも，この距離がなぜマンハッタン距離と呼ばれるかというと， マンハッタン の道路が四角く（日本人的に言えば碁盤目状）になっており，この道に沿って移動するときのことを考えるからである．
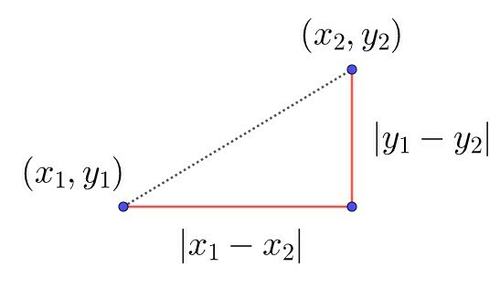マンハッタン距離
なお対角線（点線）が通常のユークリッド距離である．また，図から明らかなように，同一の点に対する（ユークリッド距離）$\leq$（マンハッタン距離）である．
将棋盤の上を縦または横にしか動けない状態で，何マス動けば目的のマスにたどり着けるかを考えていることを想像すれば少しは身近に感じられるかもしれない．
$\R^2$上の原点を$O$，$\R^2$上のユークリッド距離を$d_1$，マンハッタン距離を$d_2$とする．このとき$d_1(O,\boldsymbol{x_1}) < d_1(O,\boldsymbol{x_2})$かつ$d_2(O,\boldsymbol{x_1}) > d_2(O,\boldsymbol{x_2})$となるような$2$点$\boldsymbol{x_1}=(x_1,y_1)$，$\boldsymbol{x_2}=(x_2,y_2)$が存在するか．
（ユークリッド距離で測ると近く，マンハッタン距離で測ると遠くなるようなことがあるか）
解答例 例えば$(1,5)$，$(3,4)$が条件を満たしている．
座標変換
$45$度回転という操作について調べていると，マンハッタン距離との関連について書かれている記事が目に留まる．また，そこでは$(x,y) \rightarrow (x-y, x+y)$という座標変換について書かれている．そこでこの座標変換について考えてみることにする．
$A =
\left(
\begin{array}{rr}
1 & -1 \\
1 & 1 \\
\end{array}
\right)
$とすると，$A
\left(
\begin{array}{r}
x \\
y \\
\end{array}
\right)
=
\left(
\begin{array}{r}
x-y \\
x+y \\
\end{array}
\right)$となる．したがって，この行列$A$による線形変換を考える．$A=
\sqrt 2\left(
\begin{array}{r}
\cos \frac{\pi}{4} & -\sin \frac{\pi}{4}\\
\cos \frac{\pi}{4} & \sin \frac{\pi}{4}\\
\end{array}
\right)
$と書けることから，この線形変換は$\frac{\pi}{4}$回転して，$\sqrt 2$倍しているということがわかる．
$\left( \begin{array}{r} \cos \theta & -\sin \theta\\ \cos \theta & \sin \theta\\ \end{array} \right) $を角$\theta$の回転行列と呼んだりする．行列の積の計算方法と三角関数の加法定理や複素数平面のことを知っていれば，具体的に計算してみると納得できるはず．
次回へ
座標変換とマンハッタン距離の関連について書こうと思いましたが，記事が長くなりそうなので今回はここでいったん終了します．続きをまた書きたいと思います．
この記事を高評価した人
この記事に送られたバッジ
投稿者
