三平方の定理を忘れてしまった太郎くんが四平方の定理で正三角形の面積を求めるようです
三平方の定理を忘れてしまったら
問題．一辺の長さが1の正三角形の面積を求めよ
太郎くん（中３）「あれ…正三角形の面積ってどうやってもとめたらいいんだっけ…」
花子さん（中３）「三平方の定理をつかえばいいんだよ。ヘロンの公式や三角比の面積公式を使ってもいいね。」
太郎くん「うーん。三平方の定理忘れちゃったなあ。あ、でも$1:1:\sqrt2$の三角形はおぼえてるよ！」
花子さん「四平方の定理でも求められるけど…」
太郎くん「四平方の定理ならわかるよ！$a^2+b^2+c^2=d^2$だよね。」
花子さん「そうだね。$a,b,c,d$は3つの辺が直交してる四面体の各面の面積だね。」
太郎くん「$d$がどの面なのか、注意が必要だね！」
四平方の定理
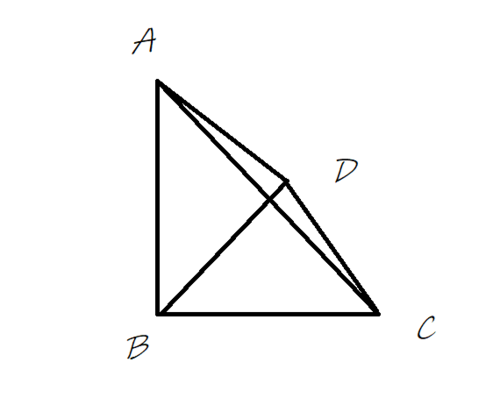四面体
$(ABC)^2+(ADB)^2+(BCD)^2=(ACD)^2$
ただし（ABC）で三角形ABCの面積とする。
証明は他サイトをご参照ください。
四平方の定理を使った正三角形の面積の求め方。
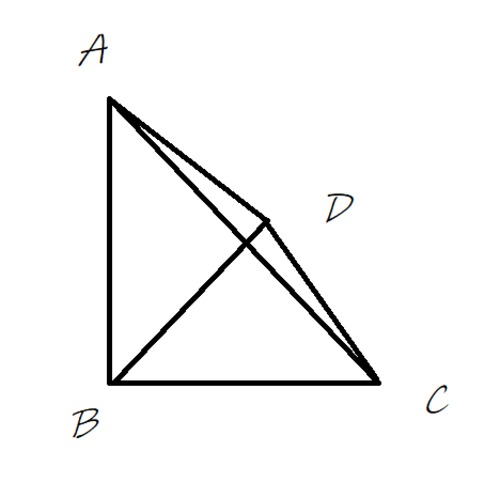四面体
$∠ABC=∠CBD=∠ABD=90°のとき、AB=BC=BD=\frac1{\sqrt2}$とすると、三角形$ACDは一辺が1の正三角形となる$。
四平方の定理より、$三角形ACDの面積(ACD)は
（ACD)^２=(ABC)^2+(BCD)^2+(ABD)^2$
なので、
$\sqrt{\frac{1}{16}・3}=\frac{\sqrt3}{4}$
よって一辺の長さが１の正三角形の面積は$\frac{\sqrt 3}{4}。$
太郎くん「やった！三平方の定理を忘れても正三角形の面積を求めることができたね！」
花子さん「入試までには三平方の定理も覚えようね…」
さいごに
「三平方の定理を覚えてない中学生がなんで四平方の定理を使えるんだ！！！」というツッコミはこらえてください。あまり触れられない四平方の定理ですが、もちろんながら既出だったものの過去に自分で見つけることができた定理なので実はお気に入りです。
誤植、ミス等があればコメント、twtterのDMでおしらせください。
自分の実力では書けるかわかりませんが、リクエスト受け付けてます。
この記事を高評価した人
この記事に送られたバッジ
投稿者
