ヘンテコな正三角形の定義とポンペイウの定理~「エレガントな解答をもとむ」との関連も~
いつだったかに思いついた正三角形の特徴づけについて書きます．我々がよく知る定義である$AB=BC=CA$と同値なことを見ましょう．
三角形$ABC$が正三角形である
$
\Longleftrightarrow
$$A,B,C$と共円でないどんな点$P$を取っても$PA,PB,PC$を三辺の長さとする三角形が常に存在する$ \cdots(\star )$
i ) $(\star )\Longrightarrow AB=BC=CA $
$BC$が最短辺であるとして一般性を失いません．両端を除く線分$BC$上の点$D$と$A$との距離の上限は$
\max \{AB,AC\}
$であり，$DA,DB,DC$が三角不等式を満たすとき$$DA \lt DB+DC=BC$$であることから$BC\geq \max \{AB,AC\}$が必要でこれは三辺の長さが等しいことを意味します．
ii ) $AB=BC=CA\Longrightarrow (\star ) $ (Pompeiu,1936)
三角形$ABC$の外接円周上にない任意の点$P$を取り，$A,P$を図のように$C$を中心に$60^\circ$回転させて得られる点を$A',P'$とします．
すると，三角形$PAP'$は$PA=PA,P'A=PB,PP'=PC$となり$(\star ) $を満たします．$\blacksquare $
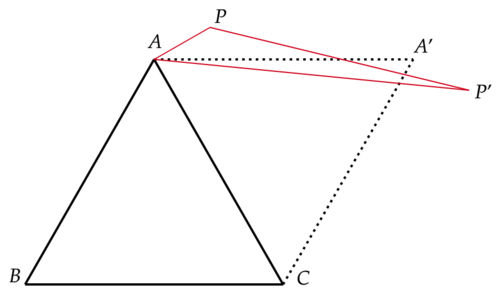diagram1
今回の話題ですが，なんともタイミングが良く，数学セミナーの看板コーナー「エレガントな解答をもとむ」にて 今井淳氏が2020年11月号に出題された問題 との関連があります．三角形の相似類のモジュライ空間を背景としているそうです．2021年2月号に解答が掲載されていますので気になる方は読んでみてください．
