自作問題解説
私がtwitterに載せた自作問題の解説です。
https://twitter.com/Gnu_yshys0624/status/1350051658206650373?s=20
角A=60°である三角形ABCで、角Aの二等分線と辺BCの交点をDとする。また、点Aを含む辺AB,AC上にそれぞれ点E,Fを角EDF=60°となるようにとる。AD=4のとき、線分EFが通りうる範囲の面積を求めよ。
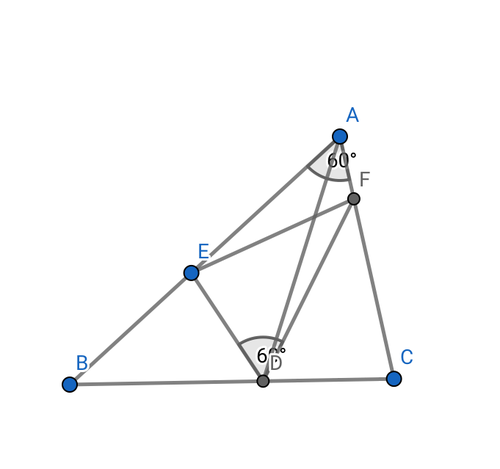 図
図
解説
解説に入る前に次のことを証明したいと思います。これがこの問題の核となります。
点Dは△AEFの点Aに対する傍心である-----*
証明:
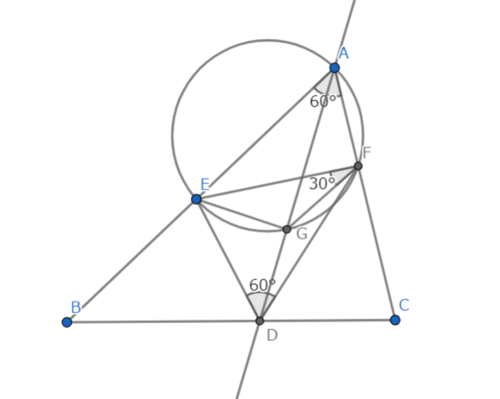 図2
図2
△AEFの外接円と直線ADとの交点のうち、点Aと異なる点をGとする。
四角形AEGFは円に内接するから、$\angle$EGF = 180° ー$\angle$EAF = 120°----①
また円周角の定理より$\angle$EFG = $\angle$EAG = 30°、同様に$\angle$FEG = 30°
よってEG = FGである。
このとき、①より$\angle$EGF = 2$\angle$EDF、またEG = FGより、点Gは△EDFの外心である。
ここで、$\angle$DFC = $\angle$DAF + $\angle$ADF = 30° + $\angle$GDF,
$\angle$DFE = $\angle$EFG + $\angle$GFD = 30° + $\angle$GDF
よって$\angle$DFC = $\angle$DFE
同様にして、$\angle$DEB = $\angle$DEF
よって、点Dは△AEFの点Aに対する傍心である ■
では問題の解答を書いていきます。点Dが△AEFの傍心であることに気づけば、あとは意外に単純です。
解答:
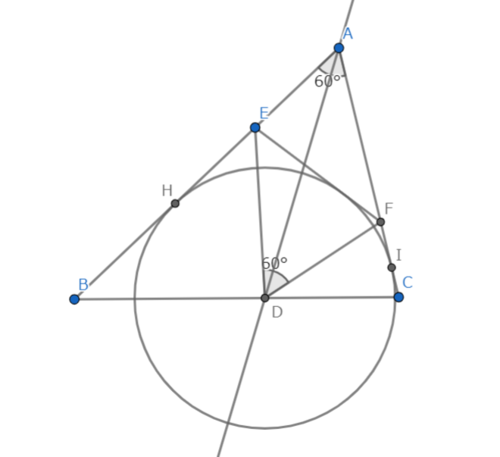 図3
図3
三角形AEFの点Aに対する傍接円を$\Gamma$とし、$\Gamma$とAB、ACとの接点をそれぞれ点H,Iとする。
このとき、*より線分EFは$\Gamma$と接しながら動くため、線分EFは四角形AHDIの扇形DIHを含めない部分を動く。
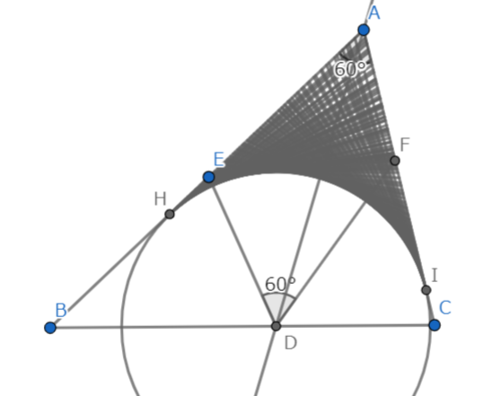 図4
図4
AD = 4より、求める面積は
2$\cdot$2$\sqrt{3}\cdot\frac{1}{2}\cdot2$ - $2^2\pi\cdot\frac{1}{3}$ = 4$\sqrt{3}$ - $\frac{4}{3}\pi$
となります。
