加群のグロタンディーク群（アティマク演習問題7.26解答）

加法的関数 $\lambda:F(A)\longrightarrow G$ に対して群準同型 $\bar{\lambda}:C\longrightarrow G$ を
$$\bar{\lambda}\left( \sum_{i}(-1)^{m_i}(M_i)\right)= \sum_{i}(-1)^{m_i}\lambda(M_i)$$
と定める。 このとき $D\subseteq \Ker(\lambda)$ なので準同型定理より

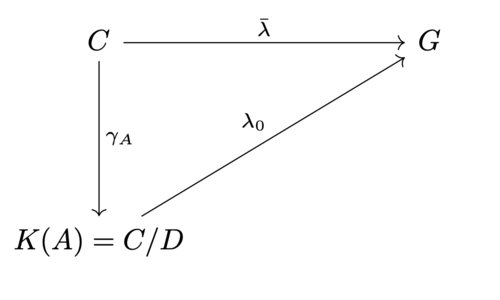
を可換にする $\lambda_0$ が $\bar{\lambda}$ に対してただ一つに定まる。$\bar{\lambda}$ は $\lambda$ に対してただ一つに定まるので、$\lambda_0$ も $\lambda$ に対して一意的に定まる。$\Box$

$M$ を任意の $F(A)$ の元とする。$M$ に対して命題１を適用すると
$$0=M_0\subset M_1\subset\cdots\subset M_r=M$$
が存在してある $A$ の素イデアル $\mathfrak{p}_i$ に対して
$$M_i/M_{i-1}\cong A/\mathfrak{p}_i$$
が各 $1\leq i\leq r$ に対して成り立つ。このとき、
$$0\longrightarrow M_{r-1}\longrightarrow M_{r}\longrightarrow M_r/M_{r-1}\longrightarrow 0$$
は完全列なので
$$\gamma_A(M)=\gamma_A(M_{r-1})+\gamma_A(M_r/M_{r-1})=\gamma_A(M_{r-1})+\gamma_A(A/\mathfrak{p}_r)$$
となる。同じことを $M_{r-1}$ にも施し、これを繰り返していくと
$$\gamma_A{M}=\sum_{i=1}^r\gamma_A(A/\mathfrak{p}_i)$$
が成り立つので、題意が示された。

$A$ は単項イデアル整域なので、$M\in F(A)$ は
$$M\cong A^r\oplus A/(e_1)\oplus \cdots\oplus A/(e_t)$$
という一意的な分解を持つ。ただし $e_i\in A,\,e_i|e_{i+1}$ である。したがって $\lambda:F(A)\longrightarrow \mathbb{Z}$ を $\lambda(M)=r$ として定めることができる。$\lambda$ が加法的関数であることを示そう。

$K$ を $A$ の商体とする。このとき
\begin{align*} K\otimes_A A/(e_i)&=(e_i\cdot e_i^{-1}K)\otimes_A A/(e_i)\\ &=( e_i^{-1}K)\otimes_A (e_i\cdot A/(e_i))\\ &=0,\\ K\otimes_A A^r&=K\otimes(A\oplus\cdots\oplus A)\\ &=(K\otimes A)\oplus\cdots\oplus (K\otimes A)\\ &=K^r \end{align*}
となるから $K\otimes M\cong K^{\lambda(M)}$ が成り立つ。$A$ は平坦 $A$-加群なので、その局所化である $K$ も平坦加群である。よって完全列 $0\longrightarrow M\longrightarrow N\longrightarrow L\longrightarrow 0$ に対して
$$0\longrightarrow K^{\lambda(M)}\longrightarrow K^{\lambda(N)}\longrightarrow K^{\lambda(L)}\longrightarrow 0$$
も完全列となる。したがってベクトル空間の次元公式から
$$\lambda(M)-\lambda(N)+\lambda(L)=0$$
が成り立ち、$\lambda$ が加法的関数であることが示された。

したがって問題１で示した普遍性により $\lambda(M)=\lambda_0(\gamma_A(M))$ を満たす $\lambda_0:K(A)\longrightarrow \mathbb{Z}$ が存在する。$\lambda$ が $F(A)$ から $\mathbb{N}$ への全射になっているので $\lambda_0$ の全射性は明らかである。また、$0\neq e\in A$ に対して
$$0\longrightarrow A\longrightarrow A\longrightarrow A/(e)\longrightarrow 0$$
は完全列である。ただし左から２つ目の射は $e$ 倍写像である。よって $\gamma_A(A/(e))=\gamma(A)-\gamma(A)=0$ となるから $\lambda(M)=0$ のとき
$$M\cong A/(e_1)\oplus \cdots\oplus A/(e_t)$$
より $\gamma_A(M)=0$ が成り立つので $\lambda_0$ は単射である。以上により $K(A)\cong\mathbb{Z}$ が示された。$\Box$

$\pi:F(B)\longrightarrow F(A)$ をスカラーの制限とすると、$\pi$ によって完全列は完全列へと移されるので $\gamma_A\circ \pi$ は $F(B)$ から $K(A)$ への加法的関数である。したがって普遍性から $f_!$ が題意の条件を満たすように定まる。

図式

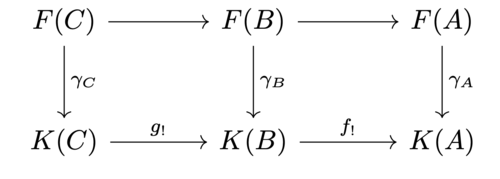
を考える。問題１で示した普遍性により２つの穴の部分は可換となり、したがってこの図式は全体としても可換となる。また、同様に普遍性から図式

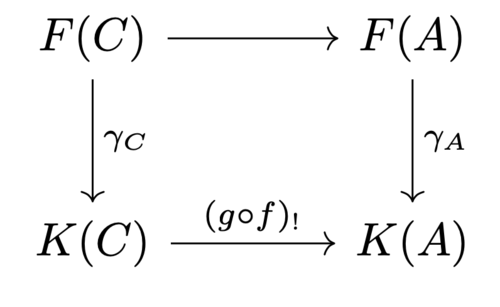
も可換となる。この図式におけるスカラーの制限 $F(C)\longrightarrow F(A)$ は合成射 $F(C)\longrightarrow F(B)\longrightarrow F(A)$ に等しいから二つの図式の可換性から
$$f_!\circ g_!\circ \gamma_C=(g\circ f)_{!}\circ\gamma_C$$
となる。したがって
$$f_!\circ g_!=(g\circ f)_{!}$$
を得る。$\Box$