正五角形と正十二面体と・・・!?
この記事は、令和2年度大学入学共通テスト数学ⅡB第5問にインスパイアされました。
ネタバレを含むので、これから解きたいという人はまず自力で解いてからこの記事を読んでください。
正五角形
一辺が$1$の正五角形$OA_1B_1C_1A_2$を考えます。この対角線の長さを$\phi$とします。原文では$a$ですが、$\phi$の方が一般的にはよく使われているので$\phi$を使用します。
($a$にしたのはたぶんマークシートに「φ」がなかったからだと思います)
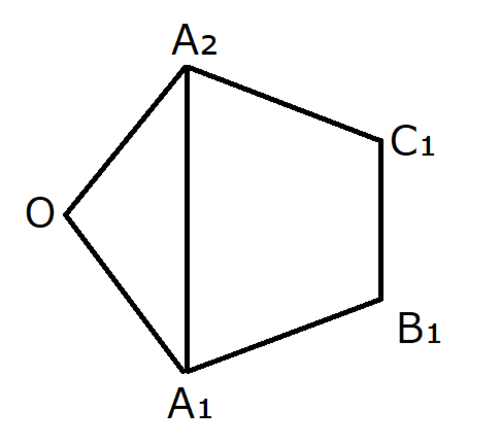 正五角形
正五角形
単に「$\phi = \frac{1+\sqrt{5}}{2}$である。」で終わらせてもいいのですが、原文では私の見たことのない方法で求めていたので省略せずに紹介します。
そのために、$\vector{B_1C_1}$を2通りの方法で表します。
$\vector{B_1C_1} = \frac{1}{\phi} \vector{A_1A_2} = \frac{1}{\phi}\left(\vector{OA_2} - \vector{OA_1} \right)$
$ \begin{align*} \vector{B_1C_1} &= \vector{B_1A_2} + \vector{A_2O} + \vector{OA_1} + \vector{A_1C_1} \\ &= -\phi\vector{OA_1} - \vector{OA_2} + \vector{OA_1} + \phi{OA_2} \\ &= (\phi - 1)\left( \vector{OA_2} - \vector{OA_1} \right) \end{align*} $
ここから、
$$ \frac{1}{\phi} = \phi - 1 $$
すなわち
$$ \phi = \frac{1+\sqrt{5}}{2} $$
が得られます。
原文では2つ目の$ \vector{B_1C_1} $の係数の$ \phi - 1 $だけ求めさせて、問題文中に「$ a = \frac{1+\sqrt{5}}{2} $を得る。」と書いてしまっています。黄金比を知らない人のための救済措置かもしれませんね。
後のために、$\vector{OA_1} \cdot \vector{OA_2}$を計算しておきます。
$$ \left|\vector{A_1A_2}\right|^2 = \phi^2 = \phi+1 $$
であるから
$ \begin{align*} \left|\vector{OA_2} - \vector{OA_1}\right|^2 &= \left|\vector{OA_2}\right|^2 + \left|\vector{OA_1}\right|^2 - 2 \vector{OA_2} \cdot \vector{OA_1} \\ 2 \vector{OA_1} \cdot \vector{OA_2} &= 1 + 1 - (\phi + 1) \\ 2 \vector{OA_1} \cdot \vector{OA_2} &= 1 - \phi \\ \vector{OA_1} \cdot \vector{OA_2} &= \frac{1}{2} - \frac{1}{2}\phi \end{align*} $
が求まります。ベクトルの内積は可換(入れ替えても結果が同じ)であることに注意しましょう。
正十二面体
正十二面体について復習しましょう。正十二面体の定義は、原文に書いてあります。
正十二面体とは,どの面も全て合同な正五角形であり,どの頂点にも三つの面が集まっているへこみのない多面体のことである。
正確に描くのは難しいですが、問題に必要な分はこれだけです。
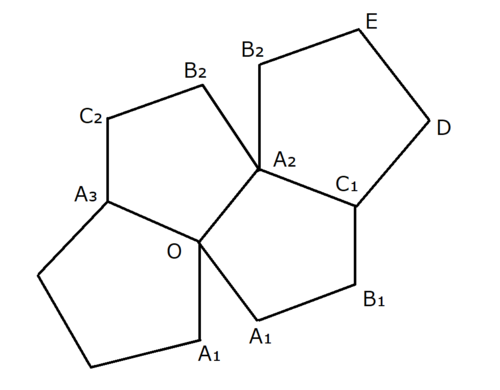 正十二面体(の展開図)の一部
正十二面体(の展開図)の一部
この図形は実際には3次元的に折れ曲がっていて、2つの$A_1, B_2$は実はそれぞれ同じ点であることに注意しましょう。
$O$から見ると$A_1, A_2, A_3$は対称なので(実際には3次元的に折れ曲がっているので$A_1$の隙間はないのです)、
$$ \vector{OA_1} \cdot \vector{OA_2} = \vector{OA_2} \cdot \vector{OA_3} = \vector{OA_3} \cdot \vector{OA_1} = \frac{1}{2} - \frac{1}{2}\phi $$
が成り立ちます。つまり、
$\begin{align*} & \vector{OA_1} \cdot \vector{OB_2} \\ &= \vector{OA_1} \cdot \left( \vector{OA_3} + \phi\vector{OA_2} \right) \\ &= \vector{OA_1} \cdot \vector{OA_3} + \phi \vector{OA_1} \cdot \vector{OA_2} \\ &= ( 1 + \phi )\left( \frac{1}{2} - \frac{1}{2}\phi \right) \\ &= -\frac{1}{2}\phi^2 + \frac{1}{2} \\ &= -\frac{1}{2}(\phi + 1) + \frac{1}{2} \\ &= -\frac{1}{2}\phi \end{align*}$
となります。また、
$\begin{align*} & \vector{OA_2} \cdot \vector{OB_2} \\ &= \vector{OA_2} \cdot \left( \vector{OA_3} + \phi\vector{OA_2} \right) \\ &= \vector{OA_2} \cdot \vector{OA_3} + \phi \vector{OA_2} \cdot \vector{OA_2} \\ &= \left( \frac{1}{2} - \frac{1}{2}\phi \right) + \phi \\ &= \frac{1}{2}\phi + \frac{1}{2} \end{align*}$
なので、
$\begin{align*} & \vector{OB_1} \cdot \vector{OB_2} \\ &= \left( \vector{OA_2} + \phi\vector{OA_1} \right) \cdot \vector{OB_2} \\ &= \vector{OA_2} \cdot \vector{OB_2} + \phi \vector{OA_1} \cdot \vector{OB_2} \\ &= \left( \frac{1}{2}\phi + \frac{1}{2} \right) + \phi\left( -\frac{1}{2}\phi \right) \\ &= \frac{1}{2}((\phi + 1) - (\phi + 1)) \\ &= 0 \end{align*}$
となり、$\angle B_1OB_2$が直角であることが分かります。
ここで、四角形$OB_1DB_2$について考えると、$OB_1=OB_2=B_2D=\phi$、$\angle B_1OB_2$が直角、$B_2D$は図上では$OB_1$と平行で実際には$A_2C_1$を固定したまま3次元方向に回転するだけなので3次元でも平行となります。このような条件を満たす2次元図形は正方形しかないので、四角形$OB_1DB_2$は正方形なのです!
正百二十胞体
ここで終わるのは面白くないですね。もう1つ次元を上げて、ヨジゲンパワーを感じましょう。※これは怪しい記事ではありません
正百二十胞体を、上の正十二面体の説明に沿って書くと、次のようになります。
正百二十胞体とは,どの胞も全て合同な正十二面体であり,どの頂点に四つの胞が集まっているへこみのない多胞体のことである。
さて、正五角形に長さ$\phi$の線分、正十二面体に一辺$\phi$の正方形があったことを考えると、正百二十胞体には一辺$\phi$の立方体がありそうですね。
一辺$\phi$の正方形の各辺は正五角形内の長さ$\phi$の線分なので、一辺$\phi$の立方体の各面は正十二面体内の一辺$\phi$の正方形になっていそうです。
...というか、正十二面体の中に立方体がすでにあります。 WikipediaのAnother Mattさんによる図 をお借りします。
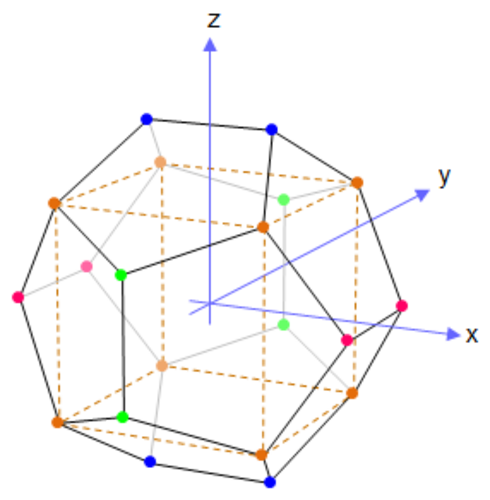 正十二面体の頂点
正十二面体の頂点
元の問題は、この上面だけを取り出したのですね。
では、正百二十胞体の中には超立方体があるのでしょうか。
Python3とかWolfram|Alphaとかもろびとこぞりて座標を計算してみましたが、正十二面体のときとは違ってかなりつらそうです。
どころか、超立方体の一辺が2つの正十二面体にまたがるようで、こうなるともう非常に繁雑な計算が必要となります。
WikipediaのTetracubeさんによる図 をお借りします。
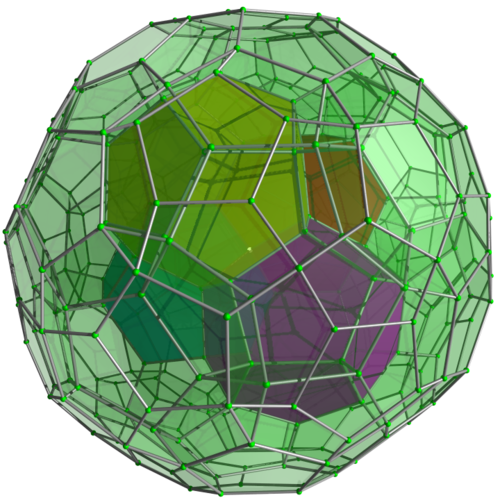 正120胞体
正120胞体
どうやら超立方体の一辺はここのような気がするのですが、証明できませんでした。。。
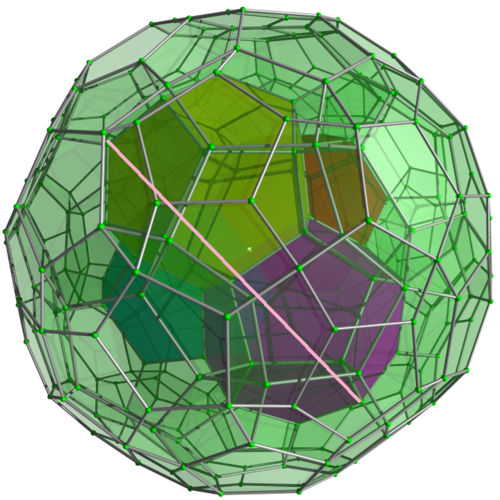 超立方体の一辺???
超立方体の一辺???
筆者はここで体力が尽きてしまいました。「その線じゃないよ!」とか「証明出来た!」とか何かわかった方はコメント欄で教えてください。
だって、