三平方の定理を忘れてしまった太郎くんが五平方の定理を使って正四面体の体積を求めるようです

Mathlog

三平方の定理を忘れてしまったら　其の二

※この記事では五平方の定理は以下で説明するものとします。

五平方の定理

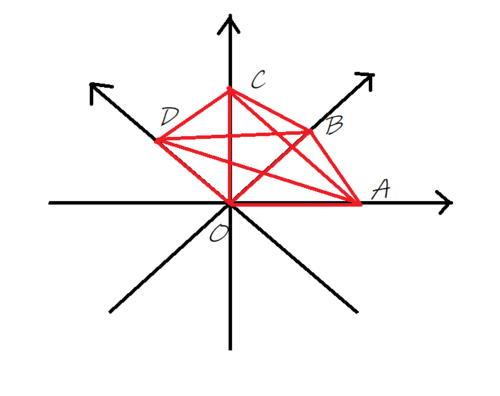五胞体
四本の軸がそれぞれ一点$O$で直交しているとき、四本の各軸上に四点$A（a,0,0,0）,$$B(0,b,0,0),$$C(0,0,c,0),$$D(0,0,0,d)$をとる。
このとき四面体$OABC,OABD,OACD,OBCD,ABCD$において、
$|OABC|^2+|OABD|^2+|OACD|^2+|OBCD|^2=|ABCD|^2$
が成り立つ。ただし$|ABCD|$で四面体$ABCD$の体積とする。

証明

証明の作成はみゆさん(＠dqx_miyu)にお手伝いしていただきました。

この証明内では高校数学と四平方の定理は既知のものとします。
$AB$で$AB$の距離、$|ABC|$で三角形$ABC$の面積、$|ABCD|$で四面体$ABCD$の体積とします。
$A,B,C,DをA（a,0,0,0）,B(0,b,0,0),C(0,0,c,0),D(0,0,0,d)$とする。(a$,b,c,d$はそれぞれ正)
四面体$OABC,OABD,OACD,ABCD$の体積はそれぞれ
$|OABC|=\frac{abc}{6},\ |OABD|=\frac{abd}{6},\ |OACD|=\frac{ACD}{6},\ |OBCD|=\frac{BCD}{6}$
四平方の定理より
$\begin{eqnarray}|ABC|^2 &=& \left(\frac{ab}{2}\right)^2+\left(\frac{bc}{2}\right)^2+\left(\frac{ca}{2}\right)^2 \\ &=& \frac{a^2b^2+b^2c^2+c^2a^2}{2^2}\end{eqnarray}$
三点$A,B,C$を通る面の方程式は、切片方程式より
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\\ bcx+cay+abz−abc=0$
この平面から原点までの距離は、
$\frac{|abc|}{\sqrt{(ab)^2+(bc)^2+(ca)^2}}=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}$
となることがわかります。これは、原点から$A,B,C$に下した垂線と$A,B,C$を通る面の交点を$M$とすると、
$OM=\frac{abc}{\sqrt{(ab)^2+(bc)^2+(ca)^2}}$
$OM$と$OD$は$O$で直交しているので、
$\begin{eqnarray}(MD)^2&=&\frac{a^2b^2c^2}{a^2b^2+b^2c^2+c^2a^2}+d^2\\ &=&\frac{a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2}{a^2b^2+b^2c^2+c^2a^2} \end{eqnarray}$
となり、これは底面を三角形$ABC$としたときの四面体$ABCD$の高さとなる。
$\begin{eqnarray} |ABCD|^2 &=& \frac{1}{3^2}・|ABC|^2・(MD)^2 \\ &=& \frac{1}{3^2}・\frac{a^2b^2+b^2c^2+c^2a^2}{2^2}・\frac{a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2}{a^2b^2+b^2c^2+c^2a^2}\\　&=& \frac{a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2}{6^2}\\ &=& \left(\frac{abc}{6}\right)^2+\left(\frac{abd}{6}\right)^2+\left(\frac{acd}{6}\right)^2+ \left(\frac{bcd}{6}\right)^2　\ \ \ \ □ \end{eqnarray}$

正四面体の体積の求め方

問題.　一辺が1の正四面体の体積を求めよ

$OA=OB=OC=OD=\frac{1}{\sqrt2}$とすると、
$四面体ABCDはAB=AC=AD=BC=BD=CD=1$の正四面体になる。
$|OABC|=|OABD|=|OACD|=|OBCD|=\frac{1}{12\sqrt{2}}$
五平方の定理より、
\begin{eqnarray}|ABCD|^2 &=& 4・\left(\frac{1}{12\sqrt{2}}\right)^2\\ &=& \frac{1}{72}\\ |ABCD|&=&\frac{\sqrt2}{12} \end{eqnarray}

さいごに

今回五平方の定理の証明の作成でお手伝いしていただいたみゆさん( Mathlog / twitter )
みゆさん本当にありがとうございました。

共通テストも一段落して太郎くんと花子さんの旬が過ぎた気もしなくもないですが、今回も登場してもらいました。次回は未定です。

誤植、ミス等があればコメント、twtterのDMでおしらせください。
自分の実力では書けるかわかりませんが、リクエスト受け付けてます。